-- Вы знаете, Адам, новость -- на каждого гражданина
давит столб воздуха силою в двести четырнадцать кило!
-- Нет, -- сказал Козлевич, -- а что?
-- Как что! Это научно-медицинский факт.
И мне это стало с недавнего времени тяжело.
Вы только подумайте! Двести четырнадцать кило!
Давят круглые сутки, в особенности по ночам.
Ильф и Петров, Золотой теленок
Бывают такие вопросы, что их даже задавать как-то странно. Например, почему реакция опоры N = mg. Если человек посещал уроки физики и занимался на них физикой, а не общением в соцсетях и подъемом своего lvl'а, он как минимум ответит -- по III закону Ньютона. И ошибется, причем подобная ошибка, даже если само уравнение написано правильно, обойдется ему на ЕГЭ в один сырой тестовый балл, то есть в два, а может быть, даже и в три тех баллов, за которые он, собственно, борется. Потому, что третий закон говорит о силах, приложенных к разным телам, а N и mg приложены к одному. Более внимательный школьник ответит правильнее -- по II и III законам, и даже проделает соответствующий вывод. Школьник, который еще более дотошен, сумеет получить соотношение между N и mg, если опора сама имеет ускорение a. Впрочем, и его можно запутать, спросив, что будет, если у опоры ускорение направлено вниз и a > g.
Воспользовавшись его растерянностью, сообщим, что физика отличается от математики тем, что в ней ни одна задача не может быть решена до конца. Потому, что она -- одна из так называемых естественных наук, то есть наука, непосредственно относящаяся к природе, рассматривающая процессы, происходящие или предположительно происходящие в природе. Кстати, математика тоже частично относится к природе, но опосредовано, через естественные науки. А реальные физические задачи могут быть решены только для некоторых условий и с некоторой точностью. Если же мы изначально оговорим, какие законы считаем соблюдающимися и договоримся пренебрегать всем остальным, то есть сведем физику к некоторой ограниченной модели, то тогда станут возможны точные и окончательные решения. Именно так мы всегда поступаем в школе с физикой и химией, создавая не вполне правильное представление о науках. Обратимся к нашей конкретной задаче про N и про mg.
Вот вопрос, который должен возникать -- почему при выводе пресловутого N = mg мы не учитываем давления воздуха P? И не вздумайте что-то говорить про "мало" и "пренебрегаем" -- сила, с которой воздух на Земле -- если не лезть в горы, -- давит на поверхность, составляет около 10 Н/см2 или около 2000 Н вертикально сверху на стоящего и 20000 Н на горизонтально лежащего человека (Остап Бендер явно знал школьную физику). Напоминаю, что 2000 и 20000 Н -- это вес массы в 200 кг и 2000 кг соответственно. То есть, когда вы спите, на вас стоит примерно половина слона или два медведя -- как вам больше нравится.
В школьном учебнике рассматривается вопрос о механических напряжениях в твердом теле, жидкости и газе, и в хорошем учебнике даже объяснено, почему напряжения в газе и жидкости называют давлением. Конечно, это надо было бы сделать яснее, обсудив применимость понятия "давления" для разных случаев, но сейчас речь не об этом, а о том, почему мы не учитываем силу Архимеда при выводе N = mg? Ответ на вопрос известен -- потому, что воздух примерно на три порядка легче воды, а металлов -- примерно на четыре. Тут еще можно вспомнить старую шутку про килограмм гвоздей и килограмм ваты, и попросить дать численную оценку. Кстати, при попытке это сделать часто забывают, что "истинный объем" ваты -- тот, который должен войти в силу Архимеда, -- сильно отличается от геометрического, внешнего объема, от, так сказать, объема подушки.
Упоминание закона Архимеда для тел, мирно спящих на аэродромах, то есть лежащих на столах, может -- и должно! -- было бы указать читателю на ключевой момент. А именно, на давление атмосферы на нижнюю плоскость. Именно поэтому в великое уравнение N = mg не входит PS. Вместо него должен был бы входить закон Архимеда, которым, как правило, пренебрегают. Потому, что в учебнике физики Архимед всплывает позже реакции опоры, а применять одно утверждение курса к другому, которое было раньше -- слишком сложное требование.
Однако наши приключения только начинаются. Прежде всего, стоит спросить, глубока ли и широка ли щель -- та, которая имеется под мирно спящем на столе телом. Это зависит от механическах свойств и рельефа поверхности соприкасающихся тел. Когда мы кладем реальное шероховатое тело, то сначала оно касается одной точкой, потом, чуть повернувшись, второй, потом еще чуть повернувшись, третьей, а еще чуть опускается, расширяя площади так называемого "истинного контакта" вокруг этих точек, причем итоговая суммарная площадь всех контактных площадок должна быть такой, чтобы материал выдерживал вес верхней. Заметим, что при соприкосновении могли возникнуть еще контактные области, кроме первых трех. И что деформировалось оба тела, причем распределение деформаций зависело характеристик шероховатости и твердостей обоих поверхностей.
Если мы кладем, например, стальной куб с ребром 10 см, масса которого примерно 8 кг, а вес -- 80 Н, на стальную поверхность, то площадь истинного контакта при прочности материала 50 кг/мм2 (5·108 Н/м2) составит, как легко посчитать 0,16 мм2. Это ничтожно малая доля -- 16 миллионных! -- от "геометрической площади контакта", которая составляет 10000 мм2. Ситуация, когда площадь истинного контакта составляет малую долю от "геометрической", является для техники постоянной и вездесущей. И она влечет множество разных проблем. Например, если через контакт нужно передавать тепло или электрический ток, им приходится протискиваться через эти маленькие пятнышки. При передаче тепла это влечет увеличение перепада температур между деталями (или при фиксированном перепаде температур -- уменьшение потока. При протекании электрического тока маленькие контактные площадки из-за высокой плотности тока в них перегреваются, контакты могут свариваться, могут плавиться, даже испаряться. И это еще только начало проблем. Например, именно поведением контактов определяет сухое трение и химические процессы, идущие на контакте твердых тел.
Но сейчас нас интересует щель под телом, которое лежит. Для твердых материалов оная щель, как мы уже понимаем, занимает почти все пространство под телом. Про мягкие тела поговорим чуть позже, а сейчас вопрос -- как у этой щели дела с толщиной, пролезет ли туда молекула? Оптические поверхности имеют идеальную поверхность с точностью 0, 1-0,01 ? -- то есть от 1/10 до 1/100 длины волны видимого света, от 50 до 5 нм. Это чудовищно мало: если учесть, что при нормальном давлении расстояние между молекулами в газе порядка 3 нм, то если мы приведем в соприкосновение такие поверхности, в щели по ширине смогут расположиться от 20 до 2 молекул. Однако этого вполне достаточно для давления -- молекулы мечутся, как безумные, за секунду сталкиваясь со стенками от 6 до 60 миллиардов раз и благополучно передают им импульс. Попутно заметим, что в некотором смысле (например, для движения вдоль щели) они ведут себя, как при "высоком вакууме" -- они сталкиваются в основном со стенками, а не друг с другом.
Кстати, когда в книгах заводят речь о диффузии в твердых телах, разговор начинают с того, что надолго прижимают свинец к золоту, а потом изучают, проникли ли атомы золота в свинец и наоборот. Но почему берут именно эти металлы? От каких свойств металлов зависит количество проникших атомов? В частности, от тех, от которых зависит площадь истинного контакта, площадь "пятнышек". А она тем больше, чем металл тяжелее (если он просто лежит, а не прижат дополнительной силой) и от твердости. Мягкий металл прижимается плотнее, по большей площади.
А что произойдет, если одно из веществ настолько мягкое, что площадь истинного контакта оказывается сравнимой с "геометрической"? Тогда тела прижимаются друг к другу весьма большими силами атмосферного давления, и рассоединить их должно быть трудно. Почему же нам легко удается отделить от стола прижатую к нему резинку? Ответ -- потому что она вся мягкая, при прижатии она деформируется вся, отчасти распластывается, и отделяем мы ее понемногу, плавно уменьшая геометрическую площадь контакта, а не всю сразу. Вот если бы мы сделали жесткую деталь с тонким мягким покрытием, и прижали этим покрытием к жесткой поверхности, отделить ее от этой поверхности стало бы труднее. Например, говорят, что подводную лодку может "присосать" к дну. Это образное описание эффекта, возникающего при таких характеристиках грунта, что корпус плотно прилегает к нему, вода из щели вытесняется, а давление сверху остается (в воде на глубине 10 м уже 10 тонн/м2).
Теперь мы перенесемся в далекое прошлое, в конец позапрошлого века. Жил да был в Швеции инженер Карл Эдвард Йоханссон, и придумал он в 1896 году новый способ создания эталонных размеров. Странное словосочетание, правда? Дело в том, что для высокоточного измерения размеров очень полезно иметь какие-то эталоны, то есть что-то, имеющее точно известный размер. Придумал он следующее -- выпускать наборы пластинок, очень точной длины, причем обработанных так, чтобы две пластинки, если их плотно прижать друг к другу и слегка сдвинуть одну по другой, "притереть", как принято говорить в технике, -- слипались. На фото показаны две "плитки Иогансона" в 30 и 40 мм, которые держит автор этой статьи.

О создателе этих плиток и истории создания вы легко найдете информацию в Интернете. Просто спросите Гугла "плитки Иогансона", а лучше "gauge Johansson". Карл Эдвард прекрасно понимал, какую замечательную вещь он придумал, запатентовал и выпускает -- посмотрите хотя бы на эмблему его фирмы.
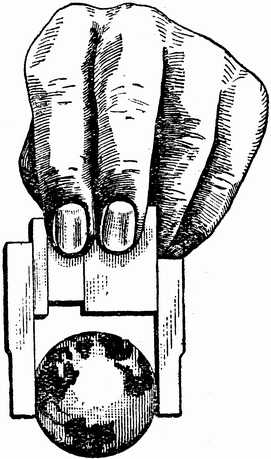
Делал он их, понятное дело, из стали. Нынче выпускают и стальные, и из карбида вольфрама, и из керамики. У всех материалов свои преимущества: стальные дешевле, карбид вольфрамовые меньше истираются при использовании, а у керамических меньше тепловое расширение.
Забавно, что за все эти годы как-то никто и не разобрался, почему они слипаются. В основном произносятся слова про ван-дер-ваальсовы силы и про поверхностное натяжение. Поверхностное натяжение может удержать на воде водомерку и иголку, но не стограммовую железку на весу, а для того, чтобы "заработало" межмолекулярное притяжение, поверхности должны сблизиться на межатомное расстояние, причем по всей площади. В зарубежных источниках, правда, упоминается атмосферное давление, но лишь как один из факторов, и не главный.
Плитки Иогансона (в эпоху борьбы с "низкопоклонством перед Западом" их переименовали в "концевые меры") прижимает друг к другу именно атмосферное давление, а ничтожного количества влаги (и, возможно, масла), всегда имеющегося на поверхности, оказывается достаточно, чтобы не пустить в щель атмосферу. А если качество поверхностей немного хуже, на них приходится подышать -- понятно зачем?
Но этим дело не кончается, это только первый слой задачи. Атмосферное давление на вертикальные поверхности действует горизонтально, а гравитация -- как обычно, вертикально. Поэтому, чтобы удержать плитку от падения, нужен коэффициент трения -- сухого трения. Однако в упрощенной модели мира трение бывает только или сухое, или по жидкой смазке. Реальная ситуация может быть сложнее, например, когда машина едет по мокрой мостовой, реализуется смешанное трение -- вода успевает (хорошо, если успевает) выдавиться из зоны контакта (и долететь до прохожих), а когда мы "притираем" плитки, мы как раз и выдавливаем воду с некоторых участков. На которых реализуется непосредственный контакт плиток и то самое сухое трение. Поэтому вода с одной стороны, не пускает атмосферу в щель, а с другой -- не исключает сухого трения на некоторых участках.
Однако и это еще не все. Вода или иная жидкость, заполняющая зазор, контактирует с атмосферой и в ней, казалось бы, все равно должно быть атмосферное давление. Например, в воде на глубине 10 м или в ртути на глубине 760 мм давление не 1 атм, а 2 атм -- мы об этом иногда забываем, причем не когда ныряем, а, к сожалению, на экзамене. Но тут и приходит на помощь поверхностное натяжение, то самое, которое поднимает жидкость в капиллярах. Раз жидкость в капилляре оказывается выше исходного уровня -- значит, давление в ней уменьшается. Высота поднятия обратно пропорциональна зазору, и, когда он уменьшается до единиц микрон, давление в жидкости становится существенно меньше атмосферного. Вода в микрозазоре между плитками ведет себя как в капилляре -- то есть тоже образует мениск, под которым понижено давление. Поэтому, кстати, плитки Иогансона будут слипаться и в вакууме! Потому что хотя атмосферного давления там нет, но есть отрицательное давление в жидкости.
Итак, чтобы происходило то, что вы видите на фото, нужно соблюдение трех условий. Неплоскостность поверхностей должна быть не более единиц микрометров -- чтобы не было больших зазоров, в которых вода, если и будет присутствовать, не сможет защитить плитки от атмосферного давления. Должно оказаться на поверхности потребное -- ничтожное! -- количество влаги и, возможно, масла -- кстати, в реальной жизни протирка бензином вовсе не очищает поверхность полностью. Наконец, плитки должны быть отполированы так, чтобы при прижатии с силой в несколько килограмм (притирании) образовалась зона непосредственного контакта. На ней, между прочим, могут позволить себе начать действовать и ван-дер-ваальсовы силы, хотя атмосферное давление и будет превосходить их на один-два порядка.
В самом начале этой статьи говорилось, что если мы при решении задач сразу оговорим, какие законы будем считать соблюдающимися и будем пренебрегать всеми остальным, то сможем получать точные и окончательные решения. Однако нам может попасться -- в реальной работе или на экзамене -- задача, которую не удастся решить в такой ограниченной модели. В реальной работе это совершенно нормальная ситуация, и это означает, что надо расширять модель. Получение же такой задачи на серьезном экзамене (на ЕГЭ таких задач не может быть) означает, что экзаменатор хочет проверить именно нашу способность решать реальные задачи, расширять модели, то есть заниматься настоящей наукой. Впрочем, такую задачу могут дать и чтобы попросту "завалить".
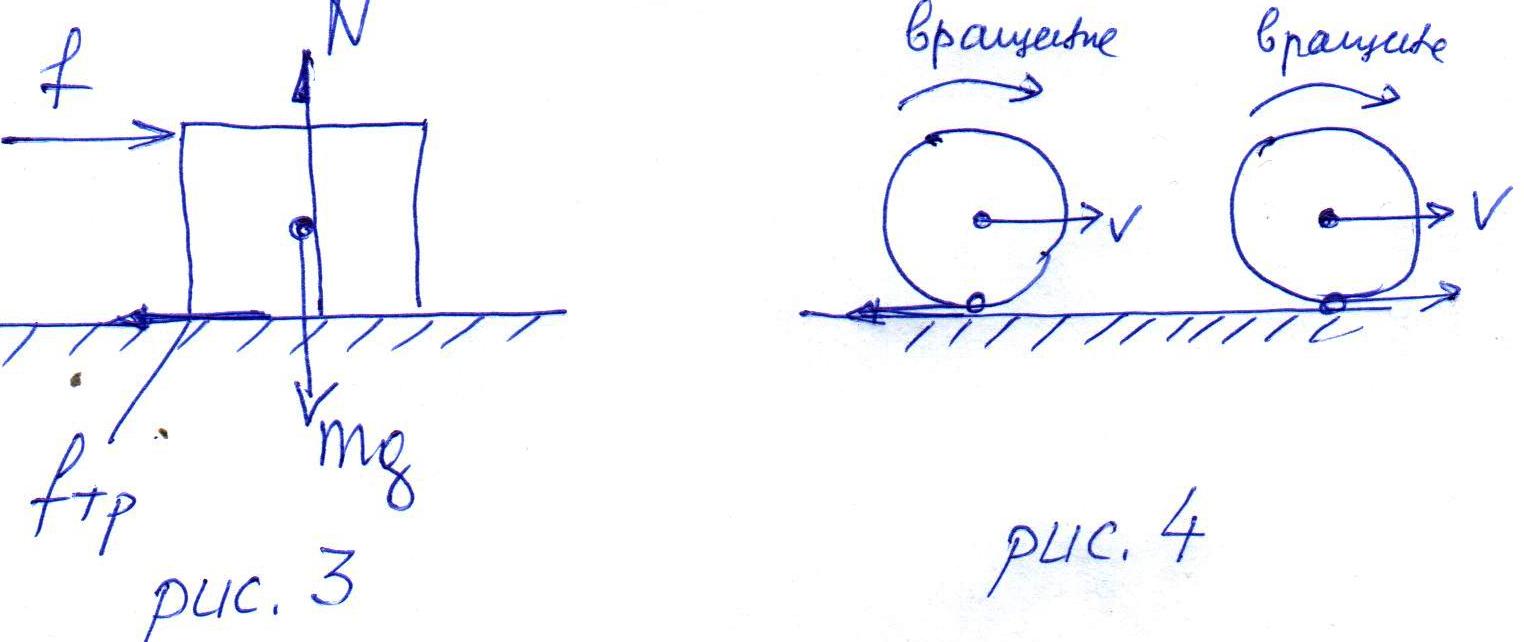
Вот два примера задач, связанных с реакцией опоры, которые можно решить, только "расширяя" модель. Пусть на поверхности лежит кубик, и к его верхней точке приложена горизонтальная сила (рис. 3). Если все силы изображены так, как показано на рисунке, налицо противоречие -- сумма сил ноль, но суммарный момент не равен нулю! Кубик обязан начать вращаться. Немного подумав, мы поймем, что с тремя из этих сил мы не можем сделать ничего такого, что повлияло бы на создаваемый ими момент. Единственное, что может нас спасти -- сдвиг реакции опоры вправо. А почему, собственно, мы всегда рисуем ее проходящей через центр тяжести? Подсказка -- представьте себе, что кубик лежит на мягкой поверхности. Что произойдет, если мы приложим к его верхней точке горизонтальную силу?
Кубик промнет под собой поверхность, причем неравномерно -- правый угол опустится ниже левого. Это означает -- согласно закону Гука -- что давление на опору станет распределено по плоскости неравномерно, на правом конце оно будет больше, чем на левом (рис 5 слева). Суммарная сила реакции опоры окажется сдвинутой вправо, что и требуется для поддержания отсутствия вращения. Заметим, что мы сейчас слегка вышли за обычный курс и, по существу, прибегли к понятию распределенной силы. На самом деле для тел, имеющих размеры (не для материальных точек) многие силы являются распределенными, например, трение, реакция опоры, гравитация. Но при решении школьных задач это обычно игнорируется.
Вторая задача: по горизонтальной поверхности катится шарик. Он понемногу тормозится и в итоге, как ему и положено, останавливается. Как была направлена сила трения, которую называют "сила трения качения"? Если назад (рис. 4 слева), то шарик будет тормозиться, но -- раскручиваться! Поскольку момент этой силы ускоряет вращение. Если вперед (рис. 4 справа), то вращение будет тормозиться, но скорость центра тяжести будет расти! И то, и то -- очевидная глупость. Так как устроены силы, которыми поверхность действует на шарик?
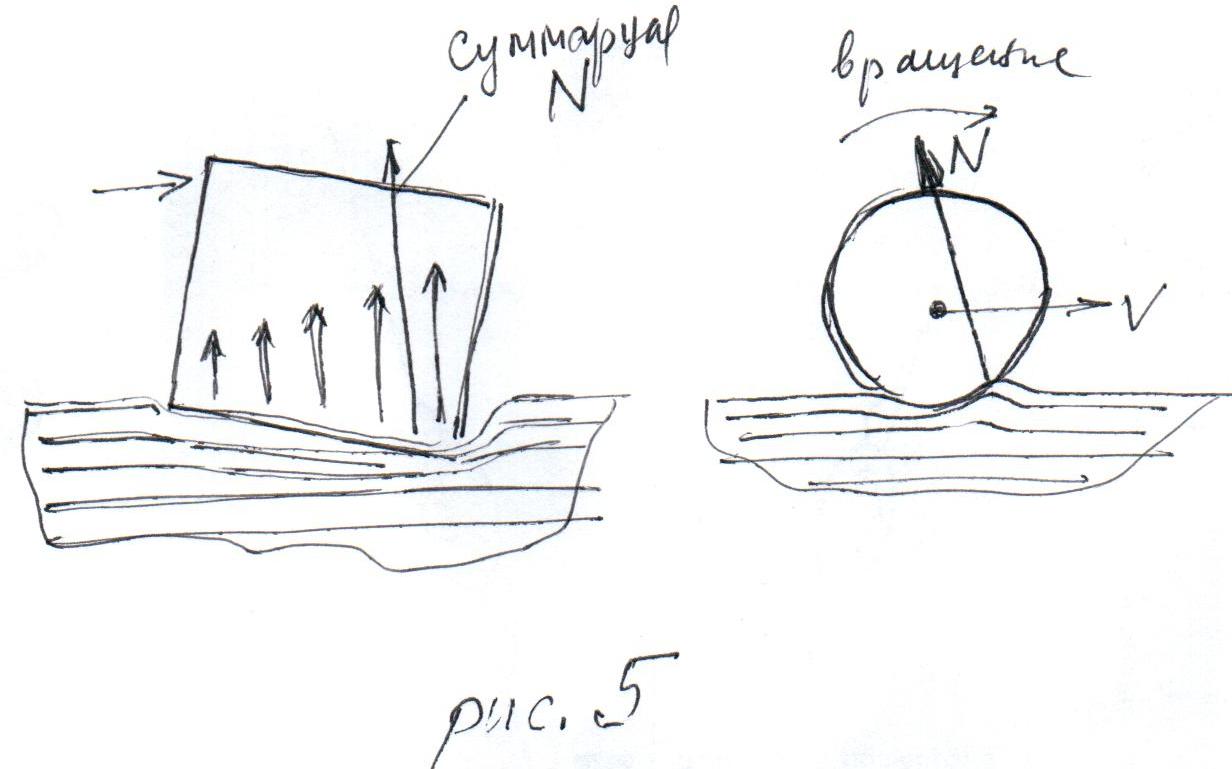
Что мы знает про суммарную силу, с которой поверхность действует на шарик? Ее вертикальная компонента должна быть равна mg, горизонтальная -- направлена назад по ходу, а ее момент должен тормозить вращение. Мы вынуждены нарисовать эту силу так, как показано на рис. 5 справа и сделать вывод, что для торможения катящегося шарика плоскость должна быть деформируема. На бесконечно жесткой плоскости бесконечно жесткий шарик будет катиться вечно. Ну, то есть до сжатия Вселенной, если оно когда-то произойдет... Впрочем, можно показать, что на бесконечно жесткой плоскости будет тормозиться не бесконечно жесткий шарик. Рисунок для этой ситуации сделайте сами.



