![]()
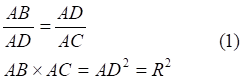
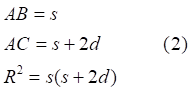
![]()
![]()
![]()
![]()
![]()
16.10 - 05.11.2021
2005, том 11, N 1, с. 227--239. No 2005, Центр новых информационных технологий МГУ, Издательский дом "Открытые системы"
|
| |
|
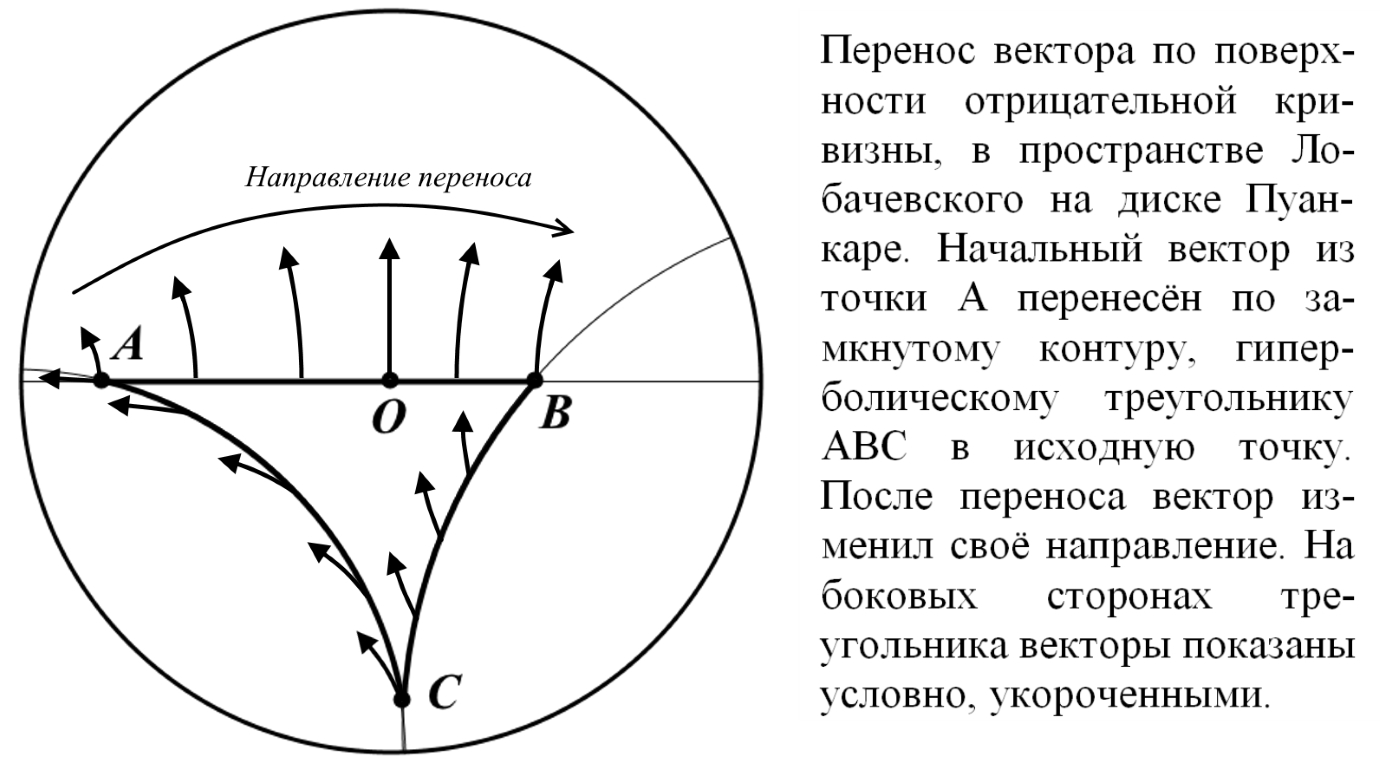
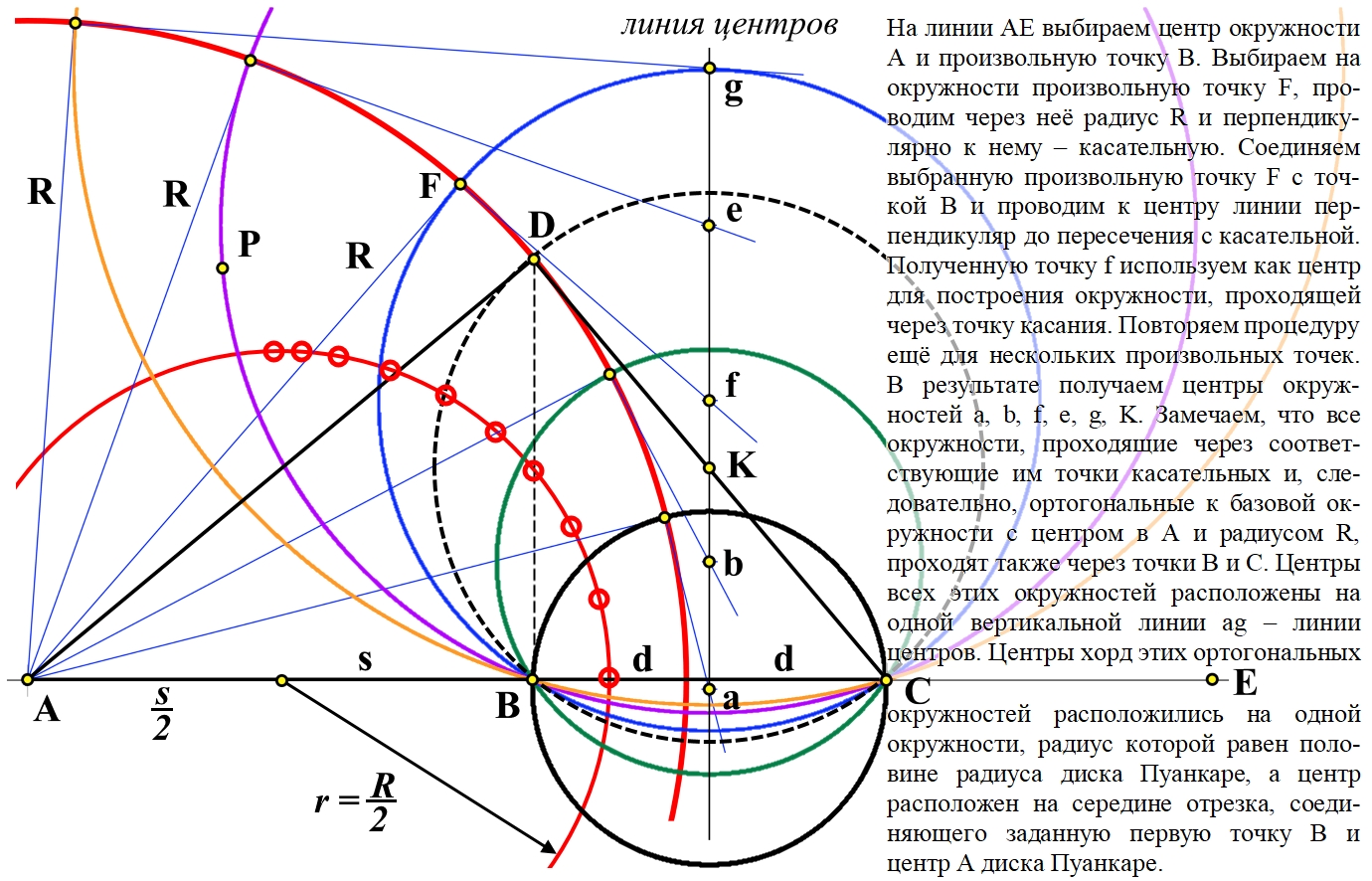
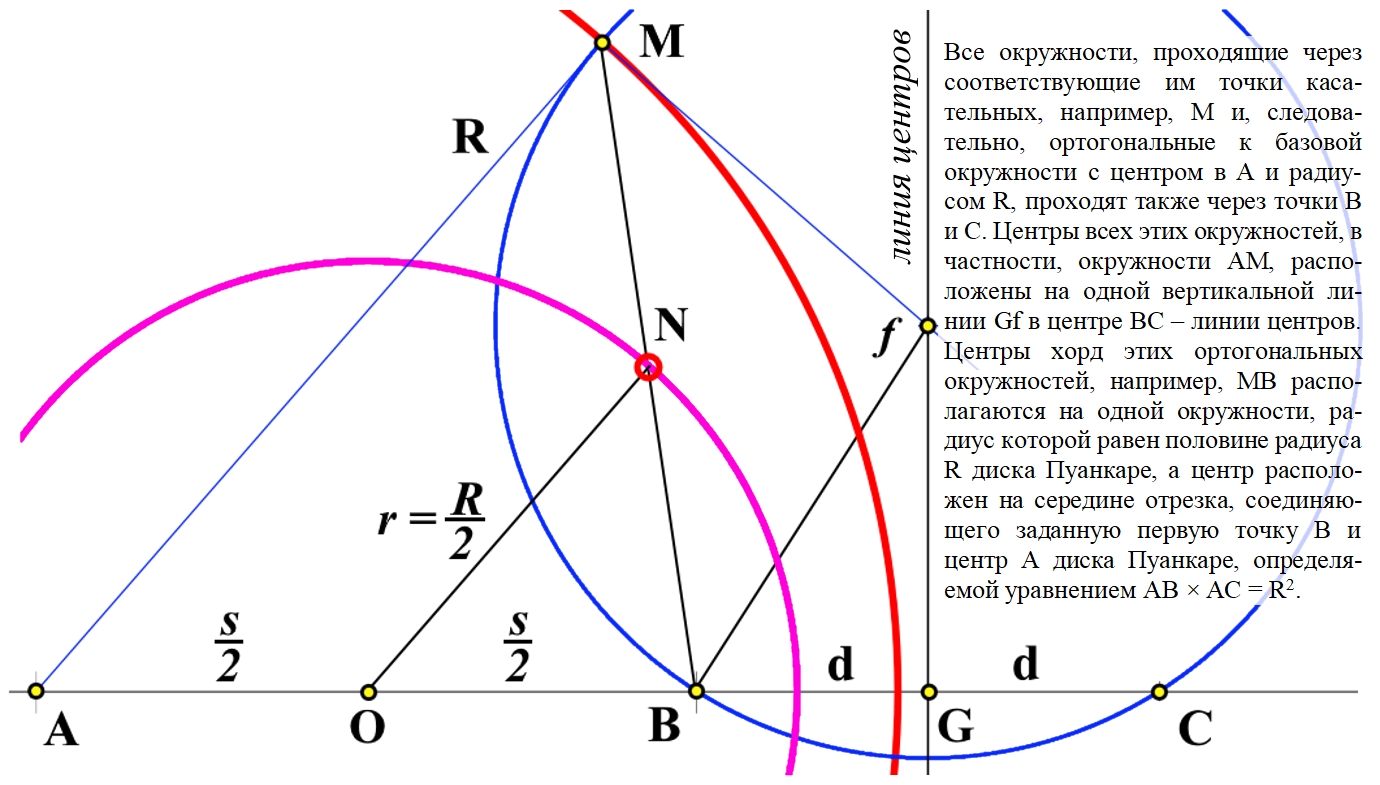
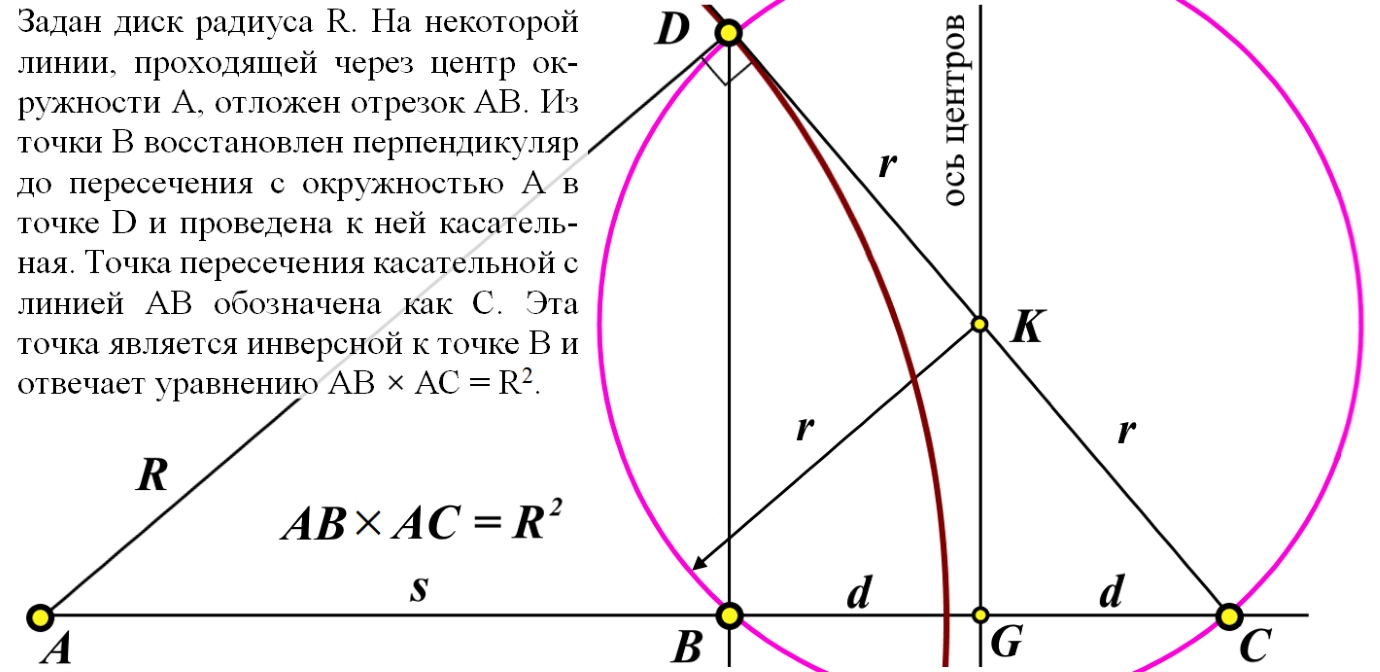
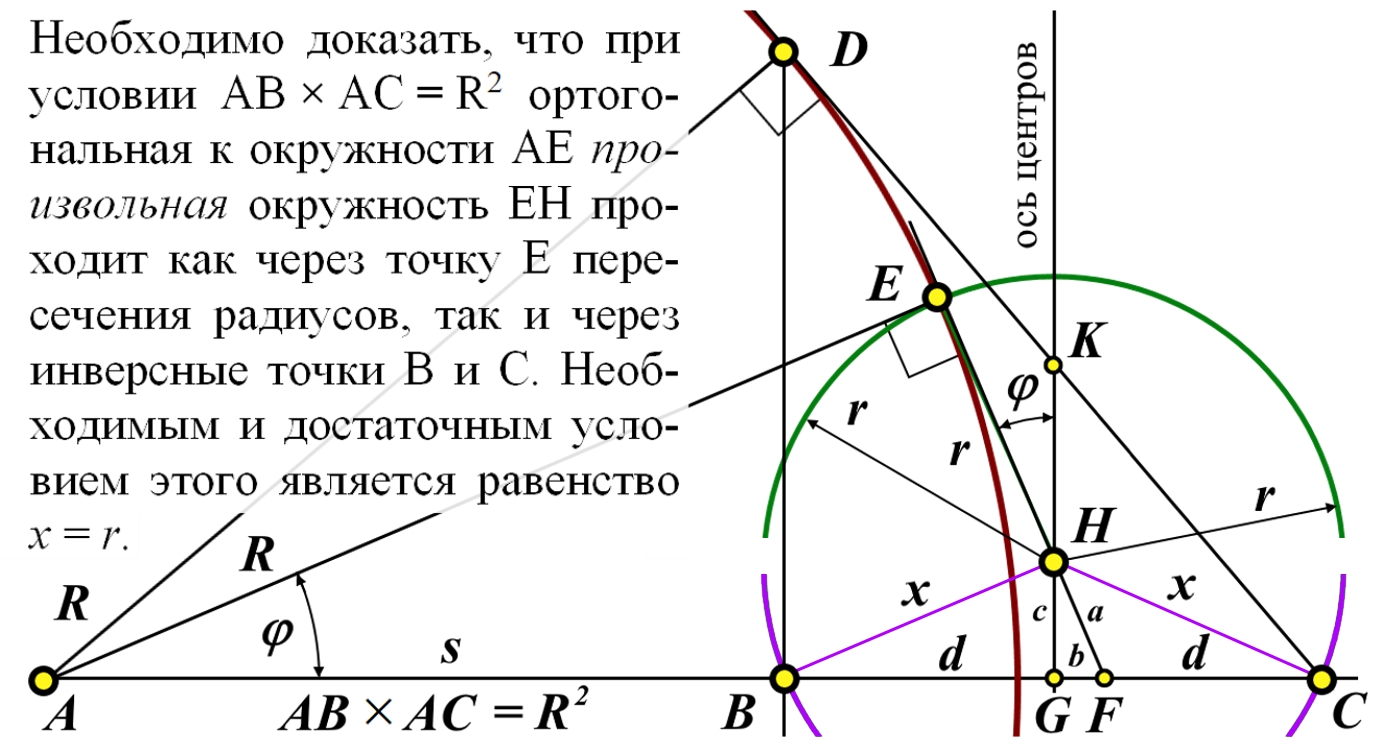
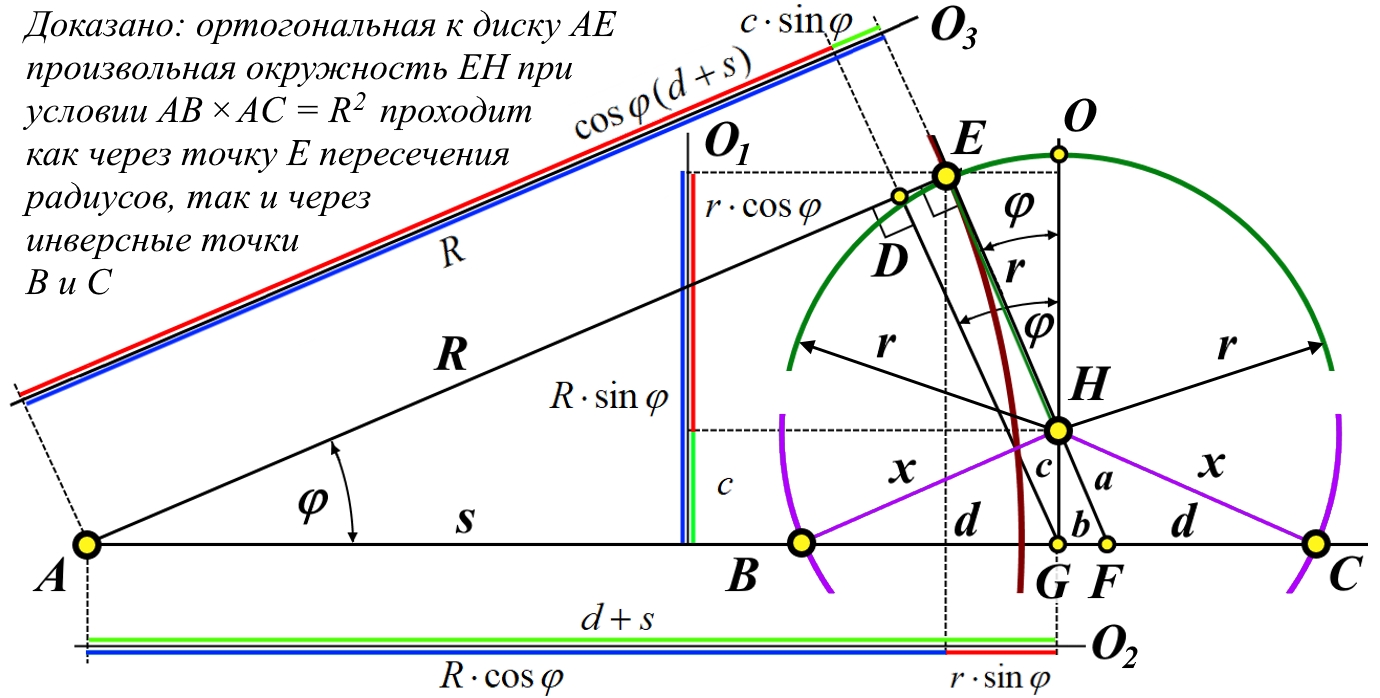
Демонстрационные иллюстрации параллельного переноса вектора на поверхностях отрицательной кривизны Лобачевского в общедоступной литературе отсутствуют. Такая иллюстрация на примере диска Пуанкаре приведена в данной работе. Подчёркнуто, что параллельный перенос в искривлённом пространстве невозможен в принципе, возможен только эквиугловой перенос - с сохранением угла вектора относительно траектории переноса. Описан способ построения на таком диске геодезических, проходящих через две произвольные точки. Приведено доказательство корректности такого построения, доказательство того, что все окружности, проходящие через инверсные точки пересекают абсолют диска ортогонально. В общедоступной литературе такое доказательство не найдено. There are no demonstration illustrations of the parallel transfer of a vector on surfaces of negative curvature of Lobachevsky in the public literature. Such an illustration using the Poincaré disk as an example is given in this work. It is emphasized that parallel transfer in curved space is impossible in principle, only equi-angle transfer is possible - while maintaining the angle of the vector relative to the transfer trajectory. A method for constructing on such a disk geodesics passing through two arbitrary points is described. A proof of the correctness of such a metode is given, a proof that all circles passing through "inverse points" intersect the absolute of the disk orthogonally. In the publicly available literature such proof has been foundlos. | |


![]()

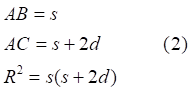



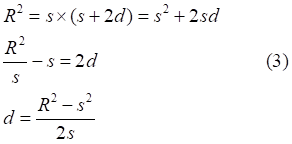
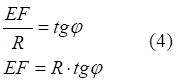
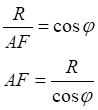
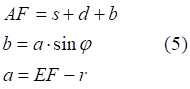
![]()
![]()
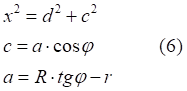
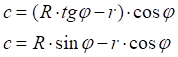
![]()
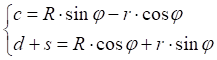
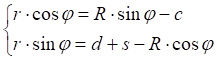
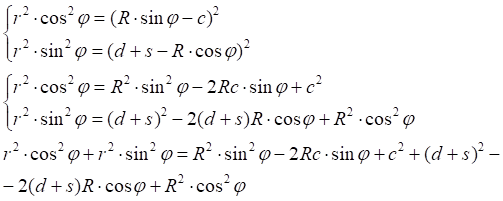
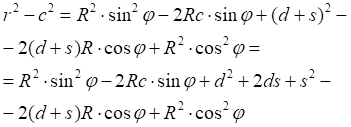
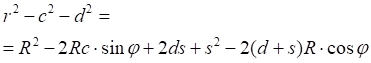
![]()
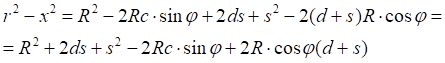
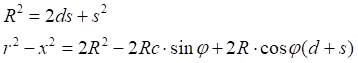
![]()
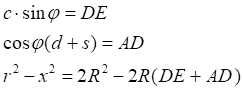
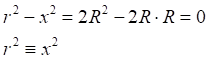
16.10 - 05.11.2021
|
|