Lib.ru : Федюкин Вениамин Константинович. Теория сверхдианамагничиваемости взамен ошибочной теории сверхэлектропроводимости тел

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

"Санкт-Петербургский государственный инженерно-экономический университет"

В. К. Федюкин

ТЕОРИЯ СВЕРХДИАНАМАГНИЧИВАЕМОСТИ

ВЗАМЕН ОШИБОЧНОЙ

ТЕОРИИ СВЕРХЭЛЕКТРОПРОВОДИМОСТИ ТЕЛ

0x08 graphic

Санкт-Петербург

2013

УДК 338.945:530.1

ББК 31.232я73

Ф32

Рецензенты:

- д-р эконом. наук, проф. В.П. Семенов - зав. кафедрой управления качеством и машиноведения СПбГИЭУ

- д-р физ.-мат. наук, проф. С.А. Атрошенко - ведущий научный сотрудник СПб. института проблем машиноведения РАН

- канд. физ-мат. наук, проф. СПб. гос. политехн. ун-та Д.П. Иванов

- канд. техн. наук, доцент СПбГИЭУ Л.В. Виноградов

Федюкин В. К.

Теория сверхдианамагничиваемости взамен ошибочной теории сверхэлектропроводимости тел. Монография. В. К. Федюкин. - СПб.: СПбГИЭУ, 2013. - 400 с.

В данной монографии изложена новая альтернативная, то есть не корпускулярная, не электронная, а магнитостатическая теория физического явления, ошибочно называемого сверхпроводимостью электрического тока. Доказывается противоречивость и неадекватность существующих теорий сверхпроводимости электричества при низких закритических температурах. Анализ соответствующих экспериментов показал, что в них проявляется не сверхпроводимость электрического тока, а метастабильная сверхдианамагничиваемость веществ в условиях низких температур. Представлены основы макро- и микроскопической теории сверхдиамагнетизма и изложены подходы к возможному использованию низко-, средне-, а также будущих комнатнотемпературных и действительно высокотемпературных сверхдиамагнетиков.

Предназначено научным работникам, инженерам, аспирантам, магистрам и студентам физических и технических специальностей, а также всем интересующимся проблемами физики и техники.

УДК 338.945:530.1

ББК 31.232я73

No В.К. Федюкин

2013

Предисловие

Настоящее издание является по существу усовершенствованным, исправным и дополненным вариантом монографии автора "Решение проблемы "сверхпроводимости" электрического тока и сверхдиамагнетизма" опубликованной в 2011 году. Та публикация посвящалась 100 - летнему юбилею провозглашения голландским исследователем Гейке Камерлинг-Оннесом открытия сверхпроводимости электрического тока металлами при глубоко низких температурах. За истекшее время интерес читателей к изложенной в монографии теории возрос, что, очевидно, обусловлено актуальностью решения проблемы сверхпроводимости. Кроме того, вышеназванная монография с решением застарелой проблемы сверхпроводимости была напечатана внутри вузовском издании Санкт-Петербургского инженерно-экономического университета пробным тиражом всего 100 экземпляров. Востребованность читателей в этой книге не была удовлетворена. Интерес к работе автора над теорией явления, обнаруженного в лаборатории Оннеса, возрос в связи с публикацией (тоже 100 экземпляров) брошюры "Миф о сверхпроводимости электричества как следствие научной фальсификации", 2012 г. Более ранние публикации автора на тему о "сверхпроводимости" и сверхдиамагнетизме тоже способствовали тому, чтобы написать данную обновленную монографию.

Содержание, предлагаемой научной общественности, монографии кратко можно сформулировать как опровержение теории несуществующей "сверхпроводимости" и разработка альтернативной теории явления, обнаруженного впервые работниками научно-экспериментальной лаборатории, руководимой Камерлинг-Оннесом, как эффекта (свойства) более сильного, то есть сверхдианамагничивания тел при крайне низких температурах.

Считается, что существует чудесное явление, суть которого состоит в способности различных материалов проводить электрической ток абсолютно без сопротивления в условиях криогенных температур. Поэтому, утверждают некоторые ученые, такой необычный электрический ток "сверхпроводимости" может и якобы течет, например, в кольцеобразном образце неограниченно (бесконечно) долго. Однако общеизвестно, что не бывает движений без сопротивлений и что в природе "всякому действию есть противодействие". Это общий закон механики Ньютона и основные законы термодинамики, а также материалистическая философия, не допускают сверхестественного, в частности, "сверхпроводимости" электрического тока и движения электронов без какого-либо сопротивления со стороны проводника. Следовательно, идея и теории "сверхпроводимости" электричества, противоречат основам науки и поэтому они антинаучны. Устранение этих противоречий было и есть главной задачей теоретического исследования, изложенного в данной книге.

В настоящее время необходимость решения проблемы "сверхпроводимости" стала особенно актуальной. Передовые государства тратят огромные средства для практического использования "сверхпроводимости". Примером, этого является создание сверхпроводникового ускорителя элементарных частиц материи, то есть большого адронного коллайдера (БАК). Существует много других, как правило, безуспешных, проектов использования именно "сверхпроводимости" электрического тока, а не низкотемпературного сверхдиамагнетизма. Фантастические замыслы использования "сверхпроводимости" электричества не оправдали надежд. Все это требует пересмотра исходных представлений и теорий "сверхпроводимости".

В результате анализа экспериментальных данных и их интерпретаций, а также теорий "сверхпроводимости", создается убеждение, что "сверхпроводимости" электрического тока, в современном его понимании, не существует и не может существовать, а есть метастабильное сверхдианамагничивание веществ при низких и очень низких температурах. Это новое понимание рассматриваемого явления (свойства веществ) привело к созданию основ и элементов, составляющих теорию сверхдиамагнетизма.

Представляется очевидным, что решение вековой научной проблемы "сверхпроводимости" электричества состоит в отрицании этой проблемы, так как не существует самой "сверхпроводимости" электричества. Доказывается, что существует не "сверхпроводимость", а реально измеряемое явление сверхдианамагничиваемости и диэлектризации веществ в условиях низких температур меньших определенной критической температуры.

Вероятно, что изложенная здесь концепция и соответствующая теория вызовут дискуссию, появятся оппоненты с возражениями, замечаниями, критикой или одобрениями, что, безусловно, будет способствовать постижению (установлению) истины и, следовательно, научному прогрессу в области физики и практических наук, а такие более широкому практическому использованию сверхдиамагнетизма.

Обращаясь к читателям этой книги, автор надеется, что его позиция и аргументация будут восприняты не предвзято, не огульно отрицательно, как это бывает, а заинтересованно, аналитически и с признанием допустимости иного, нетрадиционного понимания явления, называемого сейчас "сверхпроводимость".

Аргументированная критика, доказательные возражения и замечания, а также предложения и пожелания будут приняты автором с благодарностью.

Автор выражает большую благодарность студенткам Санкт-Петербургского государственного инженерно-экономического университета Константину Ефимову и Роману Иванову за компьютерное оформление рукописи этой книги.

ВВЕДЕНИЕ

Известно, что наука как результат познавательной деятельности людей не защищена от ошибок. История науки знает много случаев ошибочного толкования и теорий сущности отдельных явлений и предметов. К числу таких противоречивых, непонятных и необъяснимых явлений относится так называемая "сверхпроводимость" электрического тока различными материалами при очень низких температурах. При этом утверждается, что электрический ток течет абсолютно без сопротивления со стороны проводника. Это неочевидное и невероятное суждение укоренилось в науке и давно занимает умы не только физиков, но и многих других ученых, инженеров, предпринимателей, а также людей, интересующихся наукой. Всем хочется узнать и понять как это, вопреки всеобщему закону о том, что "всякому действию есть противодействие", что "любому движению есть сопротивление среды, в которой движется объект", всё же есть исключительное явление, когда, например, в металлическом проводнике электроны (переносчики энергии) перемещаются без какого-либо противодействия со стороны атомов токопроводящего вещества.

Конечно же, очень заманчиво иметь проводники электричества без сопротивления и создавать на этой основе супертехнику будущего. Желательно, используя "незатухающие электрические токи в сверхпроводниках", создать пресловутый "вечный двигатель" и т.д. Однако подобным мечтам людей, по-видимому, не суждено осуществиться, так как исследования в указанных направлениях ведутся давно, но пока безуспешно. Нет удовлетворительной научной теории "сверхпроводимости" и поэтому нет давно ожидаемых практических результатов ее применения. Имеющиеся результаты в этой области относятся к экспериментальным, но они не обязательно обусловлены "сверхпроводимостью".

Прошло уже более 100 лет с тех пор, как было обнаружено феноменальное физическое явление, необоснованно названное Хейке Камерлинг-Оннесом сверхпроводимостью. Однако до сих пор физическая природа этого явления остается загадочной и непонятной. Многократные попытки создать достоверную микроскопическую теорию "сверхпроводимости" оказались неудачными, а предлагавшиеся феноменологические описания этого явления противоречивыми и "не освещающими путь практике".

Учеными разных стран выполнены многочисленные теоретические исследования, а проблема научного объяснения невероятной "сверхпроводимости" электрического тока металлами и другими материалами остается нерешенной. Ведутся нескончаемые дискуссии о физической природе "сверхпроводимости". Но, очевидно, без четкого понимания того, что такое "сверхпроводимость", без модели и без приемлемой микроскопической теории этого явления как оснований для создания общей физической теории, решение проблемы получения указанного эффекта при естественных температурах сильно осложнено и вряд ли может быть осуществлено в ближайшие годы. А вот колоссальный энергомагнитный эффект, ошибочно, по нашему мнению, названный "сверхпроводимостью", может получить широкое применение в производственной и потребительской практиках.

После первых публикаций Камерлинг-Оннеса по вопросам так называемой "сверхпроводимости" была надежда, что будет создана подходящая микроскопическая теория "сверхпроводимости". Однако этой надежде не суждено было осуществиться. Причиной отсутствия пригодной теории "сверхпроводимости", по-видимому, является консерватизм мышления. Ученые прежних лет не пытались отойти от привычного представления об электрическом токе, об электронном строении атомов и проводников. Для решения таких запутанных и сложных, почти тупиковых проблем, как теория "сверхпроводимости", необходимы нетрадиционный подход, принципиально иные идеи, другая парадигма. Необходимо представить научной общественности иное видение (понимание) того, что на самом деле открыл Камерлинг-Оннес в 1911 г.

Здесь и в предшествующих публикациях автора доказывается, что явление, обнаруженное Камерлинг-Оннесом, не есть "сверхпроводимость" электричества с нулевым сопротивлением движению электронов и их энергии по проводнику. Следовательно, все существующие теории "сверхпроводимости" (микро- и макроскопическая, а также квантово-механическая и другие феноменологические теории) не имеют к этому явлению отношения и поэтому в принципе не могут быть правильными. Они все являются ошибочными, антинаучными, так как объясняют то, чего объективно нет в природе, а не то, что есть на самом деле.

Научный анализ "проблемы сверхпроводимости" показывает, что "сверхпроводимость", в ее современном понимании, в природе не существует, а обнаружено было исследователями другое физическое явление - более сильное чем обычно, дианамагничивание веществ при низких температурах, что не одно и то же. Установление истины и решение проблемы нереальной "сверхпроводимости" необходимо осуществить как можно быстрее. Очевидно, что начинать эту работу надо с рассмотрения источника, аргументов и логики возникновения идеи об абсолютной "сверхпроводимости". Поэтому в данной работе вначале выполнен анализ первых публикаций об открытии так называемой "сверхпроводимости" электрического тока без сопротивления.

Здесь автор обосновывает тот факт, что объективно мы имеем дело не с эффектом "сверхпроводимости", а с переходом материалов в сверхмагнитное, точнее, в сверхдиамагнитное состояние при температурах ниже критической. Такое понимание явления, открытого Камерлинг-Оннесом, поможет решить многие проблемные вопросы рассматриваемого перехода материалов в состояние сверхдиамагнетизма. Понятия о сверхмагнитном и, в частности, о, сверхдиамагнитном состоянии веществ означают то, что в условиях закритически низких температур, материальные объекты (тела) дианамагничиваются на много больше (сильнее), чем при более высоких температурах. Критическая температура (Т_кр) перехода тел к способности сверхдианамагничиваться есть особенная низкотемпературная, но все же одна из, так называемых, магнитных точек Кюри.

Автор намерен продолжать работу по созданию адекватной теории сверхдиамагнетизма веществ. Неоценимой помощью в этом деле будут замечания и рекомендации тех, кто вступит с автором в доброжелательную научную дискуссию.

1. НЕРЕШАЕМАЯ ПРОБЛЕМА "СВЕРХПРОВОДИМОСТИ" ЭЛЕКТРИЧЕСКОГО ТОКА

Считается, что существует сверхпроводимость электрического тока как процесс передачи различными материалами электрической энергии посредством движения в них электронов без какого-либо сопротивления этому движению со стороны проводника. Данное нереалистическое представление о сверхпроводимости тока как о почти сверхъестественном явлении природы вот уже скоро 100 лет занимает умы ученых, инженеров и других специалистов. Потрачены колоссальные интеллектуальные и финансовые усилия, а проблема адекватного понимания и создания соответствующей теории, а также широкого использования сверхпроводимости остается нерешенной. Известно, что по проблеме сверхпроводимости опубликованы десятки тысяч работ. В настоящее время по вопросам сверхпроводимости ежедневно публикуется по 10-15 статей, издаются большие монографии, проводятся многочисленные симпозиумы и конференции. За исследования сверхпроводимости присвоено несколько Нобелевских премий и ряд национальных премий. Такой повышенный научный и общественный интерес к необычной сверхпроводимости обусловлен очевидной невероятностью объяснений ее физической природы и чрезмерно большими ожиданиями от использования этого физического явления. Однако вековая задержка в создании приемлемой теории сверхпроводимости свидетельствует о том, что вероятно в исходных основах (представлениях и интерпретациях экспериментов) для теоретических и практических исследований есть принципиальные ошибки. Возможно, поэтому до сих пор нет ясности в понимании физической природы данного явления и нет непротиворечивой теории сверхпроводимости. Все это вызывает необходимость разобраться в сущности явления (необоснованно называемого сверхпроводимостью электрического тока) начиная с момента его экспериментального обнаружения в Лейденской лаборатории (г. Лейден, Голландия) Хейке Камерлинг-Оннесом с сотрудниками еще в 1910-1911 г.

Приступая к анализу проблемы сверхпроводимости необходимо определиться в отношении правильности используемых терминов и их понятий.

Исходя из наиболее упрощенного и поэтому не адекватного представления об электрическом токе как о направленном движении в телах каких-то, как-то и чем-то заряженных частиц, в частности, электронов или ионов, получаем сугубо предположительное: "Электрический ток - это движение заряженных частиц". Но ведь электрический ток мы оцениваем по измерениям уменьшения "электротонического состояния" (М. Фарадей [103]), то есть по величине к изменению электрического потенциала (напряжения) электрического поля у поверхности проводника, иначе говоря, по уменьшению величины потенциальной (запасенной) энергии электрического поля при преобразовании ее в другие виды энергии. Движений, например, электронов внутри проводника пока еще никто не наблюдал. Следовательно, объективно и достоверно можно утверждать только то, что электрический ток есть передача электромагнитным полем электрической энергии от ее источника к потребителю (преобразователю). Очевидно, что носителем энергии электрического тока проводимости является движущаяся определенным образом полевая материя (эфир).

Вне сомнений, что "всякому действию есть противодействие" и, следовательно, "всякому движению есть сопротивление" (И. Ньютон). Естественно, что и электрический ток передается по проводнику с соответствующим сопротивлением (закон Ома). Общепринято сейчас, что "электрическое сопротивление это величина, характеризующая противодействие, которое оказывает проводник движущимся в нем электрическим зарядам (в частности, электронам)". Но возможно и другое определение электросопротивления. Например, сопротивление электрическому току это есть самоиндукционное (самовозникающее) электромагнитное противодействие движению электромагнитной энергии со стороны любых материальных объектов. В данном определении нет предполагаемых относительно медленно движущихся "свободных" электронов и их рассеяния атомами вещества. Это устраняет ряд принципиальных противоречий в теории электричества. Например, электрический ток проводимости не может переноситься ни электронами, ни ионами, так как их скорости движения внутри тел малы, а скорость распространения электрического тока по проводнику примерно равна скорости света, то есть 300000 км/с. Из этого факта следует, что электрический ток есть движение электромагнитного поля внутри и вблизи проводника. Но вопреки фактам и логике электрическим током проводимости по-прежнему называют такой поток электрической энергии, когда ее носители, то есть микроскопические электрические заряды, движутся внутри макроскопического тела (твердого, жидкого или газообразного).

Однако существуют основания утверждать, что электрический ток проводимости не есть движение свободных электронов в некоторых твердых и жидких телах, а является процессом передачи электрической энергии посредством ламинарных (струйных) или турбулентных (колебательных, спиралеобразных, вихревых) электромагнитных движений бесструктурной невещественной материи (по-старому, эфира) вдоль поляризованных атомных или молекулярных структур токопроводящего вещества и что сверхпроводимости электричества сверхтекучими спаренными электронами не существует. Поэтому в дальнейшем слово "сверхпроводимость" используется автором в кавычках.

Давно известно, что электрическое сопротивление большинства металлов и многих других токопроводящих тел уменьшается с понижением их температуры и при очень низких температурах стремится к некоторому минимальному пределу - остаточному электросопротивлению. Это остаточное электросопротивление, например, чистых металлов, при температурах в пределах - 192-258®С во много раз меньше, чем при комнатных и повышенных температурах (см. рис. 5). Такое снижение электросопротивления до очень малых значений на практике часто принимают за сверхпроводимость электричества. Постепенное и большое уменьшение сопротивления электрическому току в результате глубокого охлаждения проводника не является переходом его в сверхпроводящее состояние. Такой процесс не соответствует установившемуся в науке понятию о скачкообразном переходе переохлажденного материала к "сверхпроводимости" электрического тока абсолютно без сопротивления со стороны токопроводящего материала. Кроме того, известно, что у многих простых веществ и сложных материалов есть обратная зависимость электросопротивления от температуры проводника. Однако уменьшение электросопротивления при увеличении температуры материала не приводит к его "сверхпроводимости". Типичным представителем вещества с отрицательным (уменьшающим) температурным коэффициентом сопротивления (ТКС) при увеличении температуры является кремний. Его удельное электросопротивление уменьшается с 2,97 Ом?мм²/м при при температуре -192®С до 0,23 Ом?мм²/м при +800®С (100 мкОм?см=1 Ом?мм²/м). Температурный коэффициент сопротивления характеризует уменьшение удельного электросопротивления ? при изменении температуры на 1®С или на 1К.

Изменения отрицательного ТКС кремния в широком диапазоне температур, при измерении ? в мкОм?см, таковы:

- ТКС_ср=1,3 мкОм?см/®С при температурах от -192®С до -78®С,

- ТКС_ср=0,7 мкОм?см/®С при температурах от -78®С до 0®С;

- ТКС_ср=0,2 мкОм?см/®С при температурах от 0®С до 100®С,

- ТКС_ср=0,2 мкОм?см/®С при температурах от 100®С до 200®С.

При дальнейшем нагревании ? кремния несколько увеличивается, а потом вновь снижается.

Отрицательный ТКС имеют такие материалы как графит, полупроводники (например, легированные германий и кремний), стеклообразные полупроводники, соединения и смеси поликристаллических окислов металлов (MnO, CoO, NiO, CuO, Fe₃O₄, UO₂ и др.). Еще М. Фарадей обнаружил отрицательный ТКС у сернистого серебра и фторида свинца. Отрицательным ТКС обладают материалы сложных систем, таких как NiO-Ca₂O₃-Mn₂O₃или NiO-Mn₂O₃ и др.

Примером вещества с положительным ТКС является висмут. Значения его ТКС при различных температурах таковы:

-- ТКС_ср=0,22 мкОм?см/®С при температурах от -258®С до -192®С,

-- ТКС_ср=0,35 мкОм?см/®С при температурах от -192®С до -78®С,

-- ТКС_ср=0,41 мкОм?см/®С при температурах от -78®С до 0®С,

-- ТКС_ср=0,49 мкОм?см/®С при температурах от 0®С до 100®С,

-- ТКС_ср=0,69 мкОм?см/®С при температурах от 100®С до 200®С.

При этом удельное электросопротивление висмута при 20®С равно 114,05 мкОм?см или 1,14 Ом?мм²/м.

В связи с вышеизложенным, отметим, что в "сверхпроводящее" состояние переходят все материалы как с положительными, так и с отрицательными ТКС. Но материалы с положительными ТКС переходят в "сверхпроводящее" состояние при очень низких температурах (от 0 до 30К). Это низкотемпературные "сверхпроводники" 1-го рода. Материалы с отрицательными значениями ТКС - это относительно высокотемпературные "сверхпроводники" 2-го рода. В среднем критическая температура перехода в "сверхпроводящее" состояние (Т_кр) у "сверхпроводников" 2-го рода в 5-6 раз больше, чем у "сверхпроводников" 1-го рода. Этот примечательный и не случайный факт с очевидностью свидетельствует о том, что при отрицательном ТКС материалу легче и быстрее перейти из токопроводящего к диэлектрическому и диамагнитному состоянию. Следовательно, можно предположить, что при создании комнатнотемпературных и теплых (с Т_кр>100®С) "сверхпроводников", а по-существу диэлектрических сверхдиамагнетиков, необходимо подбирать вещества, их соединения и композиции (система) с наибольшими удельными электросопротивлениями и с максимальными значениями отрицательных ТКС. Поэтому не случайно многочисленные эксперименты показывают, что хорошие проводники являются плохими "сверхпроводниками", а непроводники, то есть диэлектрики, в частности, керамические материалы - изоляторы, при более высоких температурах становятся хорошими "сверхпроводниками". Почему так происходит? Ответ на этот вопрос, очевидно, состоит в том, что рассматриваемое явление "сверхпроводимости" не является таковым, Это нечто другое. В частности, это есть сугубо магнитное проявление вследствие изменения электронной структуры атомов. Доказательства данного суждения приводятся ниже и изложены в ранее опубликованных работах автора по проблеме "сверхпроводимости" [106-110].

Рассмотрим кратко, как было обнаружено и исследуется то, что называется сверхпроводимостью электрического тока. Голландский ученый Хейке Камерлинг-Оннес (кратко Оннес) в 1911 г. производил опыты по определению электросопротивлений металлов при температуре жидкого гелия 4,2К. Эксперименты Оннеса и его последователей производились двояко: 1. пропусканием постоянного электрического тока по исследуемому проводнику и 2. путем предполагаемой индукции какого-то электрического тока в кольцеобразном металлическом образце под действием постоянного ферромагнита.

В первом случае измерение электросопротивления производилось потенциометрическим способом - гальванометром (т. к. токи были малы), а во втором - электросопротивление оценивалось по показаниям магнитометра. Так это делают и сейчас. При гальванометрическом (потенциометрическом) способе измерения исследуемая металлическая проволока подключалась последовательно в цепь постоянного тока и определялась разность электрических потенциалов на её концах. По разности потенциалов (?Е) можно косвенно судить об электросопротивлении проводника электрическому току. При магнитометрическом измерении можно определить силу магнитного поля на некотором расстоянии от токопроводящей проволоки или иного проводника, но не его электросопротивление. Если электрического тока в проводнике нет, а магнитное поле вблизи него есть, то магнитометром измеряется намагниченность (M) исследуемой проволоки или другого твердого тела. Магнитометром, измеряющим внешнее магнитное поле около проводника с током, в принципе нельзя измерить ни электросопротивление (R), ни достоверно определить наличие тока в проводнике, т.к. постоянное магнитное поле вполне может быть у тела и без электрического тока в нем.

Исследования Оннеса показали, что при гелиевой температуре на концах токопроводящей платиновой проволоки разность потенциалов ?Е, измеряемая обычным гальванометром, внезапно исчезает. [31, 111]. Несколько ранее это же явление наблюдал сотрудник Оннеса по Лейденской криогенной лаборатории квалифицированный физик Гиллес Холст [31]. Это удивительное явление слишком долго остается предметом научных дискуссий, потому что оно было необоснованно названо Оннесом сверхпроводимостью электрического тока, т. е. электрическим током без сопротивления или с "сопротивлением" R=0. До сих пор считается, что неограниченно большой электрический сверхток проскакивает по сверхпроводящей проволоке без сопротивления, т.е. как при коротком замыкании проводов в обычных условиях токопроводности. Но на практике короткого замыкания от наступления "сверхпроводимости" не происходит. Это означает, что отсутствие падения напряжения (?Е=0) не от "сверхпроводимости" первого рода с R=0, а от чего-то другого.

Из факта исчезновения разности потенциалов (напряжений) ?Е непосредственно на концах платиновой и других токопроводящих проволок, находящихся под электронапряжением от источника постоянного (не знакопеременного) напряжения (например, от электрической батареи, как в опытах Оннеса и других), можно сделать вывод о том, что металлические проволоки при гелиевых температурах становятся не сверхпроводниками, а наоборот, диэлектриками, т.е. изоляторами с R=? для данного токопроводящего материала при определенных для него докритических значений электрического E и магнитного H полей. Следовательно, при наступлении так называемой "сверхпроводимости" первого ряда любых материалов (в том числе и металлических) электрический ток не течет и поэтому ?Е=0. При ?Е=0, когда нет тока, а электрическая напряженность внешнего поля Е есть и воздействует на "сверхпроводник", то логичнее утверждать что электросопротивление R=?, а не R=0. Электросопротивление равно нулю возможно только в случае, когда нет электрического тока в проводнике.

Кстати отметим, что еще в 1936 г. Я. И. Френкель указывал "что в отношении своей теплоемкости тело в сверхпроводящем состоянии ведет себя как диэлектрик, т.е. так, как если бы в нем вовсе не было свободных электронов" [111.С.15].

Причина прекращения тока проводимости в металлах, и других токопроводящих материалах, то есть прекращение потока энергии электромагнитного поля по проводнику, при температуре ниже критической, состоит, по-видимому, в появлении у этих материалов сильного, блокирующего ток, противополя - сверхдиамагнитного поля, которое, как известно, при последующем увеличении E или H разрушается, и ток проводимости восстанавливается с прежним электросопротивлением. Эти утверждения автора подтверждаются результатами многих экспериментов по изучению "сверхпроводимости". Так, например, Оннес и его последователи экспериментировали с кольцеобразными проводниками, не пропуская по ним электрический ток от внешнего источника. Они ошибочно полагали, что при гелиевой температуре под действием постоянного магнитного поля в металлическом кольце индуцируется постоянный сверхпроводимый электрический ток, который, по их мнению, не затухая, может циркулировать в кольце неограниченное время, а это означает, что R=0. Отметим, кстати, что еще Фарадей в середине 19-го века доказал, что постоянное магнитное поле не может индуцировать электрический ток. Оно способно только намагничивать тела. Однако результаты Оннеса и других до сих пор неверно интерпретируются как сверхпроводимость.

В процессе кратковременного воздействия постоянным магнитом на кольцеобразный металлический образец, находящийся в дюаре при температуре жидкого гелия, он становился диамагнитным и его более сильную намагниченность измеряли за пределами дюара магнитометром. Наведенное сверхмагнитное поле кольца сохраняется стабильным (при закритической криогенной температуре) неограниченное время. Но из этого не следует, что в кольце циркулирует особенный и более сильный электрический ток без сопротивления со стороны проводника и что закон Ома и многие другие законы в данных условиях экспериментов не действуют. В опытах с кольцами проявляются законы магнетизма, а не электрического тока. Наличие постоянного магнитного поля вблизи кольца доказывает его намагниченность, а не то, что в нем будто бы течет неестественный сверхток сверхпроводимости.

Оннес, экспериментируя, разрезал обычное немагнитное свинцовое кольцо, в котором, как предполагалось, индуцирован сверхпроходящий электрический ток и ожидал исчезновения тока и исчезновения вблизи кольца магнитного поля. Однако, отклонение магнитной стрелки, регистрирующей силу магнитного поля, при разрезании кольца не изменялось, "как если бы кольцо представляло собой ... магнит" [111. С. 5]. Этот эффект, обнаруженный впервые Оннесом, и все аналогичные эффекты так называемых "контактов Джозефсона" легко объясняются магнитными взаимодействиями, аналогично тому, как это происходит между сближеными частями некогда единого постоянного магнита или между пластинами обычного конденсатора. Следовательно, все известные контакты Джозефсона это не электрические контакты сверхпроходящих по ним токов, а усиленные и высокочувствительные контакты более магнитовосприимчивых тел. Эксперименты подтверждают, что в этих контактах нет энергозатратных туннельных эффектов прохождения электронов через нетокопроводящие барьеры, а есть практически энергонезатратные магнитные взаимодействия тел через зазоры или диэлектрические материалы между ними. Такое, только на первый взгляд, необычное магнитное контактирование происходит потому, что материалы контактов при закритических криогенных температурах переходят в состояние сильной намагничиваемости с большим дальнодействием их полей.

Установлено, что существует только два статических способа перевода материала в "сверхпроводящее" состояние: электростатический, то есть посредством пропускания постоянного электрического тока по проводнику и магнитостатический - под влиянием постоянного магнитного поля.

При электростатическом способе металлическая проволока включается в электрическую сеть постоянного электрического тока. Та часть проволоки, которая охлаждается до температуры меньше Т_кр, становится как бы "сверхпроводящей". При этом разность электрических потенциалов на концах "сверхпроводящего" участка проволоки неожиданно становится нулевой. Их этого факта почему-то делается вывод не о том, что ток прекращается, а что электросопротивление становится нулевым. Более того, утверждается, что если отключить источник постоянного тока, а концы участка "сверхпроводящей" проволоки быстро соединить (замкнуть), то ток "сверхпроводимости" в таком замкнутом контуре течет бесконечно долго. Это утверждение полностью соответствует ошибочной гипотезе о возможном создании вечного двигателя. Ошибочным основанием для такого умозаключения, является то, что магнитное поле вблизи "сверхпроводящей" проволоки или контура неопределенно долго (бесконечно) остается неизменным. Однако повторим, наличие у "сверхпроводника" устойчивого и увеличенного магнитного поля не обязательно свидетельствует о существовании в нем "сверхтока" да еще и без сопротивления. Магнитное поле, как известно, может существовать и отдельно, независимо от электрического тока. Кроме того, отсутствие у "сверхпроводящего" материала электрического поля доказывает, что в нем нет тока (движения) электрически заряженных частиц. А что есть? Остается одно: есть самоиндуцированная сверхдианамагниченность материала. Эксперименты показали, что при переходе материалов в так называемое "сверхпроводящее" состояние у них появляется сильное и метастабильное именно диамагнитное поле, то есть сверхдиамагнитное поле.

В случае магнитостатики, когда на глубоко охлажденный (до Т<Т_кр) и не обязательно токопроводящий материал воздействуют постоянным магнитным полем от внешнего источника, будь то обычный ферромагнит или катушка соленоида с током, то в материале возникает тот же эффект не "сверхпроводимости", а сверхдианамагничиваемости. Отличие данного способа сверхдианамагничивания состоит в источнике индуцирующего магнитного поля. В первом способе источник индуцирующего магнитного поля внутри самого токопроводящего материала, а во втором, он вне его, то есть происходит индукция не тока, а диамагнитного поля от другого (внешнего) источника, что является магнитной взаимоиндукцией.

При исследовании сущности рассматриваемого природного явления необходимо различать магнитную индукцию изменяющегося (непостоянного, переменного) электрического тока и магнитную индукцию намагничивания. Магнитная индукция намагничивания (стабильное намагничивание или такое же размагничивание) происходит при продолжительном взаимодействии стационарных (постоянных) магнитных полей, а индукция электрического тока состоит в возникновении потока электрической энергии под влиянием потока переменных электромагнитных полей от внешнего источника.

Вот еще один аргумент доказательства сверхдиамагнитной сущности "сверхпроводимости". Известно, что ферромагнетики переходят в "сверхпроводящее", а по существу в диамагнитное, состояние при более низких температурах, чем другие материалы. Ферромагнетизм сильно противодействует появлению "сверхпроводимости", экспериментально обнаруживаемой как сверхдиамагнитное поле. Естественно, что ферромагнетизм затрудняет переход к сверхдианамагничиваемости ферромагнетиков. Ферромагнетизм обусловлен поляризацией атомных магнитных диполей, состоящих из двух электронов с определенными установившимися спинами. Увеличение энергии (скорости) движения внешних электронов по своим орбитам в атомах очевидно изменяет спины электронов на противоположные, что изменяет парамагнитную и ферромагнитную поляризацию атомов на диамагнитную. Понятно, что чем более сильный ферромагнетик с его легкой намагничиваемостью при обычных температурах, тем больше охлаждение требуется для перехода ферромагнетика в сверхдиамагнитное состояние, то тем меньше Т_кр, то есть тем меньше его температура Кюри Т_см (Т_кр = Т_см).

С другой стороны у парамагнетиков и более сильных ферромагнетиков магнитное поле Н совпадает с направлением движения электрического тока, а так называемый (виртуальный) "ток смещения", то есть возникающее диамагнитное противополе самоиндукции В при нормальных температурах относительно мало. Поэтому электромагнитное сопротивление току не велико. Чем больше В (при В<Н), тем больше абсолютное электросопротивление R (или удельное сопротивление ?). При В=Н, стремящийся прохождению по образцу ток мгновенно прекращается и материал становится не токопроводящим, то есть диэлектриком (изолятором). Если В>>Н, то это не "сверхпроводник", а по существу абсолютный диэлектрик (изолятор) и сверхдиамагнетик. Эти утверждения автора обосновываются в данной монографии.

В качестве примечания отметим, что, с точки зрения автора, на рисунках 2, 5, 25 и 26 и в поясняющих их текстах, взятых из литературных источников, где указаны R надо было бы писать U - разность электрических потенциалов или Н - напряженность магнитного поля, так как фактически R получены или пересчетом экспериментально измеренных значений U или простой подменой U и H на R.

Проблеме "сверхпроводимости" электрического тока уже больше 100 лет. За такой срок не решаются только заведомо ложные проблемы.

Итак, общее резюме вышеизложенного состоит в том, что решение проблемы "сверхпроводимости" электрического тока состоит в признании фактического отсутствия этой проблемы, так как не существует "сверхпролводимости" электричества с нулевым сопротивлением, а вместо этого есть объективное и теоретически адекватно объяснимое явление сверхдианамагничивания (сверхантиферронамагничиваемости) и изоляции (диэлектризации) веществ в условиях меньше запредельно низкой температурной точки Кюри.

Далее этот вывод доказывается при анализе экспериментов и теорий "сверхпроводимости".

2. ФАКТЫ И ИХ ИНТЕРПРЕТАЦИИ

2.1 Первые опыты Оннеса

Считается, что в 1911 году голландский ученый Хейке Камерлинг-Оннес (кратко Оннес) с сотрудниками обнаружили сверхпроводимость, то есть явление проводимости металлами электрического тока без сопротивления при температурах близких к абсолютному нулю. Однако были и остаются сомнения в том, что все-таки открыл Оннес. Он и сам вначале колебался в объяснениях обнаруженного им эффекта быстрого, резкого падения, вплоть до исчезновения, разности электрических потенциалов на концах у охлаждаемого проводника с током при критической температуре, соответствующей его внутренней природе.

Сотрудники Оннеса, участвующие в экспериментах по измерению электрических свойств проводников при температурах жидкого гелия [114.С.6], в своих публикациях достаточно подробно описали методику проводимых измерений [129,130].

В работе [130] констатируется, что в начале 19-го века "было известно, что электрическое сопротивление в металле уменьшается с понижением температуры... Лорд Кельвин полагал, что поток электронов, по-видимому, улучшается с уменьшением температуры, что приводит к более низкому значению сопротивления, но он может фактически остановиться, а электроны становятся как бы замороженными на месте. Сопротивление при абсолютном нуле температуры, таким образом, было бы бесконечно высоким. Другие, включая Оннеса и Дьюара, предполагали, что уменьшение сопротивления при понижении температуры продолжается, в конечном счете достигая нуля в точке нулевой температуры... То, что фактически случилось, было ошеломляющим и, учитывая понимание вопроса на атомном уровне в 1911г., полностью непредсказуемым" [130.С.98].

Первый эксперимент по измерению показаний электрического тока при криогенных температурах был осуществлен на образце из ртути. "Гиллес Холст, который выполнил измерения, использовал U-образную капиллярную стеклянную трубку, в обоих концах которой были платиновые электроды, и она была заполнена очищенной жидкой ртутью при комнатной температуре. Измерения электрического сопротивления (гальванометром - В.Ф.), проведенное с успехом в температурных диапазонах жидкого кислорода, жидкого азота и жидкого водорода, показали известное регулярное уменьшение. При температуре жидкого гелия, однако, Холст обнаружил нулевое сопротивление, которое вначале приписывали короткому замыканию где-нибудь в криостате. Измерение было повторено несколько раз..., но каждый раз обнаруживалось предполагаемое короткое замыкание" [129.С.41]. Последующие эксперименты с зигзагообразными образцами показали, что короткого замыкания нет. По-видимому, из этого факта Оннес сделал поспешный и необоснованный вывод о том, что ток в образце течет без сопротивления, так как нет у него разности электрических потенциалов. Обнаруженный эффект исчезновения разности потенциалов Оннес вначале назвал супрапроводимостью, а позднее суперпроводимостью.

Это свое объяснение исчезновения разности потенциалов на участке проводника из твердой (замороженной) ртути Оннес незамедлительно и единолично опубликовал в ноябре 1911 года [131].

Кстати, "несмотря на то, что впервые абсолютное падение напряжения по показаниям гальванометра наблюдал Г.Холст, сделавший решающее измерение, он не был соавтором ни одной из ранних публикаций, которые следовали из работы с Камерлинг-Оннесом" [130.С.99]. Имя Г.Холста не упоминалось и в достаточно подробной Нобелевской лекции, прочитанной Хейке Камерлинг-Оннесом 13 декабря 1913 года [113]. В отношении этого факта В.Л.Гинзбург писал: "Впервые ясное и вполне определенное наблюдение сверхпроводящего перехода было сделано в Лейденской лаборатории производившим измерения Г.Холстом (Gilles Holst). Это был квалифицированный физик... Однако в статье Камерлинг-Оннеса [131], в которой сообщается об этих измерениях, имя Холста даже не упоминается. Не представляю себе, чтобы в наше время нечто подобное могло произойти в цивилизованной стране (впрочем, возможно я и ошибаюсь)" [31.С.113].

Из публикаций коллег Оннеса [129,130] следует, что измерения электрического тока производили зеркальным (световым) гальванометром. Это важно учитывать при выяснении того, что всё-таки измеряли гальванометром: электрическое сопротивление току или напряжение на концах проводника. Сам Оннес писал: "К концам резисторов присоединены ртутные нити, чтобы проводить ток и измерять разность потенциалов" [113.С.231]. Однако тут же утверждает, что "опыт не оставляет сомнений в том, что сопротивление в пределах погрешности измерений исчезло... Таким образом, при 4К ртуть перешла в новое состояние, которое, благодаря его особенным электрическим свойствам, можно назвать состоянием сверхпроводимости" [113.С.233]. В статье Р.Б.Оуботера читаем, что люди, проводившие измерения "сидели в темной комнате на расстоянии 50 метров, делая записи считываний сопротивления от гальванометра" [130.С.101]. Я.Нобель констатировал: "Холст, сидевший в центральной темной комнате, в которой были расположены несколько гальванометров лаборатории, увидел, что пучок света его гальванометра внезапно отклонился... И таким образом сверхпроводимость была обнаружена..." [129.С.42].

Приведенные выше сведения из цитат свидетельствуют, что измерения "электросопротивления" производились простыми зеркальными (световыми) гальванометрами.

Известно, что зеркальный гальванометр является высокочувствительным магнитоэлектрическим прибором для измерения электрического тока. Работа данного прибора основана на действии постоянного магнита на катушку в виде прямоугольной рамки по которой идет измеряемый тока [47]. В этом гальванометре используется подвес подвижной рамки с током на упругой нити (металлической или кварцевой). Измерительная система такого прибора имеет световой усилитель, то есть указательная стрелка заменена лучом света от специального источника. Этот луч, отразившись от зеркальца, закрепленного вблизи подвижной рамки, попадает на измерительную шкалу. Шкала устанавливается на расстояние 1м от зеркальца. Следовательно, световой указатель (световое пятно на шкале) эквивалентен стрелке длиной 1м. Благодаря этому малому отклонению подвижной зеркальной части соответствует большое перемещение светового указателя на шкале измерения.

Использование нитевой подвески и светового указателя придает зеркальному гальванометру повышенную чувствительность не только к изменениям измеряемой величины, но и к любым внешним механическим, электромагнитным и другим воздействиям на него. С целью устранения негативных причин неточности измерений зеркальный гальванометр устанавливают строго горизонтально (по уровню) и перед измерением обязательно производят балансировку и юстировку измерительной системы этого прибора, что свидетельствует о недостаточной стабильности и, следовательно, точности его показаний.

Измерение зеркальным потенциометром осуществляется посредством определения угла закручивания ? подвижной части измерительного механизма и его зеркала. Крутящий момент подвижной части прибора равен:

где I - ток или электродвижущая сила (э.д.с.);

k_кр - коэффициент пропорциональности.

Механический момент противодействия М_пр повороту подвижной части со стороны нити подвеса таков:

где k_пр - соответствующий коэффициент пропорциональности.

Измеренная величина определяется когда М_к_р = М_пр, то есть когда k_крI = k_пр?. Следовательно, измеряемая гальванометром величина интегрального показателя электрического тока I будет равна:

здесь k - переводной коэффициент шкалирования по эталону.

Так по величине ? судят о значении I пропорциональном разности электрических потенциалов или о напряжении U на исследуемом участке цепи, так как:

где G - коэффициент пропорциональности, называемый показателем проводимости (G=1/R);

?_max и ?_min - электрические потенциалы на концах проводника;

R - коэффициент, характеризующий сопротивление электрическому току;

U - разность (падение) потенциалов или напряжение на измеряемом участке электрической цепи.

Из вышеизложенного следует, что простым зеркальным (или световым) гальванометром (при последовательном его включении в сеть) измеряют небольшую силу тока I, а при наличии энергетических потерь тока гальванометром, подключенным (как было у Оннеса) параллельно участку электрической цепи, измеряет разность потенциалов на участке проводника, т.е. ?_max - ?_min, которая является электрическим напряжением U между двумя точками на измеряемом проводнике.

Методика обработки результатов измерений "сопротивления" состояла у Оннеса в сопоставлении условных показателей разности потенциалов (оцениваемой по ?) исследуемого проводника при температуре 0®С с аналогичной разностью потенциалов при низких температурах, например, при 4,2К [113.С.231]. На соответствующих графиках в публикациях [112,113], оцененное по ?U "сопротивление" в долях от "сопротивления" проводника при обычной температуре, должно быть выражено в милливольтах, а не в Омах. Заметим, что для измерения проводимости G или сопротивления R одного гальванометра не достаточно: нужен ещё и амперметр. Гальванометром электросопротивление не измеряют. Непосредственно электросопротивление измеряют омметром. Разность потенциалов не тождественна электросопротивлению, да и размерность у них разная.

Уже на основании вышеизложенного можно утверждать, что результаты опытов Оннеса и его коллег по "замерам электрического сопротивления гальванометром" не верны и поэтому доказательство открытия явления "сверхпроводимости" ошибочно.

По законам физики и по мнению самого Оннеса "необходима разность потенциалов, чтобы поддерживать ток" [113.С.234]. Следовательно, при отсутствии у проводника разности потенциалов (электрического напряжения), как в случае со "сверхпроводимостью", в "сверхпроводнике" не может быть ни тока, ни сверхтока, тем более переносящего электрическую энергию абсолютно без сопротивления.

Очевидно, что по сути дела Оннесом и его сотрудниками была обнаружена не "сверхпроводимость", а другое по физической природе явление, а именно переход токопроводящих материалов при закритически низких температурах в абсолютно диэлектрическое (не токопроводящее) состояние, то есть, наоборот, обнаружен переход металлов в состояние изолятора, а не в состояние сверхпроводимости [109].

Оннес в своей Нобелевской лекции сообщал: "Уже после самых первых экспериментов на сопротивление металлов мы получили удивительные результаты. В случае с платиновой проволокой не было нового возрастания сопротивления после достижения минимума, как этого можно было ожидать, если бы электроны, обеспечивающие проводимость, были бы сильно приморожены к атомам при низких температурах, но, наоборот, сопротивление перестало зависеть от температуры. Вывод, сделанный из результатов эксперимента, проведенного вместе с господином Клейем, ... состоял в том, что в абсолютно чистой платине сопротивление исчезает в точке кипения гелия. Поэтому при самых низких температурах проводящие электроны не будут связаны, а факторы, мешающие их движению, исчезнут" [113.С.230]. "Тот факт, что сопротивление равнялось некоей константе, а не нулю, я приписывал незначительным примесям, даже в чистом золоте" [113.С.231]. "Как уже говорилось, опыт не оставляет сомнений в том, что сопротивление в пределах погрешности измерений исчезло. Но в то же время появилось нечто неожиданное. Исчезновение происходило не постепенно, а резко. От 1/500 сопротивление падает до одной миллионной при температуре 4,2К. При более низкой температуре (1,25К) можно констатировать, что сопротивление стало меньше, чем одна миллионная от сопротивления при нормальной температуре. Таким образом, при 4К ртуть перешла в некое иное состояние, которое, благодаря его особенным электрическим свойствам, можно назвать состоянием сверхпроводимости" [113.С.233] или "супра-проводящим состоянием" [112.С.26]. "К концам сопротивления из ртутной проволоки прикреплялась разветвленная система проволок из одного металла для того, чтобы проводить ток и измерять разность потенциалов" [113.С.231].

Из вышеприведенных цитат следует, что Оннес всегда измерял не сопротивление току с помощью омметра, а оценивал его как-то опосредствованно, то есть по результатам измерения разности электрических потенциалов на концах исследованного проводника, что не равнозначно и поэтому ошибочно. При этом Оннес считал, что уменьшение разности электрических потенциалов свидетельствует исключительно только об уменьшении сопротивления току. Однако можно считать и так, что уменьшение разности потенциалов ведет к уменьшению тока за счет увеличения электрического сопротивления при понижении температуры вследствие усиления диамагнитного поля испытуемого проводника.

Дело в том, что сопротивление электрическому току зависит не только от температуры проводника, но и от его диамагнитной и, следовательно, диэлектрической проницаемостей и восприимчивостей. Было известно и самому Оннесу, что у проводника с током есть тепловое и холодное диамагнитное сопротивление электрическому току. Это диамагнитное сопротивление возникает от индукции током диамагнитного поля B, направленного против магнитного поля H электрического тока I.

Описывая работы по магнетизму супра-проводников, Оннес указал, что в одной работе доктора Бекмана, показано "до каких больших значений доходит магнитное сопротивление висмута при водородных температурах" [112.С.10]. И далее: "После открытия Вейесом магнетона результаты этой работы послужили для определения этой величины, которая, по-видимому, имеет важное значение для магнитных моментов всех атомов. Произведенное Перрье и мною исследование жидкого и твердого кислорода указало на отклонение закона Кюри, найденные нами затем и у парамагнитных солей. Продолжение этой работы с Остергейсом показало, что часть этих отклонений может быть объяснена молекулярным Вейесовским полем с отрицательным знаком" [112.С.11], то есть диамагнетизмом.

Отметим сразу же, что поле с "отрицательным знаком", создающее "магнитное сопротивление" электрическому току, и доходящее до "больших значений", это ничто иное как индуцируемое электрическим током диамагнитное поле проводника B.

Очевидно, что электросопротивление R и разность электрических потенциалов на концах исследуемого проволочного проводника являются разными, хотя и взаимно зависимыми, характеристиками. Поэтому нельзя считать, что разность потенциалов однозначно характеризует электросопротивление. Разность потенциалов и электросопротивление зависят от количества электричества (от электрического тока) I, проводимого данным проводником. Естественно, чем больше R, тем меньше электрический потенциал тока на входе его в исследуемый участок проводника и тем меньше I. Следовательно, разность потенциалов зависит от R, I и от начального электрического потенциала ?_н на входе тока в проводник. Поэтому ошибочно было и остается утверждение о том, что по разности потенциалов можно однозначно определять величину и исключительно только электросопротивления проводника. Однако Оннес отождествлял, а его последователи, признающие сверхпроводимость электрического тока при закритически низких температурах, до сих пор считают, что понятия о разности потенциалов и об электросопротивлении являются почти синонимами и поэтому взаимозаменяемыми.

Оннес, указывая на существование для сверхпроводимости порогового значения тока, "которое находится тем выше, чем ниже температура", определил, что "при токах меньше этого значения на концах резистора нет разности потенциалов ... Но как только превышается это пороговое значение, необходима разность потенциалов, чтобы поддерживать ток. Тогда возникает (и это еще не объяснено) обычное сопротивление в проволоке" [113.С.234]. Здесь у Оннеса явная путаница. Не разность потенциалов нужна для тока, а входной потенциал электродвижущей силы (э.д.с.). Электрический ток и сопротивление ему создают разность потенциалов. Разность потенциалов есть следствие сопротивления, а не наоборот, как очевидно считал Оннес. Поэтому отсутствие разности потенциалов на концах "сверхпроводящей" проволоки свидетельствует об отсутствии в ней электрического тока. Такое объяснение эффектам, обнаруженным Оннесом и его сотрудниками, представляется естественным и не противоречащим теории электричества. Оннес правильно утверждал, что в случае с его "сверхпроводимостью" электрического тока, которого нет в "сверхпроводнике", "закон Ома теряет свою силу" [113.С.235], что вполне очевидно. Закон Ома написан исключительно для электрического тока. Если нет разности электрических потенциалов на концах проводника, то это означает, что нет в нем ни тока, ни сопротивления ему. Удивляет, как в таком случае можно было сделать вывод не об отсутствии тока, а о его сверхпроводимости. Спрашивается, почему ученые поверили очевидно ошибочному утверждению Оннеса о "сверхпроводимости" электрического тока с нулевым сопротивлением при закритически низких температурах? Очевидно, что если у "сверхпроводника" нет разности электрических потенциалов (напряжения), и не действует закон Ома, то есть ничего нет, то невозможно определить значения электросопротивления и тока, так как их нет в проводнике. Только такой вывод следует из опытов Оннеса.

Считается, что Оннес обнаружил еще один чудесный эффект "сверхпроводимости", суть которого состоит в "обнаружении незатухающих токов" [113.С.211], что дает возможность создания вечного двигателя. Но очевидно, что обнаруживалась незатухающая намагниченность, а не вечный электроток.

Вот какие у Оннеса доказательства "незатухающих токов". В публикации его Нобелевской лекции читаем: "Рассмотрим пример: замкнутый контур, охлажденный в магнитном поле, должен, если убрать поле, некоторое время имитировать амперный молекулярный ток... В полях ниже порогового значения, которое так и не было достигнуто во время опыта с маленькой катушкой, магнитного сопротивления не было вообще. В течение экспериментов, связанных с токами, сохраняющимися в сверхпроводниках в отсутствие электродвижущей силы, было достигнуто следующее. Ток, однажды порожденный, не прекращался часами, практически не меняясь в сверхпроводимой фольге" [113.С.235-236].

По данным Оннеса "в контуре наведенное постоянное магнитное поле не убывает после того, как убирали магнит от "сверхпроводящего контура". С другой стороны, в "сверхпроводнике" с током после отключения тока он не прекращался часами, практически не меняясь. Это и есть "незатухающие токи". Однако следует заметить, что о токах Оннес судит по наличию магнитного (точнее диамагнитного) поля вблизи "сверхпроводника". Из опытов Оннеса, а в последствие и других аналогичных опытов других авторов, следует только один правильный вывод: "сверхпроводники" сильно дианамагничиваются под влиянием внешнего магнитного и электромагнитного полей. Поэтому после удаления магнита от переохлажденного в жидком гелии проводника или после отключения его от источника постоянного тока в проводнике (названного ошибочно "сверхпроводником") всегда и долго сохраняется дианамагниченность, а не мистический электрический ток.

2.2. Анализ существующих объяснений эффекта "сверхпроводимости" электричества

Результаты первых исследований низкотемпературного электросопротивления платины и ртути Оннес опубликовал в 1911 г. В его статьях было показано большое уменьшение сопротивления платины, золота и ртути при сверхнизкой температуре жидкого гелия. Экстраполируя полученные данные до 0 К, Оннес высказал предположение о "сверхпроводимости", в частности, твердой (закристаллизовавшейся) ртути как наиболее чистого от примесей металла. Позднее в статье, написанной Оннесом к Третьему Международному конгрессу по низким температурам, состоявшемуся в сентябре 1913 г. в городе Чикаго, он написал: "Я уже склоняюсь к мнению, высказанному Дьюаром, что сопротивление должно стремиться к нулю при абсолютном нуле температуры, но результаты опытов при температуре жидкого гелия оказались совершенно неожиданными. Сопротивление очень чистой платины становится постоянным вместо того, чтобы проходить через минимум или бесконечно уменьшаться при стремлении температуры к абсолютному нулю". О предельных значениях уменьшения обычного электросопротивления при понижении температуры сплавов было известно, и объяснялось это наличием в них примесей. Считая, что только примеси препятствуют исчезновению сопротивления платины и, возможно, золота, Оннес решил производить опыты "с единственным металлом, из которого можно надеяться получить проводники самой высокой степени чистоты, а именно - с ртутью... Заранее можно было сказать, что сопротивление проводника из твердой ртути будет иметь измеримую величину при температуре кипения гелия, но упадет до ничтожной величины при более низких температурах, которых я мог бы достигнуть. Имея перед собой такую великолепную перспективу, можно было не считаться с трудностями. Они были преодолены, и результат опытов оправдал все ожидания. Не осталось сомнения в существовании нового состояния ртути, в котором сопротивление фактически исчезает... Ртуть перешла в новое состояние, которое в соответствии с его необыкновенными электрическими свойствами можно назвать сверхпроводящим состоянием" [119.С.9-10].

Позднее сам Оннес определил, что добавление к ртути значительного количества примесей не препятствует "падению сопротивления до нуля".

В первых своих опытах Оннес использовал потенциометрический метод расчетного определения величины электросопротивления, пропуская по платиновой проволоке, охлажденной до гелиевых температур, постоянный электрический ток (рис. 1, а). Позднее Оннес и другие исследователи стали использовать магнитометр для фиксации магнитного поля, а не электрического тока в "сверхпроводнике" (рис. 1, б, в).

а б в

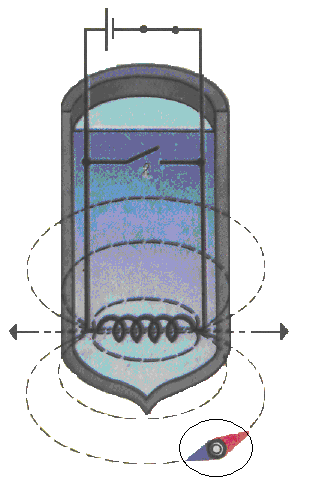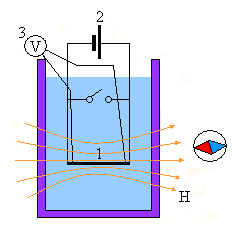
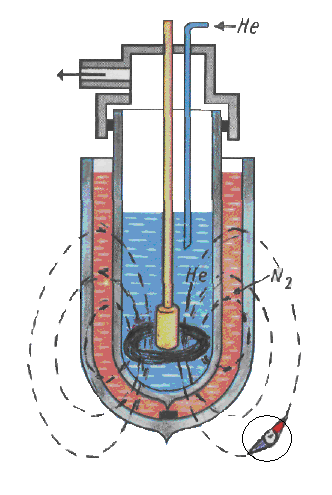
Рис. 1. Схемы обнаружения "сверхпроводимости":

а - обычная схема измерения малых электросопротивлений

(1 - исследуемый проводник, 2 - источник постоянного тока,

3 - микровольтметр);
б - измерение магнитного поля кольцеобразного образца;
в - измерение магнитного поля замкнутого

контура только магнитометром (магнитной стрелкой)

Анализируя приведенные схемы обнаружения "сверхпроводимости", можно видеть, что они не являются прямыми доказательствами существования "сверхпроводимости" электрического тока.

В схемах а и в активные электросопротивления внутри дюара с гелием в случае R=0 создают эффект короткого замыкания электрической цепи, при котором невозможно возникновение и существование "сверхпроводимости" с неограниченно большой силой тока (см. закон Ома). Последствия короткого замыкания для проводника и источника постоянного тока (батареи или аккумулятора), когда R?0, известны. При переходе проводника от нормальной проводимости (R>0) к "сверхпроводимости" (R=0), т. е. при резком падении электросопротивления (R?0), так же резко должен возрастать электрический ток проводимости (I??), а напряжение в сети от источника тока столь же интенсивно должно уменьшаться (U?0). При резком увеличении интенсивности тока, даже при аналогичном уменьшении удельного электросопротивления ?, у реального провода плотность электрического тока также увеличивается и тепловыделение существенно возрастает. Поэтому переход провода в "сверхпроводящее" состояние при передаче им сверхсильно возрастающего электрического тока, даже при изначально очень маленьком электросопротивлении, не может происходить, во-первых, одномоментно - скачкообразно; во-вторых, известно, что токи больше некоторого критического значения разрушают наведенную "сверхпроводимость". Поэтому при R?0 и I?? "сверхпроводимость" не может возникнуть из-за закритически большого электрического тока в "сверхпроводнике".

В связи с проблемой "сверхпроводимости" обратимся к вышеупомянутому закону Ома. Он, как хорошо известно, формулируется, для участка проводника с током, так: "электрический ток I, идущий в проводнике, численно равен отношению падения электрического потенциала U = ?₁ - ?₂ (где ?₁ и ?₂ - электрические потенциалы в начале и в конце данного участка проводника), которое часто называют напряжением и обозначают буквой U, к сопротивлению проводника R току I, то есть:

0x01 graphic
.

Сопротивление конкретного проводника R зависит от его геометрических размеров и формы, а также от химического состава и внутренней структуры материала, из которого сделан проводник" [47.С.94].

Заметим, кстати, что падение напряженности электрического тока ?₁ - ?₂ = U обусловлено, то есть зависит от ?₁ и от сопротивления проводника R току I. И U и R характеризуют по-разному, но одно и то же - сопротивляемость проводника току I. Чем больше R, тем больше U и наоборот. Следовательно, со смысловой (физической) точки зрения, величину U, существенно зависящую от R, делить на R не вполне корректно.

Закон Ома в изложенной выше редакции используется при соблюдении следующих условий: при постоянной температуре проводника, без его деформации и при отсутствии или при неизменяющихся, проникающих извне, облучениях и др.

Если при каких-либо внешних воздействиях на проводник изменяется его внутреннее состояние, то R обычно увеличивается или уменьшается. Очевидно, что при снижении температуры проводника и при уменьшении его сопротивления R разность потенциалов U тоже уменьшается. Но при этом, исходя из формулы закона Ома, ток I может остаться неизменным, увеличиваться или уменьшаться. Это зависит от изменения соотношения U и R.

Возможен и другой процесс. Если при понижении температуры проводника его сопротивление возрастает (как, например, у полупроводников), то есть при отрицательном температурном коэффициенте сопротивления (ТКС), то разность потенциалов (при постоянном ?₁) тоже увеличивается. Но, как и на сколько изменится ток опять-таки зависит от скорости (величин) изменения U и R.

Исходя из вышеизложенного, следует, что при R=0 и U=0. В экспериментах измеряемое падение электрического напряжения на участке "сверхпроводника" всегда равно нулю, то есть U=0. Поэтому очевидно, что при U=0 и даже если R=0, то получаем

0x01 graphic
,

и, следовательно, бывший проводник становится не сверхпроводником, а диэлектриком (изолятором). Получается, что ток "сверхпроводимости" равен нулю - его просто нет.

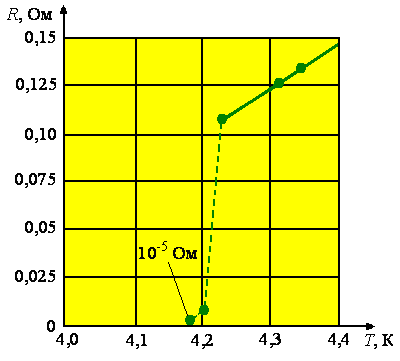
Если же при понижении температуры электросопротивление проводника возрастает до соответствующего, блокирующего ток, значения R_бл, то ток прекращается и U=0. То есть U=0 не означает, что и R=0. В рассматриваемом случае при U=0 значение R™R_бл, а 0x01 graphic

В обоих рассматриваемых случаях при U=0 тока вообще и тока "сверхпроводимости" в частности, быть не может - проводники становятся диэлектриками (изоляторами).

В "сверхпроводниках" тока нет, нет электросопротивления, нет и выделения тепла. Академик Л. Д. Ландау не случайно по этому вопросу писал, что необычный "сверхпроводящий ток не должен переносить тепла. Это подтверждается известным фактом отсутствия термоэлектрических явлений в сверхпроводниках" [61.Т.2.С.380]. Тока "сверхпроводимости" нет, а что есть? Есть то, что измеряется во всех экспериментах со "сверхпроводимостью" - есть сильное дианамагничивание материалов.

Почему-то приверженцы идеи "сверхпроводимости" считают, что электричество в проводнике, имеющем сверхнизкую температуру, может возникнуть (индуцироваться) сверхток и куда-то течь под воздействием постоянного магнитного поля. Это утверждение антинаучно, так как противоречит электродинамике и практике. Постоянное магнитное поле не индуцирует дополнительный электрический ток. Оно может только намагничивать объект своего воздействия. Следовательно, в опытах с кольцами (см. рис. 1, б) мы имеем дело с намагничиванием, а не с электропроводностью в них.

С другой стороны, представляется необъяснимым, как это возможно, что в абсолютно замкнутом однородном кольцеобразном контуре (в кольце) будто бы может возникнуть электрический ток (при статических условиях влияния на кольцо каким-либо магнитным полем) и постоянно протекать там даже в отсутствие внешнего индуцирующего магнитного поля, если по условиям эксперимента во всех точках кольца действительно возникнет одинаковый электромагнитный потенциал напряжения. Однако известно же, что электрический ток всегда движется в направлении от большего к меньшему напряжению, а при постоянном напряжении в любом проводнике, в том числе и в кольцеобразном, тока (т. е. движения электрической энергии) нет и быть не может. Следовательно, утверждения о том, что в экспериментах с кольцами в них есть неуменьшающийся ток "сверхпроводимости", противоречит научным фактам и уже поэтому являются неадекватными и антинаучными.

Итак, уже изначально, т. е. с первых экспериментов по мнимой "сверхпроводимости", объяснение их результатов противоречит другим научным фактам, логике и здравому смыслу.

Констатируется очевидное: если измеряемое сопротивление проводника электрическому току равно нулю, т. е. электросопротивления нет, то это в первую очередь означает, что в проводнике нет электрического тока, проводнику нечему сопротивляться, поэтому нет искомого электросопротивления. Наличие же наведенного диамагнитного поля есть эффект дианамагничивания вещества в результате прохождения по нему постоянного электрического тока с его постоянным электромагнитным полем или же в результате воздействия на вещество внешнего постоянного магнитного поля. Утверждение о том, что после отключения постоянного электрического тока в "сверхпроводнике" действительно R=0, а наведенное магнитное поле остается неизменным, убедительно свидетельствует об отсутствии в проводнике электрического тока, а также о намагниченности проводника и других веществ при описанных выше условиях экспериментов. Следовательно, в данном случае нужно говорить не о сверхпроводимости электричества, а о переходе ферромагнитных, парамагнитных и немагнитных тел к диамагнитному и, соответственно, к диэлектрическому состоянию. Вполне вероятно, что наведенное диамагнитное поле, противодействуя другим полям, запирает обусловленное ими прохождение по телу постоянного электрического тока.

Кстати, возможно, что этот же эффект "запирания", т. е. непропускания той части переменного тока, которая не совпадает (противоположно направлена) с возникающим диамагнитным полем соответствующего полупроводника, проявляется в выпрямителях и усилителях переменного электрического тока. Есть основания предполагать, что физическая природа "запирания" части переменного электрического тока в полупроводниковых выпрямителях имеет не электростатическую, не зарядовую сущность (p-n-переход), а магнитную (магнитно-диамагнитный переход). Разработка магнитной теории твердотельных выпрямителей переменного тока не является первоочередной задачей. Однако имеющийся практический опыт создания мощных полупроводниковых выпрямителей, а также биполярных и иных приборных транзисторов, с учетом их магнитной физической природы взаимодействия с электрическим током, вероятно, позволит создать материалы со сверхдианамагничиваемостью при комнатных и более высоких температурах.

Вернемся к "сверхпроводимости" и подробнее рассмотрим опыты Оннеса. При потенциометрическом (косвенном) измерении (см. рис. 1, а) электросопротивление рассчитывается по показаниям миллиамперметра и гальванометра (милливольтметра) на основании известного закона Ома. При определении очень малых значений электросопротивления точность и чувствительность измерительных приборов должны быть очень большими. Возможно, что измерительные приборы, используемые Оннесом тогда (в 1911 г.), еще не имели достаточной чувствительности и точности для измерения сверхмалых величин параметров электрического тока (силы тока I и напряжения U). Вероятно, что, дойдя до пределов чувствительности миллиамперметра и гальванометра, Оннес не смог измерить остаточное электросопротивление ртути при температурах ниже 4,2 К. Этот "нулевой" результат инструментального происхождения мог быть ошибочно воспринят Оннесом как полное отсутствие электросопротивления у твердой ртути при ее глубоком переохлаждении до температур ниже 4,2 К.

В ряде литературных источников, например в [41] и [114], приводится как-то рассчитанная Оннесом зависимость электросопротивления ртути от уменьшения температуры (рис. 2).

0x01 graphic

Рис. 2. Предполагаемая Оннесом зависимость электросопротивления ртути от температуры [79]

Можно утверждать, что обозначенные Оннесом значения электросопротивления ртути в 10^-5 Ом при температурах ниже 4,2 К находятся в пределах постоянной ошибки измерений, обусловленной погрешностью приборов и неточностью методики измерений. Не случайно у Оннеса получился как бы "скачкообразный" переход к "практически нулевому" сопротивлению электрическому току. В этом отношении можно привести много примеров аналогичных "скачков". Скачкообразно, резко происходят кристаллизация чистых металлов и их плавление при постоянной (критической) температуре, но на протяжении некоторого времени. Тут, как и в опытах Оннеса, "скачок" не во времени, а в различии состояний, в факте перехода из одного состояния в другое.

Первоначально Оннес утверждал, что при критической температуре сопротивление току падает, по крайней мере, в 10⁶ раз. Позднее сам Оннес и Р. Грассман показывали, что электросопротивление в "сверхпроводящем" состоянии составляет меньше 10^-12 сопротивления образца непосредственно над точкой перехода. А еще позднее Оннес и его последователи стали утверждать, что электросопротивление у многих металлов при гелиевых температурах исчезает вовсе, оно равно нулю (R=0). Это невероятное до сих пор мнение утвердилось в среде ученых-физиков после других экспериментов Оннеса и иных ученых с кольцеобразными проводниками. Но "экспериментально установить, что электросопротивление, равное нулю (?=0), принципиально невозможно. Можно лишь утверждать, что значение ? меньше некоторого значения, определяемого точностью измерения" [9.С.332-333].

Видимо, зная, что способ прямого потенциометрического измерения электросопротивления недостаточно точен и сложен, Оннес разработал и широко использовал другой достаточно простой метод исследования электромагнитных свойств металлов, заключающийся в наблюдении за возможным затуханием характеристик магнитного поля, наведенного в кольцеобразном образце. Этот электромагнитный метод заключается в предположении, что индуцируется электрический ток в замкнутой цепи (кольце) под воздействием внешнего магнитного поля. Этот ток сопровождается возникновением магнитного поля внутри и вокруг проводника, которое регистрируется (измеряется) при помощи магнитометра. После устранения внешнего магнитного поля в переохлажденном кольце сохранялось неопределенно долго наведенное магнитное поле, намного большее, чем наводящее. Этот факт был воспринят как незатухание электрического тока из-за отсутствия электросопротивления. Сохранение магнитного поля исследуемого образца после отключения электрического тока или после устранения внешнего магнитного поля было, как уже отмечалось, необоснованно названо Оннесом сверхпроводимостью электрического тока, а не сверхнамагничиваемостью.

Если же объективно, т. е. по результатам измерений, изобразить на графике обнаруженный Оннесом эффект, то его следует строить (в отличие от графика на рис. 2) в экспериментально измеряемых координатах: напряженность наведенного магнитного поля H и температура T. В таком случае нельзя говорить об электрической сверхпроводимости - несопротивляемости электрическому току. Наиболее вероятно, что обнаруженный эффект Оннеса является эффектом максимальной намагниченности, или сверхнамагничиваемости. Вопрос о правильности, об адекватности названия эффекта Оннеса будет еще подробно рассматриваться в данной публикации.

В апреле-июне 1914 г. Оннес продемонстрировал, что якобы ток, возбужденный однажды в замкнутом контуре при температуре ниже критической температуры Т_кр, не только практически не имеет электросопротивления, но и не ослабевает со временем. Несколько позднее в качестве доказательства своих умозаключений он перевез "сверхпроводящее кольцо с текущим по нему током из голландского города Лейдена в английский Кембридж" [119.С.6]. При проверке этого явления в СССР оказалось, что, действительно, магнитное поле, наведенное в сверхпроводящем кольце, сохранялось без изменения в течение более двух лет (март 1956 - сентябрь 1958 г.). Эксперимент этот был прекращен, так как дальнейшее его проведение стало нецелесообразным из-за больших затрат средств. Было оценено, что время, требуемое для исчезновения обнаруженного эффекта, составляет не менее 100 000 лет. В иностранной литературе имеются сведения о десятилетнем эксперименте с тем же результатом.

Открытое Оннесом явление, названное сверхпроводимостью, вот уже почти 100 лет активно исследуется. Однако физическая природа и сущность этого явления до сих пор остаются непонятыми, дискуссионными.

Полагаю, что прежде чем заявить (опубликовать) об открытии явления "сверхпроводимости", тем более как сенсационного открытия, автору необходимо было привести убедительные, неопровержимые доказательства. Для этого надо было осуществить дополнительные контрольные, уточняющие эксперименты. Эти эксперименты должны не косвенно, а непосредственно демонстрировать сверхсильную проводимость электрического тока. Так, например, Оннес, утверждая о "сверхпроводимости" электрического тока мог бы убедить всех непосредственными наблюдениями "сверхпроводимости" именно электрического тока. Для этого, например, необходимо взять "сверхпроводниковую" проволоку, но находящуюся в обычном состоянии проводимости, то есть при комнатной температуре, и с ее помощью составить электрическую цепь постоянного тока с последовательным включением в нее электрической лампочки накаливания. Лампочка будет гореть. Но если потом часть провода охладить в жидком гелии и дождаться пока материал перейдет в "сверхпроводящее" состояние. В связи с переходом охлажденной части проволоки в диамагнитное состояние, лампочка, затухая, погаснет. Этот факт был бы прямым доказательством прекращения электрической проводимости, и что охлажденная часть провода стала диэлектриком (изолятором). Но если лампочка в конце эксперимента будет гореть намного ярче, то это было бы непосредственным подтверждением "сверхпроводимости" охлажденного участка провода. В подобном эксперименте вместо охлаждаемого участка "сверхпроводниковой" проволоки можно использовать "сверхпроводниковый" образец в виде цилиндра или проволоки. Однако таких экспериментов не было сделано и, следовательно, провозглашение "сверхпроводимости" не является обоснованным. Фиксированное Оннесом отсутствие разности электрических потенциалов на краях испытываемого образца не может приниматься за факт "сверхпроводимости" поскольку при этом не наблюдалась даже малая проводимость электрического тока. Фактом здесь является намагничиваемость испытываемого образца.

В наши дни утверждается, что даже керамические материалы, то есть изоляторы, становятся "сверхпроводниками", но II рода. Следовало бы проверить так ли это. Для этого так же керамический образец из "сверхпроводника II рода" надо последовательно соединить обычным проводником (например, медной проволокой) с электрической лампочкой (или с другим нагревательным устройством способным фиксировать прохождение электрического тока, а не магнитное поле) и подключить к источнику постоянного тока. При этом лампочка гореть не будет. Но если образец охладить в жидком азоте, то есть перевести его в "сверхпроводящее" состояние, то, как следует из "теории сверхпроводимости" лампочка должна загореться. К сожалению, о такого рода экспериментах в общедоступной литературе нет информации возможно потому, что лампочка не загорается и это опровергает современную "теорию сверхпроводимости". Такие "отрицательные" результаты обычно признаются просто неудачными и придаются забвению. Но в науке всякие результаты важны для создания адекватной, объективной, истинной теории исследуемого явления.

Доказывая "сверхпроводимость" Оннес и его последователи, очевидно, исходили из правильного соотношения, что проводимость электрического тока G обратно пропорциональна электросопротивлению R конкретного проводника, то есть

0x01 graphic
.

Удельная проводимость электричества ? также обратно пропорциональна удельному электросопротивлению ?:

Если считать, что при "сверхпроводимости" R=0 и ?=0, то в таком случае чему будут равны 0x01 graphic

и
? По существующим математическим представлениям ответ на поставленный вопрос не очевиден, но он принципиально значим и поэтому актуален.

Дело в том, что в математике цифра (математический знак) ноль (0) имеет несколько смысловых значений - несколько сущностей и функций. Во-первых, ноль это обозначение абсолютного отсутствия чего-либо и его величины. Следовательно, ноль или нуль означает нисколько. В этом случае цифра ноль не есть число, так как не выражает никакую величину в количественном исчислении. На такой "пустой" ноль нельзя умножать или разделять действительные числа. При попытках сделать это числа остаются неизменными. Так, например, представляется очевидным, что любое число увеличить или уменьшить в ноль раз, то есть в нисколько раз, принципиально невозможно. По логике здравого смысла такие математические действия в реальности осуществить нельзя, поэтому умножаемое или делимое число остается неизменным. Обозначим этот абсолютный ноль обычным написанием цифры ноль, то есть как 0.

Во втором смысле за ноль в теоретической математике представляется как неопределенное, но якобы действительное число неограниченно (бесконечно) малой количественной величины, то есть как 1/?. Но это по сути дела не ноль в общепринятом понимании. Этот "ноль" обозначим полужирным написанием цифры ноль, то есть как 0. Очевидно, что 0 и 0 - это разные нули и 0 ? 0, так как 0 не есть нисколько, и по существу не является нулем. Знак 0 и не число. Он означает некоторое очень маленькое, неизвестное и неопределенное количество, приближенное к абсолютному нулю. Цифры ноль и знак бесконечность (?) не являются числами. Числа всегда выражают определенное количество чего-либо. Ноль и бесконечность, как "нисколько" и как "неопределенно большое количество чего-либо", являются понятиями о мыслимых пределах границ абсолютной шкалы положительных натуральных чисел, а их обозначения, в виде 0 и ?, не есть числа.

Практическая (прикладная) математика имеет дело только с действительными (натуральными, вещественными) числами пригодными для счета. В рамках практической математики нельзя числа делить или умножать на понятия, в частности на "нисколько" или на "неограниченно много" частей. Такие действия всегда приводят к ошибочному результату. И действительно попробуйте, например, некоторое количество (число) чего-либо практически разделить на ноль, то есть на нисколько частей. Не получится. Аналогично этому арифметически нет возможности разделить или умножить натуральное число на неизвестные значения величин, обозначаемых как - ? и + ?. Более того, не только на абсолютный ноль (0) и на ?, но и на условный (предполагаемый) ноль (0), так же как на единицу (1), никакое действительное число на самом деле (объективно, принципиально) разделить или умножить нельзя, аналогично тому как фактически невозможно ни прибавить, ни отнять ноль от нормального числа. Поэтому все рассуждения о том, что по закону Ома в "сверхпроводнике" при R = 0 или при R = 0 возникает бесконечно большой ток, не имеют истинного смысла и не подтверждаются результатами экспериментов.

Поэтому очевидно, что арифметические действия с использованием разных по смыслу нулей дают и разные результаты. Убедиться в этом не сложно.

Цифра ноль имеет ещё и третье смысловое содержание. Она, находясь среди других цифр, выражающих действительное количество некоторой величины, выполняет роль разделения других цифр в их ряду и указывает на десятикратное увеличение или уменьшение количественной характеристики выраженной набором действительных чисел от 1 до 9. Эту третью суть и функцию цифры ноль мы не рассматриваем, так как она при расчете проводимости и "сверхпроводимости" противоречиво не проявляется.

Обращаясь к формулам проводимости необходимо решить вопрос, на какой ноль (на 0 или на 0) следует разделить единицу, чтобы получить истинное значение проводимости при условии R=0 или ?=0. Иначе говоря, необходимо определиться делить ли единицу на нисколько (на 0) или же на нечто, то есть на величину 0 исчезающе малого размера равного 1/?.

Произведя формальные вычисления, получаем, что

в первом случае 0x01 graphic

и
,

а во втором варианте сомнительного расчета имеем такую количественную неопределенность:

0x01 graphic
и
.

Так как считается, что при "сверхпроводимости" электросопротивление исчезает полностью, его нет, то есть R и ? равны абсолютному нулю 0, то необходимо признать, что при этих условиях G=1 и ?=1. Это означает, что теоретически максимально возможная проводимость может быть равной 1, но не более. Естественно, что минимальное значение проводимости электричества (если она есть) всегда больше нуля. Поэтому наибольший диапазон численных значений проводимости электрического тока ограничен так:

0 < G © 1 и 0 < ? © 1 или 0 © G © 1 и 0 < ? © 1.

Существующее сейчас понятие о "сверхпроводимости" сводится к утверждению о том, что при этом явлении показатели "сверхпроводимости" являются неограниченно большими, то есть что G = ? и ? = ?. Однако это противоречит действительности, так как бесконечная (нереальная) проводимость физически невозможна с точки зрения энергопереноса по реальному проводнику электричества.

Итак, так как проводимость не может быть больше 1 (единицы), то неограниченной "сверхпроводимости" электричества, в теперешнем её понимании, не существует.

Известно, что при жизни Оннеса в теоретической части физики было довольно широко распространено негативное идеалистическое воззрение, которое могло способствовать появлению у него мнения об открытии "сверхпроводимости" электрического тока. Дело в том, что на рубеже 19-го и 20-го веков развился идеологический кризис в физике [67]. Последствия этого кризиса не преодолены до сих пор. Сущность кризиса в теоретической физике состоит в уходе ведущих ученых от адекватного материалистического описания действительности в область нереалистичных представлений, выводов и теоретических гипотез, выдаваемых за теории. В те времена было модно мыслительно и математически "открывать" невероятные крайности, например, в виде бесконечно больших масс у сверх быстро движущихся тел или у элементарных частиц, а также что элементарные частицы вещества в состоянии покоя "обладают нулевой массой". Критикуя физиков-идеалистов, В.И. Ленин в работе "Материализм и эмпириокритицизм" 1909 г. отмечал, что по их теории "материя исчезает, а остаются одни уравнения", добавим, без соответствующих граничных условий и достаточных экспериментальных подтверждений. Провозглашения нулевых и бесконечно больших значений отдельных физических параметров воспринимались как величайшие достижения физики [67].

Ученые, утверждающие существование таких безграничных крайностей как нулевые и бесконечные числовые значения свойств объектов природы, быстро становились известными, популярными и поощряемыми. Поэтому стремление теоретически "открыть" что-либо необычное, удивляющее и поражающее воображение, было характерным для физики в период деятельности Оннеса. Вероятно, это модное стремление физиков к фундаментальным открытиям в теории физических явлений повлияло на то, что Оннес поспешно, без первоначального сомнения и последующего обстоятельного обоснования и, как оказывается, ошибочно, объявил миру об обнаружении им "уникального явления сверхпроводимости" электрического тока с нулевым сопротивлением и, следовательно, с бесконечно большой проводимостью электричества металлами.

Проблема явления, названного сверхпроводимостью, была и остается актуальной в теоретическом и практическом отношениях. Возможно поэтому Г. Камерлинг-Оннес, как руководитель работ, уже в 1913 г. стал лауреатом Нобелевской премии "за сжижение гелия и обнаружение эффекта сверхпроводимости" [111], хотя его объяснение данного явления и не соответствует действительности.

Итак, при интерпретации описанных выше экспериментов Оннес ошибся, объявив, что открыл сверхпроводимость электрического тока, чем ввел в вековое по длительности и желательное заблуждение многих ученых всего мира.

Людям, особенно ученым, свойственно мечтать и верить в чудеса, в частности в то, что электрическая энергия может передаваться вдоль проводника абсолютно без сопротивления этому движению и, следовательно, без потерь проводимой по проводнику электрической энергии. Но, судя по общим законам природы, такого не может быть. И действительно, беспристрастный анализ первых же опытов со "сверхпроводниками" показывает, что, наоборот, проводники при низких закритических температурах становятся не только не сверхпроводящими, а превращаются в диэлектрики, то есть в изоляторы с идеальными диамагнитными или сверхдиамагнитными свойствами.

2.3. Эффекты, обнаруженные Оннесом
и Б. Д. Джозефсоном

В работе Я. И. Френкеля читаем: "Камерлинг-Оннесу пришло в голову разрезать сверхпроводящее свинцовое кольцо, в котором был индуцирован электрический ток, и посмотреть, что при этом получится. Казалось, что ток должен прекратиться; в действительности, однако, отклонение магнитной стрелки, регистрировавшей силу тока, при перерезке кольца нисколько не изменилось - так, как если бы кольцо представляло собой не проводник с током, а магнит" [111.С.5]. В литературе почти не упоминается "знаменитый когда-то опыт Оннеса со сверхпроводящим кольцом из свинца, в котором индуцированный ток не менялся при его рассечении" [111.С.18].

Много позднее Оннеса, в 1962 г., двадцатидвухлетний английский физик-теоретик (в то время еще аспирант по курсу экспериментальной физики в Кембриджском университете) Б. Д. Джозефсон, рассматривая свойства контакта между двумя сверхпроводниками, пришел к выводу о существовании совершенно необычных эффектов, связанных с возможностью протекания через достаточно тонкий слой диэлектрика сверхпроводящих токов. Из его теории следовало, что при нулевой разности потенциалов через диэлектрический барьер может протекать исходно постоянный сверхпроводящий ток, но чудесным образом преобразованный в высокочастотный туннельный ток. Вскоре после экспериментального обнаружения эффектов Джозефсона выяснилось, что и другие типы "слабых" контактов между двумя сверхпроводниками обладают туннельным эффектом - свободно "пропускают ток сверхпроводимости" [41]. Утверждается, что Джозефсоново туннелирование происходит при нулевой разности потенциалов электрического поля между двумя сверхпроводниками, разделенными диэлектриком, образуя сверхток:

J = J_o sin(?₁- ?₂),

где J_o - постоянная величина, а ?_1,2 - фазы некоторой волновой функции тока энергии по разные стороны от туннельного перехода (энергетического барьера) [101]. Это, по существу, есть формула тока смещения, проходящего через разделенные диэлектриком части "сверхпроводника". При этом очевидно, что электроны не перескакивают через "барьер", так как носителем в данном случае магнитной энергии является полевая материя, а не корпускулярные электроны. Поэтому в "контактах Джозефсона" нет электросопротивления. Однако, как следует из вышеприведенной формулы Джозефсона, электрический ток "сверхпроводимости" (если он там есть) все же зависит от sin(?₁-?₂), т. е. не является абсолютно неизменным, что противоречит наблюдениям и идее об идеальной проводимости.

Сейчас известно много других "туннельных контактов Джозефсона": точечные контакты двух сверхпроводников, проводник с микросужением, контакт с прослойкой из нормального металла или с прослойкой из сверхпроводника с более низким значением критической температуры T_кр.

Но что такое известный в физике твердого тела туннельный эффект? Туннельный эффект, или туннелирование, - это преодоление микрочастицей вещества потенциального барьера в случае, когда ее полная среднестатистическая энергия E меньше высоты (энергии) барьера V. Однако при E-const энергия микрочастицы, в частности электрона, не является величиной постоянной во времени и по величине равной E. Распределение энергии одной и тем более множества микрочастиц носит статистический характер, т. е. при некоторой общей (полной) энергии E часть частиц имеет энергию меньше E, а некоторая часть частиц обладает энергией E больше V (E>V), и поэтому они "преодолевают барьер" с энергией преодоления V и оказываются там, где, казалось бы, их не должно быть. Вероятность преодоления энергетического барьера тем больше, чем меньше масса частицы и чем меньше ?E = Е - V. Но всего вышеизложенного нет в "контактах Джозефсона". В них нет ?E, так как измеряемая энергия (напряженность) магнитного поля по обе стороны материальной преграды (барьера) в виде диэлектрической прослойки между "сверхпроводниками" или зазора между ними одинакова (E=V). Следовательно, в так называемых "контактах Оннеса и Джозефсона", судя по идеальной однородности (неизменности) магнитного поля до и после "контактов", можно утверждать, что в них нет энергетических барьеров, нет и туннельного эффекта. А что есть? Есть непрерывность магнитного поля исследуемого образца, имеющего различные переходы от одной его части к другой.

На основании вышеизложенного и других фактов наведения и сохранения единого магнитного поля в образцах с разделенными их частями посредством тонких диэлектрических прослоек, зазоров, сужений, микроконтактов следует вывод, что в экспериментах Оннеса и Б. Д. Джозефсона образцы вели себя подобно постоянным железным магнитам при естественных температурах. Известно, что обычный постоянный магнит, разделенный до намагничивания или после на множество частей, между которыми небольшие зазоры или немагнитные прослойки, тоже не теряет и не уменьшает свои магнитные свойства. При этом, как и в случае со "сверхпроводниками", нет туннельного эффекта (туннелирования) каких-либо микрочастиц, нет преодолений барьеров магнитным полем, так как практически нет самих барьеров в силу большой проницаемости магнитного поля.

Так как эффект неизменности магнитного поля в "сверхпроводниках" с "контактами Джозефсона" и разрезами Оннеса впервые обнаружил Оннес, а Б. Д. Джозефсон потом исследовал их, то этот эффект можно называть эффектом Оннеса-Джозефсона.

Эффект Оннеса-Джозефсона имеет принципиальное и существенное значение для достоверной теории пока что загадочного явления, обнаруженного Оннесом в 1911 г.

Проходимость электромагнитной энергии через "барьерные" контакты Онесса-Джозефсона можно объяснить установившейся в условиях закритически низких температур магнитной взаимосвязью элементов этих контактов.

В объяснении эффекта "контактов Джозефсона" с тонкими и с относительно большими диэлектрическими прослойками (изоляторами) между "сверхпроводниками", как и в случае с разрезами "сверхпроводников" Оннесом, нет ничего необычного. Исследователи таких контактов ожидали, что через слой изолятора ток протекать не может и "сверхпроводимости" быть не должно. Это так и есть. Электрический ток в таком контакте отсутствует. Однако, в экспериментах магнитомеры показывали наличие магнитного поля во всей магнитной цепи. Это объясняется тем, что диэлектрики, будучи диамагнетиками, и как считается, "сверхпроводниками" 2-го рода, первыми переходят в состояние сверхдианамагниченности, чем не затрудняют, а даже способствуют переходу в состояние "сверхпроводимости", то есть в состояние сверхдианамагниченности, соседних "сверхпроводников" 1-го рода. Однонаправленные сверхдиамагнитные поля элементов "контакта Джозефсона" обеспечивают связь всех его частей по существу сверхдиамагнитнопроводящего контакта..

2.4. Опыты В. Мейсснера и Р. Оксенфельда

В работе [41] констатируется, что в 1933 г. немецкие физики В. Мейсснер и Р. Оксенфельд обнаружили поразительный эффект, состоящий в том, что кольцевой сверхпроводник, охлажденный ниже критической температуры T_кр в постоянном во времени магнитном поле, самостоятельно переходит... в состояние "сверхпроводимости". Но это противоречит законам электродинамики, по которым в замкнутом контуре ток появляется только в том случае, если действующее на проводник магнитное поле меняется во времени. В опытах В. Мейсснера и Р. Оксенфельда магнитное поле было постоянным во времени, и поэтому не существовало причин для возникновения в кольцевом (замкнутом) проводнике ни обычной проводимости, ни "сверхпроводимости" электрического тока. Известно, что по законам электродинамики только переменное (изменяющееся) магнитное поле индуцирует (создает) в проводнике электрическое поле и этим инициирует движение электронов, которому препятствует (противодействует, сопротивляется) основное вещество проводника. Ответственными за сопротивление току электрической энергии являются возбуждающиеся при этом электроны внутри атомов проводника.

Очевидно, что материал любого проводника электричества даже при сверхнизких температурах должен оказывать определенное сопротивление движению в нем электронов. Это утверждение соответствует общему представлению о веществе, научной логике и здравому смыслу. Однако, вопреки всему Мейсснером и Оксенфельдом якобы был установлен факт возникновения в металлах даже под влиянием небольшого и постоянного магнитного поля необыкновенной "сверхпроводимости" электронов с нулевым электросопротивлением проводника при необнаруживаемом экспериментально движении в нем электронов. Но такого не может быть.

Так как "сверхпроводимость" сопровождается появлением остаточной намагниченности кольцеобразного проводника, то в данном случае приходится объяснять эффект Мейсснера-Оксенфельда созданием в проводнике метастабильной магнитной структуры материала, т. е. намагничиванием.

В. Мейсснер и Р. Оксенфельд, исследуя распределение магнитного поля вокруг сверхпроводников, установили, что напряженность магнитного поля вблизи сверхпроводника больше приложенного к нему внешнего магнитного поля. Этот факт В. Мейсснер объяснял, предположив, что внешнее магнитное поле, приложенное к проводнику до перехода его в сверхпроводящее состояние, распространяется в нем так же, как и вне его, а при переходе проводника в сверхпроводящее состояние магнитное поле вытесняется из него, усиливая магнитное поле вблизи сверхпроводника. Это спорное предположение получило широкое распространение несмотря на то, что наиболее логичным было бы объяснение увеличения напряженности магнитного поля усиленным намагничиванием проводника в условиях температур ниже T_кр.

В. Мейсснер и его сотрудник Р. Оксенфельд осуществили следующий опыт: вместо цельной проволоки из белого олова взяли оловянную трубку, поместив в ее внутренней полости маленькую катушку для измерения магнитного поля в этой полости путем поворота оси катушки. Было установлено, что при охлаждении трубки ниже T_кр магнитное поле в полости не исчезало, и, более того, это остаточное поле сохранялось в полости трубки после полного выключения внешнего поля. Это, по мнению экспериментаторов, свидетельствовало о "замораживании" магнитного поля внутри трубки. Но это проще объяснить намагничиванием проводника при температурах ниже T_кр.

Аналогичное "замораживание" магнитного поля в полости сверхпроводящего оловянного шара было установлено английскими исследователями К. Мендельсоном и И. Баббитом в 1935 г. Подобное исследование провели В. О. де Гааз и О. А. Гино. В обоих случаях наблюдалось "увеличение напряженности результирующего магнитного поля во внешнем пространстве вблизи поверхности сверхпроводника. Так, например, в экваториальной области шара при переходе последнего в сверхпроводящее состояние напряженность магнитного поля увеличилась в полтора раза" [111.С.9].

Итак, экспериментами В. Мейсснера и Р. Оксенфельда, К. Мендельсона и И. Баббита, а также других исследователей установлено:

1) при переходе материала в особое состояние при температуре ниже критической (Т_кр, К) и в результате воздействия на него электрическим, электромагнитным или магнитным полем в нем возникает магнитное поле существенно большее, чем при естественных, например, при комнатных температурах;

2) появившаяся намагниченность "замораживается", т. е. сохраняется после прекращения внешнего воздействия энергетическими полями: электрическим (постоянным током), переменным электромагнитным (индукция тока) и постоянным магнитным (непосредственное, прямое намагничивание).

2.5. К вопросу о физическом смысле

"эффекта Мейсснера"

К. Мейсснер в своих научных трудах попытался теоретически обосновать факты увеличения магнитного поля вблизи "сверхпроводника" по сравнению с напряженностью воздействующего на проводник внешнего магнитного поля, установленные им и Р. Оксенфельдом в 1933 г., а затем в опытах с шаром К. Мендельсона и И. Баббита и др. Заметим сразу же, что факт инструментального необнаружения магнитного поля внутри сплошного (не полого) "сверхпроводящего" шара не означает, что его там нет. Это вполне удовлетворительно объясняется интерференцией - явлением, возникающим при наложении двух или большего числа волн или полей в одном и том же месте. В каждой точке внутреннего объема "сверхпроводящего" шара встречаются достаточно интенсивные элементы магнитного поля, идущие от внутренней поверхности шара с разных сторон. Встречные поля компенсируют друг друга, и этим создается впечатление об их малости или отсутствии, в частности, в центральной зоне шара. Так возникает внутри шара "экранирующий эффект" от взаимодействия внешнего и наведенного диамагнитного (противоположно направленного) поля в материале шара.

Считается, что В. Мейсснером и Р. Оксенфельдом установлено, что при температуре ниже критической магнитное поле полностью выталкивается из сверхпроводника. Это предполагаемое явление называют теперь "эффектом Мейсснера". Указанное выше вытеснение или выталкивание магнитного поля (его силовых линий) из объема "сверхпроводника" проявляется, как утверждал В. Мейсснер, в увеличении напряженности результирующего магнитного поля во внешнем пространстве вблизи поверхности "сверхпроводника" [111]. Утверждение о самопроизвольном выталкивании магнитного поля из "сверхпроводника" означает, что в нем магнитная индукция В равна нулю (В=0). Если принять электросопротивление току "сверхпроводимости", как считается, тоже равным нулю (R=0), то это означает, что разность электрических потенциалов в любой точке "сверхпроводника" равна нулю (??=0) и, следовательно, вектор напряженности электрического поля Е в направлении предполагаемого сверхтока тоже равен нулю (Е=0). При условии, что индукция В=0 и электрическое поле Е=0, то какой-либо электрический ток в "сверхпроводнике" беспричинно не может течь. Поэтому ток "сверхпроводимости" I_s=0, то есть электрического тока в "сверхпроводнике" нет.

Обычно при постоянной напряженности электрического поля Е источника тока на участке проводника тока не изменяется, то есть разности напряжений ?Е и электрических потенциалов ?? идентичны то, следовательно,

0x01 graphic
,

где ?₁ и ?₂ электрические потенциалы в любых двух рассматриваемых точках проводника. При условии R=0 получаем, что ?₁=?₂, ?Е=??=0 то и I_s=0, так как нет необходимого для тока электрической энергии. Заметим кстати, что R=0 только тогда, когда на проводник не воздействует электрическое напряжение, и поэтому в нём нет электрического тока. Это очевидно. Реально ток в проводнике течет только при электрическом напряжении и при электросопротивлении R меньше некоторого критического сопротивления R_кр данного проводника, то есть если R < R_кр. При R ™ R_кр (R_кр - критическое значение электросопротивления тела полностью запирающее, непропускающее, изолирующее электрический ток) ?Е или U (U - электрическое напряжение как разность электрических потенциалов на участке любого проводника, в том числе и "сверхпроводящего", так же равны нулю и, следовательно, электрический ток I=0. Экспериментально обнаруживаемое отсутствие у "сверхпроводников" напряженности электрического поля, то есть ?Е=U=0, доказывает, что в состоянии "сверхпроводимости" ток I=0, так как для тока (направленного движения электронов) в "сверхпроводниках" нет необходимого полевого электрического потенциала - напряжения.

Утверждается, что "Мейсснер и Оксенфельд обнаружили не только отсутствие проникновения магнитного поля в сверхпроводник, но и "выталкивание" этого поля из первоначально нормального токопроводящего образца, когда он охлаждается ниже температуры Т_кр" [111.С.8], и якобы поэтому увеличивается напряженность Н вне "сверхпроводника".

Экспериментально установлено, что увеличенное внешнее магнитное поле Н разрушает "сверхпроводимость" (см. п.2.6, рис.4 и п.3.5, рис.7). Поэтому Я.И. Френкель сомневался в истинности объяснений "эффекта Мейсснера". Он задавался таким вопросом: "Если магнитное поле не может проникнуть внутрь сверхпроводника, то спрашивается, каким же образом увеличение внешнего магнитного поля может восстанавливать нормальное сопротивление тела". Тут же Я.И. Френкель так излагает ответ Мейсснера на поставленный вопрос: "Для объяснения этого обстоятельства необходимо допустить, что на самом деле внешнее магнитное поле до некоторой степени проникает в поверхностный слой сверхпроводящего тела, где при достаточной интенсивности и вызывает разрушение сверхпроводимости и восстановление нормального сопротивления" [111.С.10].

Иначе говоря, объяснение "эффекта Мейсснера" основывается на предположении что ток "сверхпроводимости" течет только в приповерхностном слое "сверхпроводника" и его диамагнитное поле блокирует и вытесняет из образца магнитное поле обычного электрического тока. В таком случае получается что, пропуская обычный электрический ток по "сверхпроводнику", в нем течет не только прежний ток, но и новый ток "сверхпроводимости" с его диамагнитным полем, направленным против магнитного поля обычного тока. Но одновременное сосуществование в "сверхпроводнике" прямого (обычного, пропускаемого) и обратного "сверхпроводящего" токов без их взаимного противодействия и, следовательно, сопротивления невозможно.

Следующее замечание. По Мейсснеру ток "сверхпроводимости" течет только в поверхностном слое провода с малым углублением ?. Однако английский физик А. Пиппард, советские физики В. Л. Гинзбург, Л. Д. Ландау и другие ученые доказывали, что в промежуточном периоде перехода металлического образца от "сверхпроводящего" состояния (S) к нормальному (N) во всем объеме материала появляется две фазы: S-фаза (область) "сверхпроводимости" и N-фаза в виде каналов нормальной проводимости. Утверждалось, что по мере перехода металла от "сверхпроводящего" состояния к нормальному состоянию S-фаза "тает", а N-области увеличиваются и, наконец, S-фаза исчезает полностью (см. об этом, например, в [41.С.36-37] и [79.С.28-30] и др.). В указанной литературе есть даже фотографии низкотемпературных S- и N-фаз промежуточного периода обратного перехода металла от "сверхпроводимости" к нормальной проводимости электричества с сопротивлением. Но нигде подробно не описывается как были получены эти фотографии. Заметим, что наблюдать и фотографировать S- и N-фазы структурных областей "сверхпроводящего" и нормального электрического тока возможно только в условиях дюара и в среде жидкого гелия при температуре меньше Т_кр. Кроме того, промежуточный период прямого и обратного переходов фазового перехода второго рода (N?S и S?N) краткосрочен, что усложняет фотосъемку структур материала в этот период. И, наконец, следующее. Фотографирование N и S фаз невозможно сделать, так как для этого надо, чтобы по образцу проходили по соответствующим каналам фаз электрические токи (обычный и "сверхпроводящий"), а фотоаппарат должен быть внутри "сверхпроводника". Однако таких возможностей непосредственного фотографирования N- и S-фаз электрического тока пока нет. Однако часто утверждается, например, то, что "размеры S- и N-областей могут быть порядка миллиметра, их можно видеть даже невооруженным глазом, покрывая поверхность образца тонким магнитным или сверхпроводящим (диамагнитным) порошком. Магнитные порошки притягиваются полем и располагаются на выходе нормальных слоев" [71.С.30]. Заметим здесь же, что нанесение порошка на поверхность образца можно сделать только вне камеры глубокого охлаждения (дюара) и при температурах на много больших Т_кр, например, при комнатной температуре, когда в образце уже не две, а одна N-фаза.

Множественное "кучкование" ферромагнитного порошка на поверхности образца прежде "сверхпроводящего" электрический ток не является свидетельством присутствия в нем N- и S-фаз электропроводности и соответствующих им S- и N-токов. Неравномерность распределения порошка на срезе теплового "сверхпроводника" логичнее объяснить наличием в образце остаточной неравномерной намагниченности материала в его объеме, так как различные домены размагничиваются после перехода S?N с разной скоростью.

Остаточная намагниченность всего объема образца в период и после S-N фазового превращения, как считается, 2-го рода доказывает, что при "сверхпроводимости" весь объем материала был в состоянии дианамагниченности и, следовательно, магнитное поле не вытесняется за пределы образца, как утверждал В. Мейсснер.

Остается пока дискуссионным вопрос, связанный с "эффектом Мейсснера", где в проволоке течет электрический ток "сверхпроводимости" - в приповерхностном слое или же во всем объеме "сверхпроводника"? Из вышеизложенного следует, что в "сверхпроводнике", при температурах менее Т_кр, тока нет, так как его сильное диамагнитное поле пронизывает весь материал, делая его диэлектриком.

Еще одно замечание к теории "эффекта Мейсснера". Некоторые современные ученые считают, что "сверхпроводник охлажденный ниже Т_кр в постоянном во времени и отличном от нуля магнитном поле, самопроизвольно "выталкивает" это поле из своего объема, переходя в состояние дианамагниченности (изолятора), и что это является результатом наложения двух полей - однородного внешнего и неоднородного внутреннего приповерхностного магнитного поля от экранизирующего тока сверхпроводимости (мейсснеровского тока), создающего внутри объема образца магнитное поле равное и противоположное внешнему" [41.С.12].

В приведенном изложении суждений автора книги [41] видно, что им осуществлена попытка совмещения ошибочного представления о вытеснении магнитного поля из "сверхпроводящего" материала с объемным принципом суперпозиции (наложения) и законом интерференции полей. Здесь уместно вспомнить, что результатом наложения (суперпозиции) однородных полей является не "вытеснение", не "выталкивание" одного другим, а их интерференция - алгебраическое сложение, приводящее к усилению или ослаблению результирующего поля в зависимости от совпадения или не совпадения направления взаимодействующих полей.

Не соглашаясь с идеей В. Мейсснера о выталкивании или вытеснении магнитного поля из "сверхпроводника", необходимо признать суперпозицию (совмещение) внешнего и "самопроизвольно" возникающего внутреннего полей и их интерференцию, которая всегда при равенстве, например, ферромагнитного (внешнего) и внутреннего антиферромагнитного (диамагнитного) полей дает нулевой результат. В связи с этим вторая часть изложенного выше суждения из книги [41] представляется логически правильной. Но далее И. М. Дмитренко, автор работы [41], вполне обоснованно написал: "Но нельзя понять причину, которая вызывает появление данной упорядоченной системы токов. Мы хорошо знаем, что в замкнутом контуре ток появляется только в том случае, когда магнитное поле меняется со временем. В случае эффекта Мейсснера поле постоянно со временем. Нет никаких причин (с точки зрения классической электродинамики) для появления токов" [41.С.12-13].

В отношении суперпозиции магнитных полей и их интерференций справедливы следующие аргументы.

1. В любом электропроводящем теле, то есть находящимся под воздействием изменяющегося потенциала электрического поля Е, есть сопутствующие электрическому току I максимально возможное магнитное поле Н и возникающее в проводнике противоположно направленное, то есть диамагнитное поле самоиндукции В. У проводников электричества

0x01 graphic
или
,

где ? = 1 + ? - магнитная проницаемость 1 < ? < 1, а

? - магнитная восприимчивость.

В силу суперпозиции и интерференции полей Н и В получается результирующее, суммарное поле Н_?. Так как В в проводнике с электричеством всегда меньше Н, то суммарное (реальное) магнитное поле Н_? проводника всегда меньше Н и оно не может при неизменном электрическом напряжении безпричинно и самопроизвольно увеличиваться. Это противоречит мейсснеровскому "выталкиванию" и "самопроизвольному увеличению" магнитного поля только вне проводника при переходе его в "сверхпроводящее" состояние.

2. В случае воздействия на тело, находящееся при температуре ниже Т_кр, только постоянным магнитным полем Н (без электрического поля Е) от внешнего источника, через вакуум или другую магнитопроводящую среду, получаем в теле то же поле Н и противоположно направленное (диамагнитное) поле -В. При определенной дианамагниченности образца, то есть когда -В=Н, напряженность суммарного магнитного поля Н_? в образце равна нулю, то есть Н_?=[Н+(-В)]=0. Это вероятно и было получено в определенных экспериментах В. Мейсснера, Р. Оксенфельда и других исследователей. Но если достигнув равенства ?-В?=?Н? продолжить воздействовать на "сверхпроводник" (при Т<Т_кр) полем Н, то в нем происходит дополнительная поляризация атомных и/или молекулярных диполей и увеличение напряженности (силы) диамагнитного поля на ?В. В итоге результирующее уже сверхдиамагнитное поле В_?=(В+?В) становится больше внешнего поля Н. Физическая природа эффекта значительного увеличения диамагнитного поля (сверхдианамагничивания) тел при температурах меньше Т_кр - низкотемпературной точки Кюри, будет подробно рассматриваться далее.

Существующие представления и теория "эффекта Мейсснера" вызывают еще много вопросов и сомнений. Рассмотрим некоторые из них.

1. Какие такие загадочные силы выталкивают из проводника внешне приложенное магнитное поле после перехода проводника в диамагнитное "сверхпроводящее" состояние? По какой причине магнитное поле, вызывающее "сверхпроводимость" электронов в "сверхпроводнике", вытесняется из него, а "сверхпроводимость" электронов остается? Если внешнее поле выталкивается появившимся собственным (внутренним) противоположно направленным полем, то оно-то уж должно быть в материале, а его, как предположил В. Мейсснер, там нет. А если внешнее и собственное поля внутри "сверхпроводника" накладываются друг на друга и взаимоуничтожаются, то почему для обеспечения эффекта Мейсснера эти поля должны быть непременно противоположно направленными, равными по величине и равномерно распределены в объеме "сверхпроводника"?

Если объяснять "мейсснеровский эффект сверхпроводников", т. е. отсутствие магнитного поля внутри "сверхпроводника" взаимоуничтожающим действием внешнего и внутринаведенного полей (а такое объяснение существует [111]), то почему это аннулирование полей одновременно и вытесняет (выталкивает) прежде проникающее в "сверпроводник" внешнее магнитное поле за пределы "сверхпроводника", усиливая тем самым магнитное поле вблизи него?

Я. И. Френкель в упомянутой выше работе [111.С.9] по поводу природы "эффекта Мейсснера" написал так: "...Находясь во внешнем магнитном поле, сверхпроводник намагничивается, но не в направлении поля, как, например, железо, а в противоположном направлении, и притом таким образом, чтобы магнитное поле, обусловленное этим намагничиванием, в точности уничтожало внешнее поле внутри сверхпроводника". Никто из ученых не объясняет, почему, собственно, намагничивание материала, будучи в "сверхпроводящем" состоянии, должно быть именно таким необычным, чтобы оправдать предположение Мейсснера о выталкивании магнитного поля из "сверхпроводника".

Соглашаясь с Я. И. Френкелем о дианамагничиваемости "сверхпроводников", утверждаем, что возникающее в "сверхпроводнике" диамагнитное поле не выталкивает внешнее магнитное поле, а, налагаясь, как бы компенсирует его, и тогда внутри "сверхпроводника" может быть, что суммарная напряженность магнитного поля равна нулю. В таком случае напряженность внешнего магнитного поля вблизи "сверхпроводника" должна не возрастать, а уменьшаться, что противоречит фактам.

2. Если магнитное поле не проникает, а выталкивается из переохлажденного "сверхпроводника", то как с его помощью в проводнике все же возбуждается, как утверждается, электрический ток "сверхпроводимости"?

3. Если внешнее магнитное поле Н не может проникнуть внутрь "сверхпроводника", а он как-то превращается из ферромагнетика или парамагнетика в идеальный диамагнетик, то каким образом увеличение внешнего магнитного поля разрушает диамагнитную "сверхпроводимость" и вновь восстанавливает нормальное состояние? С другой стороны, как абсолютный диамагнетик "замораживает" магнитное поле, если его в "сверхпроводнике" как бы и не существует из-за "эффекта Мейсснера"?

Следуя литературным источникам, "эффект Мейсснера" нужно понимать как возникновение в "сверхпроводниках" особенного диамагнетизма, который, по Мейсснеру, не является перемагничиванием, например, ферро- или парамагнитного тела в противоположном направлении по отношению к направлению приложенного внешнего магнитного поля Н, а есть какое-то необычное "выталкивание" внешнего поля из "сверхпроводника" без возникновения (без индукции) собственного магнитного поля Н_с внутри его. То есть "эффект Мейсснера" - это переход "сверхпроводника" только к внутренней немагнитности, а в вблизи его поверхности возникает и сохраняется, в отсутствии ранее приложенного магнитного поля Н, значительное магнитное поле, связанное со "сверхпроводником".

В объяснении так называемого "эффекта Мейсснера" все изрядно запутано.

Существует мнение, что исчезновение магнитного поля внутри сверхпроводника можно доказать непосредственно, вводя в толщу сверхпроводника изолированную висмутовую проволочку. Сопротивление висмута, особенно при низких температурах, возрастает с увеличением магнитного поля. Поэтому исчезновение магнитного поля в "сверхпроводнике" можно обнаружить по увеличению силы тока, проходящего через висмутовую проволочку (при постоянном напряжении). Однако известно, что изменение сопротивления (?R) висмута под влиянием магнитного поля составляет примерно 5%. Даже специальная висмутовая спираль, предназначенная для измерения силы магнитного поля, обладает невысокой точностью (~2%) и ограниченной чувствительностью. Сопротивление висмута сильно зависит от температуры. И не известно возрастание силы тока в висмутовой проволочке, находящейся внутри "сверхпроводника" при гелиевых температурах, происходит от исчезновения магнитного поля в "сверхпроводнике" или от резкого уменьшения электросопротивления в связи с глубоким ее охлаждением. По вышеуказанным причинам некоторое изменение силы тока в висмутовой проволочке, вставленной в отверстие "сверхпроводника", нельзя считать экспериментальным доказательством "эффекта Мейсснера". Это умозаключение правильно еще и потому, что "изолированная висмутовая проволочка" находится все же вне тела "сверхпроводника", а вне его, как известно и по Мейсснеру есть значительное магнитное поле.

Вывод: существование "эффекта Мейсснера" как явления выталкивания магнитного поля из "сверхпроводника" нельзя считать доказанным ни теоретически, ни экспериментально.

Допустим на минуту, что "сверхпроводник" выталкивает из себя прежде проникшее в него внешнее магнитное поле и поэтому оно становится сильнее вблизи "сверхпроводника". Однако после того как внешнее магнитное поле устранено, у "сверхпроводника" не исчезает и не уменьшается его "замороженное" поле (см., например, рис. 1, б). Это свидетельствует о намагниченности "сверхпроводника", а не о его невосприимчивости внешнего магнитного поля.

Следовательно, так называемый "эффект Мейсснера" по усилению магнитного поля вблизи "сверхпроводника" состоит не в том, что оно концентрируется вследствие непонятного вытеснения в приповерхностный слой "сверхпроводника", а наоборот, в нем создается более сильное диамагнитное поле выходящее и за его пределы. Это происходит аналогично тому, как усиленно намагничивается, например, динамная сталь при комнатных температурах.

Итак, анализ экспериментов, объясняемых "эффектом Мейсснера", приводит к выводу о том, что под действием даже частичной диаполяризации атомов вещества (дианамагничиваемости) в теле инициируется (самоиндуцируется, происходит) дополнительная диаполяризация атомов, которая усиливает дианамагничиваемость тела вплоть до полного диамагнитного насыщения, то есть до максимально возможного значения напряженности диамагнитного поля. Это сверхдианамагничивание веществ позднее будет рассмотрено подробно.

Вышеизложенное является очередным аргументом в доказательстве того, что рассматриваемое состояние веществ, называемое "сверхпроводимостью", является по существу состоянием усиленного диамагнетизма, т. е. сверхдиамагнетизма, упоминаемого в работе [24].

2.6. Диамагнитная левитация не по причине

"сверхпроводимости" электрического тока

В физике под левитацией понимают не механическое, а магнитное поднятие и зависание, т.е. парение или свободное плавание различных тел в воздушном пространстве или в вакууме. Различают эти магнитные подвесы по происхождению подъемной силы магнитных полей. Явление левитации (подвеса) вызывается разнополярностью и отталкиванием двух взаимодействующих магнитных тел. Левитация от взаимовлияния пара - и/или ферромагнитных тел хорошо известна. Очевидно, что наиболее сильное отталкивание тел происходит при взаимодействии намагниченного ферромагнетика и диамагнетика. Вероятно, первым исследователем этого взаимодействия и наиболее активно Вернер Браунбек. Он в 1939 г. теоретически рассмотрел систему, в которой одновременно действуют гравитационное, магнитное и диамагнитное поля. Он показал, что левитация возможна. Тогда же им был осуществлен свободный подвес в узкой полости вертикально расположенного электромагнита (с В - 2-3Т) графита в виде стерженьков размером около 1 см и весом до 75 мг [102.C.25]. Эксперимент был проведен и с бусинками графита [128]. Графит является диамагнетиком и намагничиваясь в противоположном направлении относительно действующего на него магнитного поля, и противодействуя ему, отталкивается, приподнимается, т. е. левитирует. Все это происходит при комнатных температурах, и ничего тут необычного нет. Однако потребовалось полвека, чтобы после Браунбека переоткрыть возможность левитации обычных, и имеющих комнатную температуру, материалов. Только в 1991 г. Э. Брюнон и Р. Тюрнье подняли в магнитном поле Биттер-магнита воду и некоторые органические материалы. Вскоре были обнаружены комнатнотемпературные диамагнитные левитации жидкого водорода и жидкого гелия, а также яиц лягушки. Теперь установлено, что левитируют в магнитном поле дерево, сыр, пицца, лягушки, мыши, кузнечики, протеин, алмаз, молекулы ДНК и многое другое [102,128]. Причем это все комнатнотемпературные диамагнитные левитации объектов.

Лауреат Нобелевской премии по физике за 2010 г. Андрей Гейм еще в 1998 г. писал, что он совместно с Жан Кинс Мааном и Петером Майном заново открыли диамагнитную левитацию. В их экспериментах левитировало практически все. Причем магнитные поля, использовавшиеся в экспериментах, уже были доступны в течение нескольких десятилетий. Требовался только час работы, чтобы получить левитацию при комнатной температуре [128].

Давно было известно, что использование идеального супер- или сверхдиамагнетизма "сверхпроводников" (т.е. использование усиленного низкотемпературного диамагнетизма "сверхпроводников") должно усиливать эффект левитации.

С целью изучения влияния низкотемпературного сверхдиамагнетизма так называемых "сверхпроводников" по просьбе В. К. Аркадьева и, по-видимому, с его участием был выполнен в 1945 г. первый эксперимент по "сверхпроводниковой" левитации. Охлаждение диамагнетиков ("сверхпроводников") производили до температур жидкого гелия. Считается, что при сверхнизких температурах диамагнетики становятся "сверхпроводниками" даже если по ним не пропускается электрический ток. В таком случае получаемую усиленную диамагнитную левитацию стали называть, без должного на то обоснования, "сверхпроводниковой".

Во вступительной статье Б. А. Введенского и Н. Н. Малова к Избранным трудам В. К. Аркадьева написано, что В. К. Аркадьев выполнил блестящий опыт с "плавающим магнитом", что "он поместил в жидкий гелий свинцовую пластинку и бросил на нее небольшой магнит. Возникшие при этом в сверхпроводящей пластинке токи были так велики, что благодаря электромагнитному взаимодействию с ними магнит после некоторых движений вверх и вниз "парил", вися над пластинкой почти неподвижно" [4.С.9]. Ни здесь, ни позднее в публикациях В. К. Аркадьева и его последователей не объясняется, как это под действием постоянного магнита в пластинке появляются сверхтоки электричества.

Сам В. К. Аркадьев в статье "О силах, действующих на диамагнитные тела" писал: "Применяя сильно диамагнитные тела, каковыми являются сверхпроводники, можно при небольшом магнитном поле иметь подвес с большой подъемной силой.

Обертывая задачу, можно заставить над сверхпроводником парить магнит.

Сверхпроводник рассматривают как тело с магнитной проницаемостью ? = 0. Ни одна линия поля магнита не входит в сверхпроводящую пластину. Это значит, что вблизи пластины линии магнитного потока магнита деформируются так, что их границей является поверхность пластинки, т. е. плоскость. Это может быть только тогда, когда в поверхности пластинки магнитное изображение магнита, в точности и во всех отношениях ему равное и симметрично с ним расположенное относительно поверхности. При этом силовой поток магнита оказывается односторонне сжатым. Вследствие этого сверхпроводящая пластинка должна действовать отталкивающим образом на всякий магнит" [4.С.301-302]. Из приведенной цитаты, очевидно, что В. К. Аркадьев признает факт левитации как результат взаимодействия магнита (магнитного поля) и его "изображения", т. е. дианамагниченной пластинки под магнитом.

Если принять, что у "сверхпроводника" магнитная проницаемость ? всегда равна нулю, то он не может дианамагничиваться под влиянием внешнего магнитного поля, а в действительности он сильно дианамагничивается. Следовательно, вначале магнитное поле проникает в "сверхпроводник", как и в комнатнотемпературные диамагнетик (при этом ? >> 0); оно вызывает (индуцирует) в "сверхпроводнике" усиленное диамагнитное поле и, как результат взаимодействия магнитного и диамагнитного полей, появляется диамагнитная левитация магнита или "сверхпроводника". После перехода "сверхпроводника" в сверхдиамагнитное состояние в него действительно не может проникнуть поле магнита и магнитная проницаемость внешнего магнитного поля в сверхдиамагнитное тело действительно может быть равна нулю.

Продолжим цитирование: "Описанные явления парения возможны благодаря тому, что магнитное поле изображения заметно не размагничивает самый магнит. Для этого он должен обладать достаточной коэрцитивной силой. Приближение к сверхпроводящей поверхности вольфрамового магнита или магнита из углеродистой стали его размагничивает настолько, что он не может преодолеть своего веса и поэтому не может парить, если его размеры не очень малы. Магниты из углеродистой стали могут парить только при размерах 0,5в9 мм и весе в несколько миллиграммов" [4.С.303].

Далее написано: "...Соображения о парении магнитов впервые доложены 12 декабря 1944 г. на конференции Московского государственного университета "Современные проблемы науки". По моей просьбе были осуществлены опыты в Институте физических проблем Академии наук в Москве в январе 1945 г. Намагниченный нифералиевый брусок квадратного сечения 4в4 мм и длиной 1 см был брошен в вогнутый свинцовый диск диаметром около 4 см, находящийся на дне сосуда Дьюара с жидким гелием. Совершив несколько упругих прыжков по вертикали, магнит после ряда сложных быстрых колебательных движений установился в горизонтальном положении над свинцом на высоте многих миллиметров. Когда, после испарения гелия, температура свинца поднялась, и он потерял сверхпроводимость, магнит спокойно лёг на диск. Приношу глубокую благодарность директору института академику П. Л. Капице за предоставление возможности осуществить этот опыт" [4.С.304].

Следуя объяснениям низкотемпературной диамагнитной левитации В. К. Аркадьева, до сих пор ошибочно считается, что "эффект Мейсснера" (? = 0) и следовательно "сверхпроводимость" доказываются экспериментом по обнаружению левитации магнита. Так, ошибочно считается, что "сверхпроводимость" и, в частности, её "эффект Мейсснера" доказываются экспериментами левитации В. К. Аркадьева [4] и других исследователей. Например, в книге Д. Шенберга [119] читаем, что "есть еще один пример демонстрации равенства нулю магнитной проницаемости сверхпроводника - это замечательный своим изяществом опыт с плавающим магнитом, сделанный Аркадьевым в 1945 г. Если маленький постоянный магнит поместить над сверхпроводящей поверхностью, то силовые линии магнита не смогут проникнуть в сверхпроводник; это создает отталкивающую силу, достаточную для преодоления веса магнита. Фотография плавающего магнита показана на рис. 3. Простейший способ понять причину отталкивания - это представить себе зеркальное изображение магнита под поверхностью сверхпроводника, которое создает в пространстве над сверхпроводником такое же поле, как и металл с нулевой магнитной проницаемостью. Отталкивание можно представить себе также как результат взаимодействия между магнитом и диамагнитным телом" [119.С.27]. Заметим, что "силовые линии магнита" никуда проникать не могут - проникает магнитное поле. Очевидно, что если магнитная проницаемость "сверхпроводника" равна нулю, то в нем, как известно, не может возникнуть ток сверхпроводимости и не может появиться, наблюдаемый в экспериментах, сверхдиамагнетизм. Последняя фраза приведенной цитаты наиболее адекватна описанию эксперимента В. К. Аркадьева с "плавающим магнитом". Анализируя опыт В. К. Аркадьева, приходим к выводу, что при гелиевой температуре магнитная проницаемость "сверхпроводника" наоборот увеличивается, но при этом изменяется её знак, т. е. изменяется направление магнитного поля внутри тела на противоположное по отношению к внешнему магнитному полю. Так возникает в переохлажденном теле метастабильное диамагнитное поле, обеспечивающее левитацию (подъем и удержание в воздухе) постоянного магнита.

0x01 graphic

Рис. 3. Плавающий магнит: освещение слева;

на правой стороне чаши видна тень магнита; белые пятнышки

на магните - кусочки затвердевшего воздуха

Итак, общее представление о физической природе эффекта "плавающего магнита" в опытах В. К. Аркадьева такова.

Если постоянный магнит с полем Н поместить вблизи или на поверхность "сверхпроводникового" материла, то силовое поле этого магнита индуцирует (порождает) в "сверхпроводнике" значительное и противоположно направленное, то есть сверхдиамагнитное поле Н_с, которое создает отталкивающую силу, большую, чем сила близкодействующего притяжения и тяжести магнита. Таким образом, постоянный магнит оказывается приподнятым и "плавающим" над "сверхпроводниковой" поверхностью, а по существу над сверхдианамагниченной поверхностью. При этом очевидно, что Н_с> Н + mg, где m - масса магнита, g - ускорение силы тяжести.

Фактически эксперимент В. К. Аркадьева состоял в следующем. Для создания устойчивого положения плавающего магнита, т. е. чтобы он не смещался в разные стороны, эксперимент проводился над поверхностью "сверхпроводящего" тела, имеющего вид полусферы или чаши. Чаша была изготовлена из немагнитного в нормальных условиях, но "сверхпроводящего", т. е. сверхдиамагнитного, при гелиевых температурах, свинца. Чашу выкрасили в белый цвет, а для наглядности формы чаши в ней нанесли черные линии. Чаша крепилась на ножках из медных прутков. Эта конструкция помещалась в жидкий гелий, уровень которого был немного ниже дна чаши. Чаша охлаждалась до температуры Т_кр, находясь в среде газообразного гелия и в непосредственной близости к диамагнитному жидкому гелию. После перехода свинцовой чаши в "сверхпроводящее" состояние, т. е. когда свинец становится способным к дианамагничиванию, в нее опускали маленький постоянный магнит прямоугольной формы, который через некоторое время, надиамагнитив чашу и, вероятно, гелий, поднимался и зависал над дном чаши на расстоянии примерно 1,5 см. На фотографии (рис. 3) приведен вид эксперимента с плавающем магнитом.

Известны подобные эксперименты с налитым в несверхпроводящую чашу жидким гелием. В этом случае жидкий гелий становится дианамагниченным и поднимает легкие намагниченные образцы.

В 1947 г. В. К. Аркадьев осуществил левитацию шара из "сверхпроводящего", читай из сверхдианамагничивающегося, материала [126]. Популярными стали опыты получения левитации магнита над "сверхпроводниками второго рода", то есть над керамическими телами (диэлектриками и изоляторами), становящимися диамагнетиками после охлаждения в диамагнитном жидком азоте.

Заметим, что в экспериментах Аркадьева, Оннеса и Джозефсона с кольцеобразным "сверхпроводником" электрический ток не использовался, однако утверждается, будто в обоих случаях там есть "сверхпроводимость электричества". Если электрический ток не подключали, то его "сверхпроводимости" не может быть. Очевидно, что физическая природа наблюдаемых Аркадьевым, Оннесом и Джозефсоном эффектов имеет не электрическую, а магнитную сущность. С другой стороны. Если задаться вопросами как в опытах Аркадьева и других, где и когда возникает ток "сверхпроводимости", откуда и куда он течёт и почему без сопротивления, то ответов нет. Следовательно, эксперименты с диамагнетной левитацией не имеют отношения к, так называемой, "сверхпроводимости" электрического тока. Физическая левитация во всех её проявлениях имеет магнитную природу. Это утверждение имеет принципиальное значение для понимания явления левитации, ее теории и последующего решения рассматриваемой нами проблемы "сверхпроводимости".

Существующее в литературе объяснение эффекта плавающего магнита В. К. Аркадьева, связанное с "неспособностью проникновения магнитного поля в "сверхпроводник", подогнано под слишком противоречивое представление об "эффекте Мейсснера".

Обратимся вновь к приведенным выше суждениям Д. Шенберга из его монографии [119]. Во-первых, "сверхпроводник" или не впускает в себя или выталкивает из себя внешнее магнитное силовое поле. В таких объяснениях большая разница. Если, по Мейсснеру, внешнее магнитное поле вытесняется из тела при появлении в нем "сверхпроводимости" электрического тока и поэтому в "сверхпроводнике" магнитного поля нет, то при непроникновении магнитного поля в "сверхпроводник" в нем поля нет, и ничего в нем не может возникнуть (так как Н=0). Не может также появиться "сверхпроводимость" с огромным магнитным противополем вне "сверхпроводника". Тут надо определиться: в "сверхпроводник" не проникает или из него проникшее внешнее магнитное поле вытесняется внутренним диамагнитным полем, индуцированным внешним (проникающим в тело) полем Н.

Во-вторых, нет сомнения в том, что до перехода к "сверхпроводимости" внешнее постоянное магнитное поле Н беспрепятственно проникает в "сверхпроводник" и возбуждает (индуцирует) в нем не электрический ток, а противоположно направленное диамагнитное поле Н_д>Н. Далее будет показано, что это обычное диамагнитное поле Н_д при переходе тела в состояние, называемое сейчас "сверхпроводящим", усиливается (самоиндукция), т. е. переходит в сверхдиамагнитное состояние с полем Н_с. В сверхдиамагнитном состоянии у тела возникает существенно большее внешнее магнитное поле, т.е. сверхдиамагнетизм. При этом происходит противодействие полей Н_с и Н, в результате которого возникают явления, подобные эффекту "плавающего" или "зависающего" тела, в частности магнита. Если убрать внешнее магнитное поле, то внутри и вне тела, находящегося в "сверхпроводящем" состоянии, остается метастабильная сверхдианамагниченность М_с с напряженностью магнитного поля Н_с (Н_с>>Н). Физическое описание природы этого явления будет еще рассмотрено достаточно подробно.

Возвращаясь к эксперименту В. К. Аркадьева с плавающим постоянным магнитом, можно утверждать, что магнитное поле магнита вызвало сверхдианамагниченность чаши и возможно низлежащего жидкого гелия, а в результате взаимодействия магнитных полей магнита и чаши с гелием магнит оказался в подвешенном состоянии. Надо признать, что "эффект Аркадьева" не доказывает, а отрицает и "эффект Мейсснера", и "сверхпроводимость" в теперешнем их понимании. Очевидно, что эксперименты Аркадьева и других доказывают магнитную природу физических левитаций как при комнатных или повышенных температурах, так и при закритически низких (отрицательных) температурах.

Диамагнитная левитация [98], при условии её значительного усиления, открывает большие возможности практического использования этого явления. Следовательно, задачей теории и прикладных исследований комнатнотемпературного сверхдиамагнетизма является получение материалов сверхдианамагничивающихся от действия относительно слабых магнитных полей, например, от магнитного поля Земли и Космоса. В таком случае вероятно можно будет создавать необычную технику, например, недорогие "диамагнитные подушки" ("диамагнитные подвесы"), а также подъемники, магнитостаты, аналогичные аэростатам, магнитолёты и др. Есть сведения, что такие работы ведутся.

2.7. Обратный переход тел от

сверхдианамагниченности к исходному состоянию

Экспериментально установлено, что чрезмерно сильное магнитное поле разрушает "сверхпроводимость", т. е. восстанавливает обычное состояние материала при условии, если напряженность этого поля Н превышает некоторое критическое значение Н_кр. Эта критическая напряженность магнитного поля тем выше, чем ниже температура, при которой находится проводник в "сверхпроводящем" (в намагниченном) состоянии. На рис. 4 показана зависимость критического магнитного поля от температуры для некоторых металлов [114].

0x01 graphic

Рис. 4. Зависимости критических сверхмагнитных полей некоторых
немагнитных "сверхпроводников" от их температуры:

1 - линия перехода свинца из сверхмагнитного состояния (S) в нормальное,
немагнитное (N)

Максимальное поле, необходимое для перевода из "сверхпроводящего" состояния в нормальное, например, олова, свинца и других металлов, происходит при температуре близкой к нулю. Это значительное магнитное поле, проходя через "сверхпроводник", воздействует на атомы, передает им некоторую дополнительную энергию, возникает межатомная коэрцитивная сила, разрушающая установившуюся ранее доменную структуру вещества, ориентированную вдоль проводника, и этим переводит, рассматриваемые в данном случае, материалы из сильно намагниченного состояния в немагнитное.

Электрофизическая теория намагничивания и размагничивания при комнатных температурах обычных ферромагнетиков, развитая Э. Х. Ленцем, Я. С. Якоби (1839 г.) и А. Г. Столетовым (1872 г.) и другими, общеизвестна (см., например, [30]), и она вполне удовлетворительно объясняет аналогичное явление, происходящее в материалах при сверхнизких температурах, когда Т<Т_кр. При температурах Т<Т_кр, вероятно, абсолютное большинство материалов (металлов и неметаллов) становится сверхмагнетиками. Это умозаключение следует из анализа множества диаграмм состояний веществ, аналогичных диаграмме, изображенной на рис. 4. Считается, что ферромагнетики, парамагнетики, диамагнетики и диэлектрики (керамика) при понижении температуры претерпевают фазовый переход второго рода и становятся сверхмагнетиками, называемыми сейчас "сверхпроводниками".

Разрушение "сверхпроводимости", т. е. сверхнамагниченности, при пропускании через проводник электрического тока значительной величины, т. е. когда ток I больше некоторого критического значения I_кр, было обнаружено раньше, чем аналогичное явление от воздействия чрезмерным магнитным полем. В случае разрушения "сверхпроводимости", а в нашем понимании сверхнамагниченности, пропусканием через такой "проводник" электрического тока I >I_кр с электрическим Е и магнитным Н полями в проводнике, происходит разрушение упорядоченной структуры магнитных диполей, т. е. их дезориентация. Это разрушает всю магнитную субмикроструктуру вещества, и оно становится размагниченным. Физическая природа этого размагничивания по существу такая же, как и при разрушении намагниченности в результате воздействия на "сверхпроводник" более сильным магнитным полем.

При исследовании магнитных свойств "сверхпроводников" определяют n - коэффициент размагничивания под влиянием магнитного или электрического поля. Коэффициент n зависит от расположения "сверхпроводника" относительно поля. В табл. 1 приведены значения n для некоторых практически важных случаев [74.С.12].

Таблица 1

Коэффициенты размагничивания "сверхпроводников"

простой формы

Форма образца	Расположение относительно Н	Коэффициент размагничивания, n
Длинный цилиндр Длинный цилиндр Тонкая пластина Тонкая пластина Шар	Вдоль поля Поперек поля Вдоль поля Поперек поля -	0 1/2 0 1 1/3

Данные табл. 1 указывают на то, что внешнее размагничивающее магнитное поле, параллельное внутреннему, не размагничивает "сверхпроводник", так как n практически равен нулю, а перпендикулярно направленное - размагничивает. Это также доказывает дипольную, магнитную природу "сверхпроводимости" исследованных образцов. Можно предположить, что несильное противоположно направленное магнитное поле способно усилить сверхдиамагнитное поле "сверхпроводника". Хорошо бы данное предположение экспериментально подтвердить или опровергнуть.

Разрушение "сверхпроводимости" происходит также и при облучении рентгеновскими лучами [15]. Вероятно, что разрушение "сверхпроводимости" будет происходить и при воздействии ультразвуком определенной частоты.

Итак, "сверхпроводимость" электрического тока исчезает, если на материал в "сверхпроводящем" состоянии воздействовать сильным магнитным полем или пропускать по нему большой постоянный или переменный электрический ток, а также при облучении рентгеновскими лучами и при повышении температуры "сверхпроводника". Исчезновение "сверхпроводимости" под влиянием вышеперечисленных внешних факторов свидетельствует о том, что мы имеем дело не со "сверхпроводимостью" электрического тока, а с супернамагничиваемостью, т. е. со сверхнамагничиваемостью материалов при закритически низких температурах.

2.8. Новый подход к развитию полевой

теории электрического тока и намагничиваемости тел

Знаем, что сущности любых объектов природы (предметов и явлений) таковы, что в них обязательно есть противоположные и противодействующие свойства, соотношения которых в определенных условиях характеризует и предопределяет процессы изменений, движений и направление развития объекта. Комплексное рассмотрение всех противоположных свойств объекта в их единстве, взаимосвязи и борьбе (противодействии), с учетом количественно-качественных закономерностей и обратимых переходов из одного качественного состояния объекта в другое, есть диалектический подход (метод) его исследования. В явлении "сверхпроводимости" есть хорошо известные противоположные свойства, постоянно проявляющиеся на практике. Эти противоположные пары свойств (например, электрические и диэлектрические, магнитные и диамагнитные и др.) органически взаимосвязаны и находятся в обратной зависимости друг от друга, что свидетельствует об их "борьбе" в философском и в прямом смыслах этого слова. В данном параграфе изложена попытка обобщенного диалектико-материалистического описания электромагнитных свойств тел с выходом их на другой уровень качества - на переход к сверхдиамагнетизму и в абсолютно диэлектрическое состояние при низких температурах, меньших критического значения для каждого конкретного вещества.

Известно, что М.Фарадей еще в 1831 г. "изучая природу электрического действия" экспериментально обнаружил у различных материалов одновременное существование противоположных электрических и магнитных свойств. Так, например, в отношении электрического тока он написал: "... Оказывается, что обычные явления изоляции и проводимости друг с другом тесно связаны, или, вернее, представляют собой предельные случаи одного и того же состояния" [103.С.552]. Изоляция или диэлектризация, по Фарадею "означает индукцию", т.е. противоположное действие, сопротивление электрическому току от индуцированных током диэлектрического и диамагнитного полей.

Впоследствии Максвелл рассматривал раздельно индукцию диэлектрического D и диамагнитного B полей в теле с постоянным током и его неизменяющимися полями E и H от источника постоянного тока (батареи). Для указанных полей индукции Максвелл написал следующие общеизвестные формулы:

D = ?E и B = ?H,

где ? - диэлектрическая проницаемость; ? - магнитная (правильнее назвать диамагнитная) проницаемость.

Признавая у тел диэлектрическую проницаемость, т.е. проницаемость противополя D, необходимо ввести понятие и обозначение прямой электрической проницаемости поля E в тело, тем более что электрическая проницаемость проявляется не менее явно, чем диэлектрическая проницаемость. Точно так же, если в макроскопической теории о магнетизме есть магнитная проницаемость, а в токопроводящем теле есть магнитное и индуцированное диамагнитное поле, то должна быть характеристика и диамагнитной проницаемости. В соответствии с этим и, следуя логике Максвелла, считаем, что если электрическое поле E воздействует на тело, то в нём возникает (индуцируется) два поля: положительное электрическое Е_п и отрицательное диэлектрическое D_п. В таком случае получаем, что

Е_п = ?_ЭЕ,

- D_п = ?_ДE,

где Е_п и D_п - удельные электрическое и диэлектрическое поля проводника; ?_Эи ?_Д - электрическая и диэлектрическая проницаемости соответственно; Е - электрическое поле источника электрической энергии, т.е. внешнее воздействующее на проводник электрическое поле.

В ряде работ, в частности в [66.С.73-74] количественная зависимость вектора диэлектрической индукции D_п ("электрического смещения") определяется выражением:

D_п = ?_оE + P,

где E - напряженность электрического поля,

Р - вектор электрической поляризованности вещества,

?_о - электрическая постоянная равная - 0,885?10^-11 Ф/м.

Считается, что векторы Р и Е связаны следующим соотношением:

Р = ?_о?Е,

где ? - некоторый безразмерный коэффициент пропорциональности, названный показателем диэлектрической восприимчивости.

Отсюда следует, что

D_п = ?_оE + ?_о?Е = ?_о(1 + ?)Е.

Выражение 1 + ?, где присутствует показатель восприимчивости ?, почему-то часто называют диэлектрической проницаемостью, и считают, что

? = 1 + ?.

Поэтому пишут, что D_п = ?_о?Е и, следовательно, Е зависит только от величины диэлектрической проницаемости ?.

Здесь наблюдается явное смешение разных по содержанию понятий, следовательно, приведенные выше три формулы должны быть уточнены.

Вероятно, что электрическая проницаемость проводника с током ?_э = 1 - ?_д, а сумма их абсолютных величин | ?_э + ( - ?_д)| = 1. Поэтому 0 < ?_э < 1 так же как и 0 < ?_д < 1. При ?_э - 1 - идеальный проводник, а при ?_д - 1 - идеальный диэлектрик (абсолютный изолятор).

Общее электрическое поле Е_п проводника с электрическим током можно записать так:

Е ? Е_п= ?_эЕ - ?_дЕ,

здесь и далее знак ? означает "влечет за собой" (например, приложенное поле Е влечет за собой появление в теле поля Е_п).

При ?_э = ?_д проводник становится слабым диэлектриком.

Так как "всякий электрический ток сопровождается магнитным действием соответствующей интенсивности" [103.С.12], то в проводнике с током индуцируются два противоположно действующих силовых поля: положительное ферромагнитное или парамагнитное и отрицательное диамагнитное или сверхдиамагнитное. Для этих полей, в развитие и дополнение максвелловской общей формулы В = ?Н, можно записать зависимости магнитного поля внутри проводника с током Н_и и диамагнитного поля В_д от магнитного поля, создаваемого источником электрического тока Н_и, так:

Н_м = ?_мН_и,

В_д = ?_дН_и,

где Н_м и В_д - магнитное и диамагнитное поля в проводнике с электрическим током,

?_м и ?_д - магнитная и диамагнитная проницаемости,

Н_и- магнитное поле проводника, создаваемое источником тока электрической энергии.

Если не учитывать магнитную восприимчивость материалов, что часто делается, а считать намагничиваемость проводника с током зависящей исключительно от магнитной проницаемости, то общее магнитное поле проводника Н_п с электрическим током запишется как геометрическая разница значений Н_м и В_д:

Н_п = |Н_м - В_д|,

где, если В_д < Н_м, то магнитное поле проводника равно

Н_п = Н_м - В_д, но если численное значение В_д (при понижении температуры проводника) становится больше или Н_м - Н_и = Н, то проводник становится диамагнетиком и диэлектриком (изолятором) с диамагнитным полем этого тела равным:

В_т = - (В_д - Н_м).

Эти формулы показывают только то, что в любом проводнике с электрическим током индуцируется два взаимопротивоположных магнитных поля Н_м и В_д. Их количественные соотношения предопределяют магнетизм и проводимость электричества или диамагнетизм и диэлектричность (изоляционную способность) материала.

В случае воздействия на тело только внешним магнитным полем Н, то в теле возникают два поля: Н_м - внутреннее магнитное поле и встречное, противоположно направленное, то есть диамагнитное поле В_д. Поэтому, как и в случае с магнитным полем от электрического тока, в теле создается результирующее внутреннее магнитное поле тела Н_т, состоящее из собственного магнитного поля Н_м - H и индуцированного диамагнитного поля В_д. При этом, по аналогии с известной общей формулой В = ?Н можно точнее записать, что

Н_м = ?_мН и В_д = -?_дН.

Следовательно, обычно

Н_т= Н_м - В_д,

где Н_т- итоговое (обобщенное) магнитное поле тела, находящегося во внешнем магнитном поле Н (обычно Н_т < Н).

У ферромагнетиков и парамагнетиков характеристики проницаемости электрического и магнитного полей имеют знак плюс. Показатели (коэффициенты) проницаемости индукции полей ?_д и ?_д имеют отрицательный знак. Эти знаки указывают направление индуцированного поля по отношению к внешнему воздействию.

Опыт показывал, что численные значения проницаемостей полей в данное тело практически не зависят от направления действия этих полей. Отсюда следует, что для крайних случаев показатели (коэффициенты) электрической и магнитной проницаемостей при умеренных температурах одинаковы (изотропический эффект) и близки к единице. Аналогичное суждение распространяется и на проницаемости отдельно рассматриваемых магнитного и диамагнитного полей в конкретном теле. Однако, при одновременном взаимовлиянии рассматриваемых полей (при их наложении) значения проницаемостей должны быть разными.

Вполне очевидно, что у любого тела есть противоположные (противоборствующие) свойства и соответствующие характеристики как электрической, так и диэлектрической проницаемости, а также есть коэффициенты магнитной и диамагнитной проницаемости. В теории суммы взаимосвязанных коэффициентов ?_э и ?_д, а также ?_м и ?_д всегда должны быть равными единице.

Если ?_э немного больше ?_д, то это относительно слабый проводник электрического поля и, следовательно, электрического тока; при ?_э >> ?_д - хороший проводник; при ?_э - ?_д - неустойчивое состояние (полупроводник); при ?_э < ?_д - стабильный диэлектрик (изолятор), а при ?_э << ?_д - абсолютный диэлектрик (абсолютный изолятор).

Если ?_м не на много больше ?_д, то это означает малую намагничиваемость объемного тела (возможно, намагничивается не весь его объем); при ?_м >>?_д - возможность намагничиваемости большого тела; при ?_м- ?_д сумма ?_м + ?_д - 0 тело находится в нестабильном состоянии в отношении намагничиваемости; при ?_мд и при ?_м << ?_д - материал тела становится устойчивым диамагнетиком. Численные значения проницаемостей материалов ?_э, ?_д, ?_м и ?_д зависят от многих факторов: от величин Е и Н, от температуры, механического напряжения, проникающего облучения и других внешних условий для данного тела.

Напряженность магнитного поля тела зависит не только от магнитной проницаемости, но и от магнитной восприимчивости материала ? и от его массы m.

"Опыт дает, что для диа- и парамагнетиков намагниченность пропорциональна напряженности поля:

Н_т = М = ?Н.

... Для парамагнетиков величина ? положительна, для диамагнетиков - отрицательна" [70.С.423]. Следует уточнить, что здесь и далее слово "отрицательное" означает, не то, что арифметически ? < 0, а то, что этот коэффициент со знаком "минус" указывает на противоположную направленность, образующегося в теле диамагнитного поля по отношению к внешнему для тела полю H. Количественно ? всегда больше нуля, так как абсолютных значений натуральных чисел объективно меньше нуля, то есть меньше чем нисколько, не бывает. Численное значение ? у магнетиков и диэлектриков существенно разнятся. Это учитывается при определении намагничиваемости разных материалов.

Представляется, что известную формулу ? = 1 + ? , показывающую связь проницаемости и восприимчивости намагничивания тел [47.С.294 и др.], нельзя считать абсолютно правильной, так как в ней сопоставлены разные по физической природе характеристики. Хорошо, что в физике есть понятия диэлектрической и диамагнитной восприимчивости. Но пока не определена их взаимозависимость, взаимообусловленность. Численные соотношения названных восприимчивостей и соответствующих проницаемостей совместно предопределяют величины электрических и магнитных свойств материалов. Так, например, характеристики диамагнитного и магнитного полей, а также диэлектрического и электрического полей в магнетике имеют обратные зависимости: чем больше В, тем меньше Н_т; чем больше D, тем меньше

Е_т = Е_э - D. В этом проявляются сопротивления магнитному потоку и распространению (току) электрического поля.

С другой стороны, если магнитная восприимчивость ?_м больше диамагнитной ?_д и магнитная проницаемость ?_м больше диамагнитной проницаемости ?_д, то материал является магнетиком (ферро- или парамагнетиком) и проводником электричества. Если ?_м= ?_д, то есть когда ?_м+ (- ?_д) = 0 и ?_м= ?_д, то материал не обладает магнетизмом, то есть является слабым и неустойчивым диамагнетиком и слабым диэлектриком (полупроводником?). Если же ?_д > ?_м, то это относительно стабильный диамагнетик. При ?_д >> ?_м - сверхдиамагнетик. Относительно "сверхпроводников" достоверно утверждение о том, что "поведение сверхпроводника в магнитном поле схоже с поведением идеального диамагнетика" [74.С.10] и оно "соответствует представлению о сверхдиамагнитном теле" [111.С.11]. Очевидно, что идеальный диамагнетик или сверхдиамагнетик это одновременно и сильный диэлектрик (абсолютный диэлектрик, хороший изолятор).

Суждения о магнитных свойствах, аналогичные вышеизложенным, будут справедливы и для соотношений электрических полей и электрического тока в различных телах.

Итак, в макроскопической теории электрического тока, электрических и магнитных полей необходимо учитывать единство и противодействие противоположных свойств реальных тел. При таком диалектическом подходе появляется возможность выяснить физическую природу (сущность, содержание) рассматриваемых явлений: проницаемости электрического и магнитного полей, проводимости и электросопротивления току электрической энергии, "сверхпроводимости" и изоляции, а также магнитных и диамагнитных свойств, включая сверхдианамагничиваемость веществ.

При решении проблемы "сверхпроводимости электрического тока", а, по существу, проблемы сверхдиамагнетизма, требуется не только адекватное макроскопическое описание проявлений электрических и магнитных свойств, но и модельное представление о микроскопических процессах происходящих внутри тела при макроскопическом проявлении его свойств, в частности, магнетизма или диамагнетизма, проводимости или непроводимости (изоляции) электрического тока. Поэтому вопрос о микроскопическом представлении и научнообоснованном описании ферро- и парамагнетизма, диамагнетизма и сверхдиамагнетизма и других свойств с позиций строения веществ и их атомов имеет принципиальное и весьма существенное значение.

Известно, что диамагнетизм - один из видов магнетизма, проявляющийся в намагничивании вещества навстречу направлению действующего на него внешнего магнитного поля любого другого вида (ферромагнитного или парамагнитного). Диамагнетизм присущ всем веществам, но проявление его часто затруднено из-за преобладания обычного магнетизма, совпадающего по направлению поля с направлением действия внешнего намагничивающего поля. Ферромагнетики и парамагнетики в своей электронной структуре атомов имеют готовые магнитные диполи с N и S полюсами. В таком случае внешнее магнитное поле Н, не изменяя орбитальные движения дипольных пар электронов, легко разворачивают диполи так, чтобы их магнитные моменты P_mi совпадали с направлением действия внешнего магнитного поля. Так, по существу, происходит ферро- или паранамагничивание.

У немагнитных веществ в их электронной структуре атомов нет естественных магнитных диполей и поэтому их намагничивание сильно затруднено, так как спаренные электроны атомов не обладают магнитным моментом. Это обусловлено тем, что электроны атомов, попарно взаимодействуя и вращаясь по удаленным от своих ядер круговым стационарным орбитам, имеют противоположные спины. При этих условиях магнитные моменты спаренных атомов, складываясь, компенсируют друг друга. Из таких магнитонейтральных атомов и молекул состоят немагнитные вещества при соответствующих для этого температурных условиях.

Примером простейшего и слабого диамагнетика является нейтральный гелий. Атом гелия имеет два взаимоотталкивающихся электрона с противоположными спинами и вращающихся по устойчивым круговым, внецентровым, по отношению к ядру атома, и равноудаленным от ядра орбитам. При этом орбитальные магнитные моменты парных электронов равны по величине, но противоположны по знаку, и поэтому суммарный магнитный момент P_m атома равен нулю. Такая модель атома гелия приведена в работе [124, разд. "Диамагнетизм". С.304-306, рис.6.3], и она вполне согласуется с предлагаемой микроскопической моделью электронного строения атомов (см. разд. 3).

Принято считать, что спины электронов оцениваются, как Ђ Ґ, то есть электрон имеет спин + Ґ или - Ґ. Исходя из того, что в атоме электроны взаимодействуют попарно, и если оба электрона имеют спины + Ґ, то их общий спин равен + 1. Это означает, что образованный парой электронов магнитный диполь, имея характеристику + 1, является пара- или ферромагнитным. В случае, когда оба электрона вращаются вокруг собственной оси в другую сторону, то их спины равны - Ґ, то суммарно эта пара электронов образует магнитный диполь с характеристикой - 1, что означает диамагнетизм данного диполя. Когда в атоме внешние "спаренные" электроны имеют разные спины, то есть если один электрон имеет спин - Ґ, а другой + Ґ, то в сумме их общее магнитное поле равно нулю. В таком случае атом в магнитном отношении нейтрален: он при естественных температурах не намагничивается и не реагирует на внешнее магнитное поле.

Количество магнитных или диамагнитных атомных диполей в теле определяет степень его намагничиваемости или дианамагничиваемости. Если в сложном по химическому составу теле количество магнитных и диамагнитных диполей равно или все атомы в магнитном отношении нейтральны, то тело немагнитно. Под влиянием внешнего магнитного поля и при благоприятных (низких) температурах спины электронов могут изменяться. При этом магнетик может становиться диамагнетиком, немагнетик может превращаться в магнетик или в диамагнетик с разной степенью намагничиваемости (поляризуемости диполей). Процесс магнитного превращения тел из любого состояния в сверхдиамагнитное следует называть фазовым превращением третьего рода.

По степени (силе) и виду намагничиваемости тела можно классифицировать так: ферромагнетик это сверхпарамагнетик, а сверхдиамагнетик это более сильный низкотемпературный диамагнетик. Эксперименты показали, что сверхдиамагнетик в 2 и более раза сильнее намагничивается, чем комнатнотемпературный ферромагнетик.

При внесении вещества в магнитное поле H на движущиеся по круговым орбитам электроны действует магнитная индукция B_o, которая создает свой дополнительный магнитный момент электрону ?P. Этот наведенный магнитный момент ?P всегда, по закону Ленца, противоположен внешнему магнитному полю Н (Н=В). При условии ?P>P электрон меняет направление своего движения так, что направления действия ?P и P совпадают, но при этом В_д становится направленным против внешнего намагничивающего поля Н. В результате этого процесса сопряженная пара электронов становится диамагнитным диполем, а его суммарный магнитный момент равен P= 2(P_m+?P_m). Учитывая, что при ?P>P большинство атомов тела становятся дианамагниченными, то суммарное диамагнитное поле В_д оказывается намного больше внешнего намагничивающего поля H (В_д>>Н), а это и есть сверхдиамагнетизм. Схема намагниченного, диаполяризованного (с диамагнитным диполем) атома гелия показана далее (п. 4.3, рис. 24).

При нормальных (близких к комнатным) температурах магнитная восприимчивость (намагничиваемость) одного моля парамагнитного, ферромагнитного и диамагнитного веществ ? мала и составляет от 10^-8 до 10^-3. Однако среднее значение ?-10^-6. Так, например, у одного моля гелия ? = 1,9·10^-6. Но намного большие значения диамагнитной восприимчивости имеют вещества ("сверхдиамагнетики") при закритических, экстремально низких температурах. В этих условиях практически любое вещество становится диамагнетиком с диамагнитной восприимчивостью, равной в среднем ? = -8 · 10^-1= -0,8. Такое близкое к 1,0 значение ? почти идеальной магнитной восприимчивости вещества предопределяет сверхбольшое значение напряженности диамагнитного поля В_д, т. е. их сверхдианамагничиваемость. Так вещества становятся сверхдиамагнетиками.

Приведенное здесь краткое описание природы сверхдиамагнетизма вполне согласуется с предлагаемой автором моделью электронного строения атомов и с обоснованием перехода веществ в сверхдианамагниченное состояние при криогенных температурах в результате воздействия на твердые тела постоянным магнитным полем электрического тока или внешним постоянным магнитным полем.

Далее переход веществ в сверхдиамагнитное состояние будет рассмотрен более подробно.

3. КРАТКИЙ АНАЛИЗ ОСНОВНЫХ ТЕОРИЙ "СВЕРХПРОВОДИМОСТИ" ЭЛЕКТРИЧЕСКОГО ТОКА

3.1. Понятия об электрических зарядах,

электрическом токе и электросопротивлении

проводников

Думается, что проблема "сверхпроводимости", т. е. проблема создания адекватной теории этого физического явления и материалов с умеренной (близкой к комнатной) температурой перехода в это состояние не может быть решенной без нового осмысления, что такое электричество, электрические заряды, электрическое и магнитные поля, электрический ток в проводнике и т. п. Кратко рассмотрим эти понятия.

История электричества началась более чем 2000 лет тому назад, когда было обнаружено, что если потереть шерстью янтарь, то он приобретает свойство притягивать к себе легкие предметы (перья, нити и т. п.). Это свойство назвали электричеством (от греческого слова elektron - янтарь), т. е. свойством янтаря. Позднее обнаружили, что электричество стеклянной палочки, натертой кожей, действует противоположно электричеству янтаря. Практические действия по электризации янтарной и стеклянной палочек названы заряжением. Слово "зарядить" означает повторяющиеся одинаковые действия. Поэтому натирание электризующих палочек для наведения в них электричества было названо заряжением, а величина заряженного, приобретенного электричества - электрическим зарядом. Электрический заряд стеклянной палочки получил условное название "положительный", а заряд смолы (янтаря), которую потерли мехом, назвали "отрицательным". Вскоре же было установлено, что предметы с одноименными зарядами отталкиваются друг от друга; с разноименными зарядами - притягиваются друг к другу, а при соединении двух предметов с разными зарядами, но одинаковыми по величине - нейтрализуются.

Для того чтобы количественно определять величину заряда, введено понятие единичного, или точечного, заряда. Точечным зарядом q называется наэлектризованное тело, размеры которого предельно малы по сравнению с расстоянием до другого заряженного тела, с которым оно взаимодействует.

Факт, что электрические заряды взаимодействуют между собой. Вопрос: что является носителем (объектом), осуществляющим взаимодействия электрических зарядов? Ответ: электрические поля наэлектризованных тел. Следовательно, заряды - это сами взаимодействующие электрические поля тел и их частиц.

Зная, что разные электрические заряды и, следовательно, их электрические поля бывают положительными (отталкивающими) и отрицательными (притягивающими, к себе противоположно заряженные и незаряженные тела), т. е., понимая, что электрические заряды и электрические поля являются одновременно и магнитными, так как они притягивают или отталкивают другие тела, можно с уверенностью утверждать, что электрическое и магнитное поля - это две составляющие, два вектора состояния или движения единого электромагнитного поля. Но что такое электромагнитное поле вокруг заряженных тел? Это движущаяся невещественная (бесструктурная) материя [105], называемая материальным вакуумом, полевой материей или эфиром. Движение вещественной (структурной) материи (вещества) приводит в движение полевую материю (материю вакуума), и, наоборот, движение материи, называемой вакуумной, или полевой, вызывает движение электрических частиц, атомов, молекул веществ, малых и больших тел.

В вопросе о зарядах давно существуют правильные догадки о том, что в телах есть домены, диполи, молекулярные и атомные магнитики, поляризация и т. д.

Диполь - совокупность двух равных по величине разноименных точечных (единичных) электрических зарядов, находящихся на некотором расстоянии друг от друга.

Домен - отдельные микроскопические области тела, намагниченные до насыщения. Под влиянием внешнего воздействия диполи в доменах ориентируются в объеме тела по направлению электрической (Е) или магнитной (Н) составляющей единого поля. Названные магнитики (домены, диполи), параллельно выстроенные в теле, намагничивают его, и такое тело становится ферромагнетиком, парамагнетиком или диамагнетиком.

Если атомная или молекулярная микроструктура тела позволяет внутриатомным диполям разворачиваться в направлении приложенного поля, но если после прекращения воздействия полем диполи не удерживаются в этом направлении, то такое тело размагничивается. В случае если микромагнитики не имеют возможности ориентироваться в направлении действующего поля, т. е. они не могут составлять цепочки диполей (доменов), то, следовательно, они не способны воспринимать и передавать энергию приложенного поля. Такие тела являются диэлектриками (изоляторами) и немагнетиками.

Очевидно, что каждый диполь в теле обладает своим замкнутым электромагнитным полем. А множество однонаправленных диполей создают общее (коллективное) поле, уже жестко не связанное с отдельными диполями (зарядами). Это обобщенное поле, относительно свободное от диполей (спаренных единичных зарядов), будучи движением вакуумной материи вне заряженных частиц вещества, влияет на соседние, хаотически расположенные диполи, разворачивает их в своем направлении и таким образом, перемещаясь, распространяется по телу проводника. Следовательно, носителем электрической энергии являются не заряды или диполи токопроводящего тела, а их обобщенное энергетическое поле вакуумной материи проводника. Работа, затрачиваемая на поляризацию диполей в проводнике, есть основная часть его электросопротивления электрическому току. Кстати, становится объяснимым, почему общее поле может отрываться от своего проводника (от радиоантенны, от антенны локатора, от телепередающей антенны, от сварочного электрода и т. д.) и распространяться не только вдоль проводника, но и в свободном пространстве вплоть до космического. Волновой характер радиоизлучения подтверждает, что носителем излучаемой энергии является общее поле источника этого излучения (проводника), а не какие-либо его вещественные частицы, например, электроны. Так в общих чертах представляется автору процесс распространения тока электрической энергии по проводнику и вне его.

В настоящее время считается, что электрический ток - это направленное движение электрических зарядов. Примером такого тока является перенос электрической энергии заряженными телами и частицами. Такой ток происходит, в частности, в жидком аккумуляторе, и он называется конвекционным (переносным).

Считается, что и в проводнике под воздействием внешнего электрического поля Е свободные электрические заряды двигаются так: положительные - по полю, а отрицательные - против действующего поля. Случай, когда микроскопические электрические заряды движутся внутри неподвижного макроскопического тела (твердого, жидкого или газообразного), носит название тока проводимости.

Третьей разновидностью тока проводимости считается ток в вакууме, когда микроскопические электрические заряды движутся в пустоте, независимо от их телесных источников [47]. В качестве примера тока в вакууме приводят потоки электронов в электронной лампе, что не корректно. Вполне возможно, что здесь все наоборот: эмиссия и движение электронов происходят не независимо от макроскопических тел (катода и анода), а в результате разогрева катода и влияния электрического поля Е, т. е. потока энергии от катода к аноду.

Если действительно "электрический ток - это поток свободных электронов, несущих заряды через кристаллическую решетку металла" [72. С. 328], то для потока электронов в металле принципиально важным показателем является скорость распространения тока, или скорость движения "свободных" электронов. Известно, что скорость распространения электричества вдоль проводника очень большая. Например, если включить электрический ток, например, в Красноярске, то через мгновение в Санкт-Петербурге загорится электролампочка от "пришедшего по проводам" электрического тока. Но не может такого быть, чтобы "красноярские" электроны так быстро преодолели расстояние в тысячи километров.

Считается, что скорость электронов в постоянном токе определяется из уравнения плотности тока проводимости в металлах

0x01 graphic
,

где n - число электронов проводимости в единице объема (концентрация носителей тока), е - абсолютное значение заряда электрона,

- вектор средней скорости упорядоченного движения электронов. В металлах n и е являются постоянными величинами, а модуль вектора

имеет значения порядка 10^-4 м/с при максимальных значениях плотностей токов. Например, в медном проводнике n - 8,5?10²⁵ м^-3, наибольшая плотность тока J = 1,1?10⁷ А/см², тогда ? - 8?10^-4 м/с - 0,8 мм/с [124.С.233]. С такой скоростью электроны проводимости большие расстояния и быстро преодолеть не могут. Следовательно, передает энергию по проводам "тонкая, бесструктурная материя", т. е. материя вакуума, называвшаяся когда-то эфиром.

По имеющимся оценкам, скорость распространения электрического тока равна скорости света. Скорость света - это константа, характерная для движений "тонкой и бесструктурной" материи вакуума. Из этого следует, что ток электрической энергии не есть движение электронов, что переносчиком электричества является напряженное электромагнитное поле, распространяющееся не внутри, а в основном вне проводника, то есть в вакууме (в эфире) [76].

По поводу полевой электромагнитной, а не электронной природы электрического тока есть множество суждений ученых. Например, в случае переменного тока проводимости "под электрической энергией понимают энергию электромагнитного поля", а не движущихся электронов; или еще: "нестатические, переменные электрические поля могут существовать совместно с переменными магнитными полями в отрыве от электрических зарядов" [47.С.15].

Очевидно, что электромагнитная природа электрического тока носит волновой, а не корпускулярный характер. Корпускулярные электроны при пропускании электрического тока вдоль проводника остаются на своих местах - в структуре атомов. Предположение о существовании в металлах и других проводниках "свободных" электронов ничем не обосновано и противоречит фактам. Отрыв электронов от атомов и их локальные (например, тепловые) движения происходят только вследствие чрезмерного тока, разогрева проводника и действия электрических или магнитных сил.

Для понимания "сверхпроводимости" нас весьма интересует механизм (физическая природа) передачи электрической энергии (электричества, т. е. электрического тока) в обычном проводнике. По данному вопросу, как обычно, читаем: "Электрический проводник - вещество, основным свойством которого является электропроводность. В металлах и сплавах протекание электрического тока является следствием направленного движения носителей заряда - свободных электронов, не связанных жестко с кристаллической решеткой металла. Различная проводимость различных металлов и сплавов обусловлена разным числом в них свободных электронов на единицу объема, а также их подвижностью" [9.С.565]. Под электрическим сопротивлением понимается противодействие, которое оказывает проводник движущимся в нем электрическим зарядам, в частности, свободным электронам. Считается, что электросопротивление при нормальных температурах обусловлено тепловым движением атомов проводника. При возрастании температуры повышаются тепловые колебания атомов проводника и увеличиваются столкновения электронов (носителей зарядов) с атомами, что препятствует движению электронов и этим повышает сопротивление электрическому току. Снижение температуры, наоборот, уменьшает амплитуду колебаний атомов и, следовательно, уменьшает количество столкновений электронов с атомами, потери энергии электронов уменьшаются, сопротивление проводника движению в нем электронов уменьшается.

Прежде предполагалось, что при абсолютном нуле температуры атомная структура вещества неподвижна, и если размеры атомов становятся ничтожно малыми, то электросопротивление такого идеального проводника должно быть равным нулю (рис. 5, кривая 1). Исходя из этих предположений и опытов по "сверхпроводимости", был сделан ошибочный вывод: "сверхпроводящие" материалы являются идеальными проводниками. Позднее под давлением фактов этот вывод-предположение был опровергнут, да он и изначально-то был неправдоподобным, так как движущиеся электроны не могут абсолютно не взаимодействовать с атомами, а увеличивающаяся при охлаждении плотность атомов (и без того плотноупакованной кристаллической решетки, например, металлического проводника) должна увеличивать электросопротивление (рис. 5, кривая 3).

Так как любой проводник не идеален, то электроны непременно сталкиваются с атомами проводника даже при абсолютно нулевой температуре, поэтому электросопротивление не может быть меньше некоторого минимального значения, что было подтверждено еще Оннесом при исследовании электрических свойств платины при сверхнизких температурах. Этот факт схематично показан на рис. 5, кривая 2.

Известно, что у некоторых металлов наблюдалось увеличение электросопротивления при очень низких температурах. Это объясняется предполагаемой конденсацией свободных электронов на атомы, вследствие чего проводимость (количество проводимого электричества), определяемая числом свободных электронов в теле, уменьшается (рис. 5, кривая 3), а так как при температуре 0 К все свободные электроны закрепляются в атомах, то электросопротивление должно стремиться к бесконечности (R??), а не к нулю (R=0) [9] и [119].

В работе [9] правильно указывается, что "приведенные точки зрения не могут объяснить, почему при некотором значении температуры (ниже T_кр. - В. Ф.) между электронами и решеткой внезапно прекращаются соударения - обмен энергией, т. е. возникает сверхпроводимость" [9.С.329].

0x01 graphic

Рис. 5. Зависимость электросопротивления проводников
от температуры

На основе вышеизложенного надо привести нижеследующее ключевые суждения, необходимые для соответствующего понимания физики электрических зарядов, электрического и магнитного полей, электрического тока и электросопротивления, которые, вероятно, помогут понять загадочную "сверхпроводимость" и создать наиболее адекватную модель этого необыкновенного явления.

1. Электрические заряды в проводниках. Так как вещества в принципе способны воспринимать электрические и магнитные поля и даже намагничиваться, то, следовательно, в их атомах есть диполи (микромагнитики) с положительными и отрицательными полюсами. Если эти диполи сориентировать (развернуть) положительными полюсами к поверхности, а отрицательными полюсами вовнутрь тела, то получаем у него положительные заряды, и, наоборот, если в сторону поверхности направлены отрицательные полюса диполей, то имеем отрицательно заряженное тело с таким же электрическим полем вблизи его поверхности. Если же диполи сориентированы вдоль вытянутого проводника, т. е. если сформировать упорядоченную дипольную структуру, направленную вдоль проводника, то получаем суммарное магнитное поле, параллельное проводнику.

Диполь состоит из двух точечных (единичных) зарядов: положительного и отрицательного. Носителем точечного заряда в проводнике является электрон. Следовательно, в диполе два электрона и два заряда, значит, суммарный заряд диполя равен зарядам двух электронов, а элементарный квант энергии диполя равен 2е. В теорию "сверхпроводимости" эти сдвоенные в диполе электроны с квантом энергии электромагнитного поля, равным 2е, ввел в 1956 г. американский ученый Л. Купер, поэтому их стали называть куперовскими парами (Л. Купер - Нобелевский лауреат 1974 г.).

2. Электрическое и магнитное поля. Статическое электрическое поле как посредник между заряженными телами отталкивает их или притягивает друг к другу. Оно, а не электроны и даже не диполи является энергоносителем, осуществляющим взаимодействие заряженного тела с другим заряженным телом или с исходно нейтральным, но заряжающимся телом под влиянием электрического поля предварительно заряженного тела.

При продвижении (перемещении, распространении) и изменении напряженности электрического поля у него появляется магнитная составляющая (магнитное поле), а вместе они представляют собой электродвижущее электромагнитное поле. Это обобщенное поле, как и статистическое электрическое, является носителем переменной электромагнитной энергии, распространяющейся по проводнику, хотя непосредственным источником этой энергии являются диполи, состоящие из спаренных и связанных с атомами, а не свободных электронов.

3. Электрический ток проводимости - это перенос потенциальной электрической энергии электромагнитного поля по проводнику к объекту преобразования ее в тепловую, механическую и другие виды энергии, а также в энергию радиоволн, в энергию света и т. д. Распространение полевой электромагнитной энергии по проводнику происходит как частично, внутри проводника, так и, в существенно большей мере, по материальному пространству вблизи проводника.

4. Электросопротивление. Очевидно, что электросопротивление распространению электромагнитной энергии вдоль проводника обусловлено не столкновениями свободно движущихся электронов с атомами токопроводящей среды, так как таких электронов в проводнике просто нет.

Известно, что основная часть электрической энергии находится не в проводнике, а вблизи него. В этом отношении проводник выполняет роль естественного направляющего для тока. Наибольшие затраты энергии тока проводимости, по-видимому, идут на создание упорядоченной субмикроструктуры диполей токопроводящего вещества и на некоторый разогрев в связи с этим. Разогрев состоит в усилении колебаний атомов, а это приводит к частичному разрушению созданной в проводнике дипольной субструктуры, которую приходится постоянно восстанавливать. Этот процесс разрушения и воссоздания субструктуры диполей происходит только тогда, когда есть энергопередача, называемая электрическим током. Очевидно, в этом заключается основная суть электросопротивления.

Вероятно, изложенные здесь альтернативные представления о зарядах, энергетических полях, электрическом токе, электросопротивлении могут стать основой для создания новой, уточненной теории электричества и послужат предпосылками для разработки адекватной теории физических явлений, происходящих в материалах при сверхнизких температурах.

3.2. Неадекватность гипотезы о физической природе
электрической "сверхпроводимости"

Проблема "сверхпроводимости" оказалась труднейшей для науки ?? столетия. По своей нерешенности и значимости она сопоставима с проблемой термоядерного синтеза. Есть мнение, что "проблема сверхпроводимости тормозила прогресс электронной теории металлов" [123.С.8], и, наоборот, установившаяся в физике "электронная теория металлов" и других веществ не допускала возможности создания альтернативной и, возможно, более правильной теории "сверхпроводимости".

Хорошо известно, что "сверхпроводимость" вначале рассматривалось учеными как "идеальная проводимость" электронного газа в толще проводника. Предполагалось, что строение (структура) проводника (металла) состоит из двух элементов: из ионно-кристаллической решетки и находящихся в металле (среди ионов) свободных, т. е. не связанных с ионизированными атомами, электронов, представляющих собой электронный газ из множества отдельных электронов. И, следовательно, считается, что электрический ток в металлическом проводнике - это направленное движение этих свободных электронов, а электросопротивление - результат столкновений электронов с колеблющимися ионами кристаллической решетки или другой некристаллической, например аморфной структуры.

Если считать, что при температуре 0 К тепловое движение ионизированных атомов вещества прекращается полностью, то их размеры не становятся при 0 К бесконечно малыми, а имеют значительную величину. Кроме того, в силу теплового изменения межатомных расстояний в твердом теле, плотность атомов при уменьшении температуры увеличивается, и поэтому количество столкновений и взаимодействий электронов с атомами не может уменьшиться до нуля. Следовательно, электросопротивление R в зависимости от температуры Т должно записываться следующим уравнением:

0x01 graphic
,

где R₀ - минимально возможное электросопротивление;

? - коэффициент пропорциональности.

Коэффициент пропорциональности ? может быть постоянным для некоторых материалов или зависящим от температуры, но в любом случае, в соответствии с теорией электронного газа, при Т=0 К, R=R₀=const.

Однако вышеприведенная формула для R неверна по существу, так как электроны, обладая волновыми свойствами, не сталкиваются, как бильярдные шары, а если движутся, то взаимовлияют, взаимодействуют со своими как-то самопроизвольно ионизированными атомами проводника, и поэтому данная формула не соответствует действительности и она должна быть совершенно другой. Это свидетельствует о несостоятельности модели "электронного газа свободных электронов в проводнике". Данная модель и другие известные микроскопические модели электрического тока и "идеальной сверхпроводимости" электронов не объясняют ни "полного отсутствия сопротивления электрическому току в сверхпроводниках", ни скачкообразного исчезновения электросопротивления при температурах ниже Т_кр.

Поэтому нельзя не согласиться с В. Л. Гинзбургом, утверждавшим еще в 1946 г., что "дальнейших успехов теории сверхпроводимости можно ожидать, по-видимому, лишь на пути... количественного описания сверхпроводимости и развития теории, не прибегающей к представлениям об электронном газе металлов" [9.С.175].

Я. И. Френкель в своей работе "Сверхпроводимость", изданной в 1936 г., показал, что свободные электроны в проводнике "можно приближенно трактовать как газ с теплоемкостью, прямо пропорциональной абсолютной температуре". Теплоемкость проводника должна состоять из двух составляющих: из теплоемкости атомов и свободных электронов. Анализируя теоретические и экспериментальные результаты, Я. И. Френкель пришел к выводу, "что в отношении своей теплоемкости тело в сверхпроводящем состоянии ведет себя как диэлектрик, т. е. так, как если бы в нем вовсе не было свободных электронов. Другими словами, переход в сверхпроводящее состояние оказывается связанным со своеобразным изменением агрегатного состояния электронов, обуславливающих электрическую проводимость тела, а именно из состояния, аналогичного газообразному или жидкому, выше температуры "скачка" эти электроны переходят в какое-то иное состояние, при котором они, с одной стороны, оказываются как бы связанными с атомами, так же как и в диэлектриках, а с другой стороны, оказываются способными перемещаться по объему тела без всякого отклонения (выражающегося в электрическом сопротивлении тела), невзирая на тепловое движение его атомов" [111.С.15].

Так появилось представление о переходе в сверхпроводящее состояние как о кристаллизации электронного газа в своего рода кристаллическую электронную решетку. Представление об электронной решетке в металлах (наряду с атомной) развивалось в связи с попытками объяснения сил сцепления атомов в металлах. Гипотеза конденсации и кристаллизации электронов в металлах при их переходе в "сверхпроводящее" состояние не получила развития. Взамен трехмерной электронной кристаллической решетки, способной скользить без сопротивления сквозь решетку металлических ионов, появилось представление об одномерных электронных цепочках, способных скользить по атомным цепочкам кристаллической решетки.

Я. И. Френкель писал: "К аналогичному представлению об одномерных электронных цепочках, скользящих по цепочке ионов, как по конвейеру, пришел и я" [111.С.16]. Не анализируя подробно идею о "сверхпроводящих электронных цепочках", легко перемещающихся по атомным цепочкам кристаллической решетки, отметим только следующее. Проводники и "сверхпроводники" обычно состоят из множества кристаллических зерен, по-разному (хаотически) ориентированных. Поэтому "конвейера" вдоль проводника или "сверхпроводника" не может быть, так как развернуть кристаллы зерен, да еще без сопротивления (не затрачивая колоссальной энергии), нельзя. И второе замечание: если отдельные электроны перемещаются в проводнике с сопротивлением, то необъяснимо, как могут цепочки электронов перемещаться в проводнике без сопротивления среды. Если не будут устранены отмеченные и другие противоречия, то идея электронной конденсации в сверхподвижные цепочки не получит развития и подтверждения. Но эта идея не исчезла, а существенно изменилась в виде конденсации электронов в пары в момент перехода тел в "сверхпроводящее" состояние.

В работе [25] есть информация о том, что о существовании двухэлектронных биполярных состояний писал Р. А. Огг еще в 1945 г., который наблюдал аномально высокую проводимость в биполярных металл-аммиачных растворах, замороженных в жидком азоте. В 1946 г. Р. А. Огг утверждал, что ток, индуцированный в кольце из замороженного раствора натрия, в аммиаке не затухает в течение нескольких минут, что соответствует падению сопротивления на семнадцать порядков по сравнению с электросопротивлением раствора в жидком состоянии. Кольцо из замороженного раствора помещалось в электромагнит (Н - 15 000 Гс), и после отключения внешнего магнитного поля наблюдалось магнитное поле вблизи кольца в течение 1-2 мин.

Опыты Р. А. Огга в 1973 г. повторили И. М. Дмитренко и
И. О. Щеткин. Традиционно считается, что это были первые эксперименты по обнаружению относительно высокотемпературной (при 77 К) "сверхпроводимости". Опыты Р. А. Огга и других ученых аналогичны опытам Оннеса с кольцеобразным образцом из твердой (замороженной в жидком гелии) ртути. Отметим еще раз, что во всех этих случаях с б?льшим основанием следует утверждать об открытии экстремальных намагничиваемостей образцов.

А. С. Давыдов в работе [38] писал, что М. Шафрот в 1951 г. указал на невозможность объяснить "эффект Мейсснера", если в качестве начального выбрать состояние, не содержащее связанных пар электронов. А в 1956 г. американский физик Л. Купер предложил следующую описательную модель взаимодействия электронов с решеткой. Когда отрицательно заряженный электрон движется среди противоположно заряженных ионов решетки, то он поляризует решетку, т. е. притягивает к себе ближайшие ионы. При этом локально возрастает плотность положительного заряда, электрон как бы окутывается облаком (полем) положительного заряда, и к этому облаку притягивается второй электрон, в свою очередь, несущий "на себе" область поляризации решетки. Возникающее взаимное притяжение прежде свободных электронов связывает электроны в пары, получившие впоследствии название куперовских пар [41]. При таком описании процесса образования куперовских пар возникает ряд принципиальных вопросов: почему и как легкие электроны притягивают к себе тяжелые и закрепленные в решетке ионы, а не наоборот? Почему поток электронов выстраивается попарно, а не в последовательные цепочки, как по Я. И. Френкелю? И вообще, при переходе к "сверхпроводимости" электроны вряд ли спариваются, так как они существуют в атомах в форме диполей - двух связанных электронов с различными спинами. Заметим, кстати, что за предложение и разработку идеи о спаривании электронов при переходе к "сверхпроводимости" Л. Купер был удостоен Нобелевской премии.

В пятидесятые годы прошлого века академик Л. Д. Ландау и член-корреспондент АН СССР В. Л. Гинзбург предприняли попытку создания теории "сверхпроводимости" как сверхтекучести свободных электронов в металлах. Вот что тогда писал В. Л. Гинзбург: "Глубокая аналогия, существующая между сверхтекучестью и сверхпроводимостью, очевидна... Явление сверхпроводимости может рассматриваться как сверхтекучесть электронной жидкости в металле" [29.С.158]. Такое мнение о "сверхпроводимости" возникло в связи с тем, что П. Л. Капица обнаружил сверхтекучесть гелия при криогенных температурах, близких к абсолютному нулю. Так в теории "сверхпроводимости" возникла новая гипотеза, в которой электронный газ единичных и/или спаренных электронов был заменен электронной жидкостью, способный двигаться в проводнике без сопротивления. За это П. Л. Капица удостоен Нобелевской премии в 1978 г.

Так как сверхтекучесть была взята в качестве аналога "сверхпроводимости", то необходимо здесь кратко рассмотреть суть явления сверхтекучести изотопа гелия ⁴Не без трения о соприкасаемую поверхность.

В 1937 г. П. Л. Капица обнаружил, а в 1947 г. опубликовал, что жидкий гелий II (⁴Не) способен легко, самопроизвольно протекать через капилляры и щели, так как, во-первых, размер этих атомов гелия при температурах порядка 1-2 К по расчетам сравним с межатомными расстояниями твердых тел. Обычный атомарный гелий имеет атомное число 2, а его изотоп ⁴Не - это, по-существу, спаренный гелий из двух атомов. Свойства этого изотопа существенно отличаются от свойств ²Не и ³Не тем, что в нем две пары электронов, т. е. два диполя, которые компенсируют магнитные поля друг друга, и, возможно, поэтому ⁴Не становится, с одной стороны, не просто инертным, а наиболее нейтральным по отношению к находящимся поблизости другим атомам. Однако атомы подложки, отверстий, щелей, т. е. поверхностей любых твердых тел являются (в силу большой внутренней энергии) поверхностно-активными по отношению к практически нейтральному ⁴Не, притягивают его к себе с силой Р, и смачиваемость поверхности оказывается максимальной. С другой стороны, поверхностное напряжение ⁴Не, т. е. сила F кулоновского взаимного притяжения изотопных атомов ⁴Не, и коэффициент поверхностного натяжения ? близки к нулю. Так создается условие, что Р>>F, и поэтому жидкий ⁴Не становится "сверхтекучим". Но при всяком движении есть трение, есть процесс, уменьшающий энергию движения. В случае с ⁴Не сила трения намного меньше силы поверхностной активности атомов (Р) твердого тела, по поверхности которого течет жидкий гелий II и меньше силы поверхностного натяжения самого гелия. Поэтому создается впечатление, что это течение гелия происходит без трения. Аналогией здесь может быть спуск с горы на санках или на велосипеде без вращения педалей. Этот самопроизвольный спуск при равенстве сил трения и земного притяжения будет происходить при постоянной скорости, а спуск с крутой горы - ускоренно. Из этого не следует, что спуск происходит без трения. Так и в случае со сверхтекучестью гелия.

Такое объяснение сверхтекучести гелия II, т. е. ⁴Не, вполне согласуется с классической теорией капиллярных явлений жидкостей, и для этого не требуется вводить "элементарные возбуждения в жидком гелии II", которых почему-то нет в других жидкостях, в Не² и Не³, так как жидкий гелий II - единственная жидкость, в которой квантовые эффекты почему-то проявляются раньше, чем жидкость затвердевает.

Теоретическое объяснение сверхтекучести гелия II и связи между явлениями сверхтекучести и квантовыми свойствами жидкого гелия II было предложено Л. Д. Ландау еще в 1941 г. Квантовый характер жидкого Не⁴ обусловлен относительно слабым взаимодействием атомов гелия. В других жидкостях взаимодействие атомов достаточно сильное, поэтому они затвердевают до того, как появляются квантовые эффекты. В твердом теле при абсолютном нуле температуры атомы находятся в энергетически минимальном состоянии. При температурах, отличных от нуля, система атомов находится в возбужденном состоянии - атомы совершают колебания около положений равновесия. Далее следует: "Энергия кристалла будет суммой энергий квантовых осцилляторов. Каждый из осцилляторов при этом может находиться в каком-либо из возбужденных состояний. Вместо того чтобы говорить об осцилляторе в n-м возбужденном состоянии, можно рассматривать n колебательных квантов. Эти кванты - фононы - соответствуют звуковым волнам, подобно световым квантам - фотонам, представляющим волны света. Таким образом, состояние системы характеризуется совокупностью длинноволновых звуковых квантов - фононов. Фононы обладают энергией, которая линейно связана с импульсом (точнее, "квазиимпульсом"). Используя представление о фононах, можно объяснить все свойства твердых тел при низких температурах... Каждое элементарное возбуждение ведет себя подобно некоторой квазичастице, способной двигаться сквозь тело. Оно обладает определенной энергией и импульсом" [113.С.10-11].

Прежде чем продолжить цитирование источника [113], остановимся на изложенных началах теории сверхтекучести. В приведенной цитате есть несколько недопустимых подмен понятий. Колебание атомов кристалла подменено термином "осцилляторы", а последнее - колебательными квантами. Эти кванты переименованы в фононы, которые подобны квазичастице, способной двигаться сквозь тело. Так колебания (возбуждения) атомов превращаются в квазичастицы, обладающие собственной энергией Е и импульсом Р. И почему-то такая изначально запутанная теория "может объяснить все свойства твердых тел при низких температурах". Это странно и бездоказательно. Почему, собственно, все вышеприведенные в теории рассуждения о фононах твердого тела с необыкновенной легкостью перенесли на жидкий гелий II, как будто эти агрегатные состояния идентичны, не имеют принципиальных различий. Различие есть хотя бы в том, что атомы твердого тела имеют точки или "положения равновесия", а атомы жидкости, тем более сверхтекучей жидкости, такого "положения равновесия" не имеют, и поэтому, очевидно, в жидкостях нет придуманных в теории фононов.

Продолжим цитирование: "Малым импульсам соответствуют длинноволновые возбуждения, которые, как очевидно, в жидкости являются просто продольными звуковыми колебаниями. Таким образом, соответствующие элементарные возбуждения представляют собой звуковые кванты - фононы. Энергия фононов Е является линейной функцией импульса Р:

Е = с ? Р ,

где с - скорость звука.

...Дело в том, что одних фононов оказалось недостаточно для объяснения температурной зависимости и абсолютной величины таких характеристик, как, например, теплоемкость. Как легко видеть, элементарные возбуждения с энергией вблизи минимума... будут давать конкурирующий с фононами вклад во все термодинамические величины. Соответствующие возбуждения были названы ротонами" [113].

И далее: "Концепция элементарных возбуждений предполагает, что количество их невелико, так что энергия их взаимодействия между собой невелика по сравнению с собственной энергией. В этом случае газ элементарных возбуждений может рассматриваться как идеальный газ. ...При возбуждении жидкости фононы и ротоны могут появляться поодиночке. ...Фононный и ротонный газы описываются в равновесии... функциями статистики Бозе. ...При температурах порядка 1,7-1,8 К и ниже в гелии фононный и ротонный газы можно считать идеальными" [113.С.12,13]. Так возмущения, колебания атомов решетки чудесным образом поэтапно превращаются в фононный и ротонный идеальные газы. При этом остается все же непонятным, как эти ниоткуда появляющиеся при температурах 1-2 К газы связаны с атомами самой сверхтекучей жидкости - гелия II. Что сверхтечет - гелий II или мистические фононный и ротонный газы в нем? Поиск ответа приводит к мысли, что материальный гелий II опять-таки подменяется надуманными фононными и ротонными идеальными газами. Вот такая теория сверхтекучести перенесена с некоторыми дополнениями и изменениями на явление "сверхпроводимости". Не случайно поэтому о неприменимости теории возмущений для описания свойств "сверхпроводников" впервые говорил в 1951 г. физик М. Шафрот, указавший, в частности, что эта теория не может объяснить эффект Мейсснера ни в каком конечном порядке теории возмущений. К аналогичному выводу пришел в 1960 г. физик-теоретик А. Б. Мигдал, показавший, что в рамках теории возмущений в системе электронов нет энергетической щели для объяснения эффекта Джозефсона [38].

Еще "в 1933 г. К. Я. Гортер и Х. Казимир предполагали двухжидкостную модель сверхпроводящего состояния электронов проводимости металлов, в соответствии с которой при переходе в сверхпроводящее состояние не все электроны становятся сразу сверхтекучими, а только часть их, зависящая от температуры. В соответствии с моделью Гортера-Казимира в сверхпроводнике при температурах ниже критической существуют как бы две электронные жидкости - нормальная (N) и сверхпроводящая (S), определяющие все необычные свойства сверхпроводника. Соотношение между плотностями (количеством) этих электронных компонент изменяется с температурой. Во многих случаях двухжидкостная модель оказывается полезной для качественного анализа" [24]. При таком представлении о двухжидкостной электронной "сверхпроводимости" электросопротивление не должно было становиться нулевым за счет прохождения по проводнику части электронов нормальной проводимости, т. е. с сопротивлением их движению.

Почти двадцать пять лет спустя после К. Я. Гортера и Х. Казимира несколько иную двухжидкостную теорию "сверхпроводимости" развили в 1957 г. американские ученые Дж. Бардин, Л. Купер и Дж. Р. Шриффер, ставшие позднее лауреатами Нобелевской премии. Их теория получила аббревиатуру БКШ. В основу математического обоснования теории БКШ положены методы, развитые нашим соотечественником Н. Н. Боголюбовым.

Дж. Р. Шриффер в обстоятельной монографии [122] написал, что "в сверхпроводящем состоянии конечная доля электронов сконцентрирована в "макромолекулу", т. е. "сверхтекучую жидкость", распространенную на весь объем системы и способную к движению как целое. При нулевой температуре конденсация является полной, и все электроны участвуют в формировании этой сверхтекучей жидкости... При увеличении температуры часть электронов "испаряется" из конденсата и образует слабо воздействующий газ возбуждений (или "нормальную жидкость"), который также распространяется на весь объем системы; нормальный и сверхпроводящий компоненты при этом проникают друг в друга. Когда температура приближается к критическому значению Т_с, доля электронов, остающихся в сверхтекучей жидкости, стремится к нулю, и система претерпевает фазовый переход второго рода из сверхпроводящего состояния в нормальное. Эта двухжидкостная картина, описывающая свойства сверхпроводника, формально аналогична картине, характеризующей сверхтекучий ⁴Не, хотя между этими системами и имеются важные различия".

Далее читаем, что "микроскопическую теорию сверхпроводимости, предложенную Бардиным, Купером и автором, можно изложить на языке подобной двухжидкостной картины. В первом приближении сверхтекучая жидкость образована из электронных пар, связанных силами поляризации решетки. Эти пары сильно перекрываются в пространстве... Согласно теории, нормальная жидкость образована газом элементарных возбуждений системы" и т. д.

Приведем здесь только некоторые суждения об этой теории.

-- "Микроскопическая теория Бардина-Купера-Шриффера (теория БКШ) утверждает, что сверхпроводимость металлов обусловлена образованием связанных состояний электронных пар. Как же может возникнуть притяжение между такими двумя одинаково заряженными частицами, как электроны в металле? Теория БКШ объясняет этот феномен взаимодействием электронов с решеткой. Однако соответствующие вычисления не основываются на наглядных физических представлениях" [74.С.61-62].

-- "К сожалению, теория БКШ не отвечает на вопрос, почему не все металлы являются сверхпроводниками, и она не может предсказать сверхпроводящие свойства того или иного металла или сплава. Константа электрон-фононного воздействия V, входящая в основное уравнение энергии конденсации пар, не определена через известные микроскопические параметры металла и остается неизвестной" [41].

К настоящему времени известно несколько модификаций теории БКШ. Считается, что результаты физико-математической части теории БКШ получаются гораздо проще с помощью теории Гинзбурга-Ландау и отличаются числовыми значениями коэффициентов.

Наконец, следует упомянуть о выдвигавшемся в 1980 г. рассмотрении "сверхпроводимости" в обобщенной модели "желе" [26].

В качестве выводов из вышеизложенной информации можно констатировать, что ни одна из предлагавшихся моделей (микроскопических теорий) "сверхпроводимости" не является удовлетворительной и приемлемой. Те разнообразные понимания "сверхпроводимости", которые были и есть, исходят из навязчивой идеи (априорного постулата) о том, что в "сверхпроводнике" электроны в любом виде и состоянии должны непременно куда-то течь, перемещаться - и в обычном проводнике, и (по аналогии) в "сверхпроводнике", тогда как многие факты противоречат этому представлению. Поэтому возникает устойчивое альтернативное умозаключение о том, что электроны атомов не текут внутри и вдоль проводника или спиралеобразно, а с ними происходит в атомах нечто другое. Во всех микроскопических теориях проводимости и "сверхпроводимости" электроны, хоть и взаимодействуют со своими атомами, но существуют в проводнике самостоятельно, свободно, вне своих атомов и как вторая субстанция. Все же наиболее вероятно, что это не так, что все электроны находятся внутри своих атомов и, следовательно, не движутся, не текут впереди или за электромагнитным полем, распространяющимся по проводнику, а только передают его под действием соответствующего полевого напряжения.

3.3. Краткий анализ феноменологических теорий "сверхпроводимости"

Феноменологизм (от греч. phainomenon - явление) - методологический подход, принцип познания, согласно которому теория имеет дело только с явлением (феноменом) как таковым, как "непосредственно данным", наблюдаемым, а не с его сущностью, не с "вещью в себе", которая в такой теории остается скрытой и непознанной до конца. Феноменологическая теория создается на основе умозрительных представлений о фактах (свойствах) явления, на предположениях (постулатах), принимаемых в качестве фактов. Такая теория, не касающаяся сущности (внутренней природы) описываемого явления, носит общий, макроскопический подход. Но, как известно, "сущность является, а явление есть реализация сущности". Поэтому, в частности, научно обоснованная физическая теория должна сочетать в себе две взаимосвязанных части - микроскопическое и макроскопическое (феноменологическое) описание исследуемого явления. Однако, феноменологическая теория любого физического явления (процесса) должна основываться на фактах и на объективных результатах микроскопического, то есть сущностного, описания (микроскопической теории) исследуемого объекта. В качестве исходных предпосылок, априорных предположений или постулатов у правильной феноменологической теории могут быть только логические выводы и возможные (наиболее вероятные) научнообоснованные предположения, а не произвольно выдуманные. Истинность любой, в том числе и феноменологической, теории, её правильность, достоверность и адекватность, как известно, подтверждаются практикой (опытом, экспериментами, наблюдениями). Если феноменологическая теория физики "не освещает путь практике", не предсказывает, не обеспечивает, то есть не дает возможности количественно рассчитать свойства исследуемого объекта, то такая "теория" (точнее говоря, гипотеза) не может считаться теорией, то есть систематизированным знанием, подтвержденным экспериментально (практикой).

Обычно феноменологические макроскопические теории чрезмерно математизированы. Применение абстрактной математики при описании конкретной объективной реальности без тщательного учета внутренней природы исследуемого объекта, то есть в отрыве от его физической сущности и от количественных характеристик свойств приводит к нереальным, ошибочным результатам.

Внедрение в научную физику абстрагированных, математизированных макроскопических, то есть феноменологических, теорий привело к кризису в физике (см. [67]), который состоит в том, что содержание, сущность описываемого ими объекта заменяется символами, знаками и произвольными математическими действиями (операциями) с этими символами, знаками, допущениями, исключениями и т. д.

В классической работе В. И. Ленина [67] показано, что "кризис в физике состоит в завоевании физики духом математики... Теоретическая физика стала математической физикой... Элементы, в качестве реальных, объективных данных, т. е. в качестве физических элементов, исчезли совершенно. Остались только формальные отношения, представляемые дифференциальными уравнениями... "Материя исчезает", остаются одни уравнения... Разум предписывает законы природы" [67.C.329].

Вероятно, апофеозом идеологии феноменологизма в физике можно считать суждения академика Л. Д. Ландау, изложенные им в статье "О фундаментальных проблемах" (1960 г.). Там написано так, что при создании теории "мы вынуждены находить аналитические свойства..., исходя из гамильтонова формализма. Однако нужно быть очень наивным, чтобы пытаться придать "строгость" таким выводам; нельзя забывать, что мы получаем реально существующие уравнения из гамильтонианов, которые в действительности не существуют.

Мне кажется, что за последние годы теория заметно прогрессировала в указанном направлении и недалеко то время, когда будут окончательно написаны уравнения новой теории.

Нужно, однако, иметь в виду, что в этом случае в отличие от ситуации, существовавшей ранее в теоретической физике, написание уравнений ознаменует не конец, а начало создания теории. Уравнения теории будут представлять собой бесконечную систему интегральных уравнений, каждое из которых имеет вид бесконечного ряда, и будет очень трудно работать с такими уравнениями.

Сейчас, конечно, невозможно представить, сколько констант в теории можно будет выбрать произвольно. Мы не можем даже исключить возможность того, что уравнения вообще не будут иметь решений, т. е. что в теории снова возникнет нуллификация. Это можно будет рассматривать как строгое доказательство нелокальности природы" [61.T.2.C.384].

К сожалению, корифей советской и мировой науки, академик Л. Д. Ландау предсказал нам безрадостную перспективу развития теоретической физики, то есть предложил тупиковый путь развития физических теорий на основе феноменологических принципов и абстрактных математических методов "построения" физических теорий конкретных объектов или явлений природы.

Первым основополагающим постулатом всех известных феноменологических теорий "сверхпроводимости" является априорное утверждение о том, что в "сверхпроводнике" самопроизвольно перемещаются электроны и этим образуют незатухающий электрический ток. Такое утверждение не является реальным фактом; оно не подтверждено прямыми измерениями или наблюдениями за потоком электронов и поэтому не может приниматься в качестве объективной предпосылки для логического создания феноменологической теории "сверхпроводимости". Экспериментально наблюдаемым фактом является незатухающее магнитное поле "сверхпроводника". Из этого и следует исходить.

Другие постулаты (исходные предпосылки, условия) феноменологических теорий также вызывают сомнения. Обратимся к этим теориям.

Первую феноменологическую теорию "сверхпроводимости" предложили в 1935 г. братья Ф. Лондон и Г. Лондон. Считается, что в своей теории Лондоны придерживались "двухжидкостной" модели "сверхпроводника", предложенной ранее К. Я. Гортнером и Х. Казимиром. По этой модели в "сверхпроводнике" якобы существуют электроны двух типов - "нормальные" электроны проводимости с концентрацией n_n(Т) и "сверхпроводящие" с концентрацией n_s(Т). Полная концентрация электронов n = n_n+ n_s. Концентрация "сверхпроводящих" электронов убывает с ростом температуры и обращается в нуль при Т=Т_кр, а при Т?0 она стремится к полной плотности электронов n. "Сверхпроводящий" ток обеспечивается незатухающим движением "сверхпроводящих" электронов, а нормальные при этом ведут себя обычным образом [46.С.27]. Странно, что здесь и во многих других источниках как бы доказательством "сверхпроводимости" являются слова: "Сверхпроводящий ток обеспечивается незатухающим движением сверхпроводящих электронов". Это же логическая тавтология - тривиальная логическая ошибка в определении или в доказательстве "чего-либо через то же самое".

Судя по учебной литературе, в теории Лондонов часть признаваемой ими нормальной проводимости электронов в реальном "сверхпроводнике" почему-то не учитывалась. Теория абстрагирована от своей микроскопической модели. В противном случае общее сопротивление двухжидкостному току электронов в "сверхпроводнике" должно быть больше нуля, т. е. R?0, а в теории постулируется, что R=0. В этом состоит существенное внутреннее противоречие теории Лондонов.

Другим противоречивым постулатом первой феноменологической теории сверхпроводимости является то, что "теория Лондонов исходит из предположения, что вектор-потенциал электромагнитного тока в данной точке выражается через ток в той же точке". "Разработка макроскопических теорий сверхпроводимости и сверхтекучести не привела, однако, непосредственно к пониманию причин этих явлений, их внутреннего механизма, и вопрос о построении микроскопической теории, которая объясняла бы их исходя из основных законов квантовой механики, оставался открытым" [12.C. 298-299].

Можно прочитать, что Ф. Лондон в результате "напряженных размышлений" над странностью эффекта Мейсснера выдвинул следующее предположение: в сверхпроводнике под действием внешнего магнитного поля возникает "жесткая" упорядоченная волновая функция сверхпроводящих электронов, что и обеспечивает сверхпроводимость [41]. "Согласно теории Ф. и Г. Лондонов, сверхпроводимость является следствием "жесткости" волновой функции электронов по отношению к внешнему магнитному полю, а сам сверхпроводник как бы представляет собой "один большой диамагнитный атом" [122]. Предположения о потоке электронов (J?0), об отсутствии электросопротивления в "сверхпроводнике" (R=0) и о полном его диамагнетизме были заложены Лондонами в преобразования формул классической электродинамики, и "это стало основой для дальнейшего развития электродинамики сверхпроводников... Физик-теоретик Фриц Лондон первый указал, что для объяснения эффекта Мейсснера и существования постоянных сохраняющихся токов в сверхпроводящих кольцах необходимо предположить, что между электронами в сверхпроводнике имеется какая-то дальнодействующая связь и их движение оказывается скоординированным" [114.С.10]. "Ф. Лондон выдвинул... диамагнитную гипотезу, в которой сверхпроводник рассматривается, как гигантский атом с большим числом электронов... В каждой макроскопической теории имеются какие-либо необъясненные предпосылки. Так в теории Ф. Лондона и Г. Лондона остается неясным происхождение основных уравнений" [119.С.274-275].

При анализе любой теории на ее правильность надо исходить из законов формальной логики, по которым, если основополагающие утверждения не верны, то последующие теоретические построения (силлогизмы) и умозаключения не могут быть истинными. По такой причине теория Лондонов оказалась ошибочной, но ее все же многократно и практически малоэффектно пытались улучшать, "модернизировать".

Наиболее основательной переработке подверглась теория Лондонов в работах академиков В. Л. Гинзбурга и Л. Д. Ландау. Они в 1950 г. опубликовали (при отсутствии ясности в природе возникновения сверхпроводящего состояния [41]) свою феноменологическую теорию "сверхпроводимости" электронов, учитывающую "сверхтекучесть квантовых электронов", факт фазового перехода второго рода проводника в "сверхпроводящее" состояние, практически те же электрофизические постулаты и тезис о "жесткости" волновой функции ? движущихся в металле электронов, приняв, что 0x01 graphic

равняется плотности "сверхпроводящих" носителей зарядов n_s. При этом отмечается, что ограничивающим условием применимости теории Гинзбурга - Ландау является близость температуры образца к критической [29.С.34].

Но обратимся непосредственно к феноменологической теории "сверхпроводимости" академиков В. Л. Гинзбурга и Л. Д. Ландау.

В совместной работе академиков Л.Д. Ландау и В.Л. Гинзбурга "К теории сверхпроводимости", опубликованной в "Журнале экспериментальной и теоретической физики", N 20 (1064) в 1950 г., читаем, что не существует сколько-нибудь развитой микроскопической теории сверхпроводимости, однако феноменологическая теория процессов в сверхпроводниках находится в значительно лучшем состоянии и надежно базируется на уравнениях Ф. и Г. Лондонов [61.C.112]. И далее дословно: "При отсутствии магнитного поля переход в сверхпроводящее состояние, имеющий место при критической температуре Т_к, является фазовым переходом второго рода. В общую теорию таких переходов всегда входит некоторый параметр ?, отличный от нуля в упорядоченной фазе и равный нулю в неупорядоченной. Например, в случае сегнетоэлектрика роль ? играет спонтанная поляризация Р_S, а в случае ферромагнетиков - спонтанное намагничивание М_S. В сверхпроводниках, где упорядоченной является сверхпроводящая фаза, мы обозначаем характеризующий сверхпроводник параметр через ?. При Т > Т_к в состоянии термодинамического равновесия ? = 0, а при Т < Т_к ? ? 0. Мы будем исходить из того, что ? играет роль некоторой "эффективной" волновой функции "сверхпроводящих электронов". В соответствии с этим функция ? может быть определена лишь с точностью до произвольной постоянной фазы. Поэтому все наблюдаемые величины должны зависеть от ? и ?* таким образом, чтобы они не изменялись при умножении ? на постоянную типа е^ia.

Отметим также, что, поскольку количественная связь между ? и наблюдаемыми величинами еще не определена, мы можем нормировать ? произвольным образом. Ниже мы увидим, как можно выбрать эту нормировку для того, чтобы |?|² равнялся вводимой обычным образом концентрации "сверхпроводящих электронов" n_s" [61.С.114,115].

Как видно из приведенной цитаты, вначале авторы исходят из того, что переход метала в "сверхпроводящее" состояние есть, так называемый, фазовый переход второго рода, то есть это явление ни что иное, как изменение магнитных свойств путем поляризации Р_S электронных диполей в сегнетоэлектриках, а точнее говоря в сегнетомагнетиках, и намагничивания М_S опять-таки в результате поляризационного упорядочения ("выстраивания") электронной структуры атомов ферромагнетиков вдоль действия внешнего (даже земного) магнитного поля.

В данном случае исходно мы имеем магнитные свойства и их показатели стационарного состояния (поляризованности, намагниченности) электронов по отношению к их атомам. Но тут же авторы реальные, измеряемые показатели (Р_S и М_S) статического (неизменяющегося) состояния по своему желанию и произвольно подменяют некоторой абстрактной волновой функцией ?, но уже будь-то бы движущихся вдоль проводника "сверхпроводящих электронов", то есть функцией не для связанных, а свободно движущихся электронов в металле и почему-то без сопротивления этому интенсивному ("сверхтекучему") движению. Такие подмены (или подлоги) в научной логике считаются грубой ошибкой или умышленной подгонкой под желаемый результат.

С другой стороны авторы [61] по своему усмотрению наделяют придуманную ими функцию волновыми свойствами приписанными "сверхпроводящим электронам". Математическое написание этой функции основано на гипотетических предположениях, допущениях и т.п., а также на необоснованных, произвольно включенных математических действиях. А требуется, чтобы физические формулы были содержательными, то есть, чтобы они состояли из объективных показателей свойств и адекватных действий с ними. Только в таком случае формулы и теория могут быть правильными.

В последней книге Лауреата Нобелевской премии, академика В. Л. Гинзбурга [31] читаем, что учёные "в 1934 г. пришли к так называемому двухжидкостному подходу к сверхпроводимости...

В согласии с двухжидкостной картиной полная плотность электрического тока в сверхпроводнике

0x01 graphic
,

где J_s и J_n- соответственно плотности сверхпроводящего и нормального токов.

Нормальный ток в сверхпроводнике, по сути дела, не отличается от тока в нормальном металле и в локальном приближении

0x01 graphic
,

где E - напряженность электрического поля и ?_n - проводимость "нормальной части" электронной жидкости; в дальнейшем для простоты, если не оговорено противное, положим J_n=0.

В 1935 г. Ф. Лондон и Г. Лондон предложили для J_s уравнения (их называют уравнениями Лондонов)

0x01 graphic
,

где ? - некоторая постоянная" [31. С. 48].

И далее: "Если записать J_s в виде J_s = en_sv_s, где n_s - концентрация зарядов, то... при n_s = const

0x01 graphic
.

... При таком подходе основное уравнение Лондонов просто постулируется" [31. С. 49].

Со своей стороны добавим, что при e = const, n_s = const и v = const плотность тока сверхпроводимости J_s всегда имеет некоторое конечное значение, что противоречит представлению о "сверхпроводимости" как о токе с бесконечной проводимостью, с нулевым электросопротивлением и неограниченно большим током.

В. Л. Гинзбург писал: "В те далекие годы я продолжал рассматривать... вопросы теории сверхпроводимости... Было показано, что теория Лондонов приводит к неверным результатам при рассмотрении разрушения сверхпроводимости тонких пленок и при вычислении поверхностной энергии на границе между сверхпроводящей и нормальной фазами. Да и в целом стало ясно, что теория Лондонов непригодна в сильных полях Н, сравнимых с Н_c"[31.С.211].

В другом месте читаем: " Уравнения Лондонов сохраняют свое значение в настоящее время, но только в слабом поле

0x01 graphic
,

где Н_c- критическое магнитное поле, разрушающее сверхпроводимость (уравнения Лондонов несправедливы в условиях нелокальной связи тока с полем"[31. C. 49].

Однако "довольно широко распространено мнение, что феноменологическая теория процессов в сверхпроводниках надежно базируется на уравнении Ф. и Г. Лондонов"[31. С. 123]. "...Такой теорией, обобщающей теорию Лондонов, устраняющей отмеченные трудности и приводящей к ряду новых выводов, является ? - теория, построенная в 1950 г. В том же году мной был написан обзор, посвященный макротеории сверхпроводимости, включающей ? - теорию" [31. С. 50].

Но обратимся к ? - теории Гинзбурга-Ландау, основанной на ошибочной, несправедливой, постулированной и часто с неверными результатами.

В статье В. Л. Гинзбурга и Л. Д. Ландау " К теории сверхпроводимости", опубликованной в 1950 г., находим следующие основные положения ? - теории: "В сверхпроводниках, где упорядоченной является сверхпроводящая фаза, мы обозначим характеризующий сверхпроводник параметр через ?. При T > T_Kв состоянии термодинамического равновесия ?=0, а при T < T_K ??0. Мы будем исходить из того, что ? играет роль некоторой "эффективной" волновой функции "сверхпроводящих электронов". В соответствии с этим функция ? может быть определена лишь с точностью до произвольной постоянной фазы. Поэтому все наблюдаемые величины должны зависеть от ? таким образом, чтобы они не изменялись при умножении ? на постоянную типа exp (ia).

Отметим также, что поскольку количественная связь между ? и наблюдаемыми величинами еще не определена, мы можем нормировать ? произвольным образом. Ниже мы увидим, как нужно выбирать эту нормировку для того, чтобы |?|² равнялся вводимой обычным образом концентрации "сверхпроводящих электронов n_s". ...В состоянии равновесия... должно быть |?|²= 0 при T ™ T_K и |?|²> 0 при T < T_K. ... В состоянии равновесия при T © T_K

0x01 graphic
,

где учтено, что в пределах справедливости... ?(Т)=(d?/dT)_K и ?(T)=?_K выбор знака ? у ? определяется соображениями удобства". И далее: "... Дело, однако, в том, что введенная выше ? - функция отнюдь не является истинной волновой функцией электронов в металле, а есть некоторая усредненная величина"[31. С. 125-127].

С другой стороны по ?-теории "в сверхпроводнике течет ток, определяемый величиной |?|², пропорциональной концентрации "сверхпроводящих электронов" [31. С. 211].

Судя по вышеприведенным цитатам ?-теория Гинзбурга-Ландау отличается от феноменологической теории братьев Лондонов тем, что вместо концентрации, то есть плотности "сверхпроводящих электронов" в токе сверхпроводимости 0x01 graphic

введен неопределенный параметр ?, то ли как "волновая функция", то ли как "некоторая усредненная величина" концентрации сверхпроводящих электронов в теле.

Итак, "теория сверхпроводимости Гинзбурга-Ландау", как и все другие, полна противоречий и поэтому она не может считаться правильной научной теорией.

"В теории Гинзбурга и Ландау не выяснен смысл функции ? и связь ее с истинными волновыми функциями электронов в металле и не объяснена связь основных параметров ? и ? с микроскопическими характеристиками сверхпроводников (так, в частности, ничем не обоснована необходимость увеличения ? (диамагнитной восприимчивости) с ростом количества примесей в металле)" [119. С. 274]. Существуют и другие замечания к теории Гинзбурга - Ландау.

Академик А. А. Абрикосов в 1957 г., использовав теорию Гинзбурга-Ландау, как теорию фазового перехода вещества второго рода, создал свою теорию "сверхпроводимости" второго рода.

Он предположил, что при "сверхпроводимости" энергия границы раздела между предполагаемыми нормальной и "сверхпроводящей" фазами двухжидкостной модели ?_nsможет иметь как положительное (?_ns> 0), так и отрицательное (?_ns< 0) значение. Но энергии и вообще чего-либо меньше нуля, то есть меньше ничего, не бывает. Однако считается, что "сверхпроводники" с ?_ns> 0 - это сверхпроводники первого рода. А сплавы и химические соединения, которые тоже являются "сверхпроводниками", по Абрикосову, имеют ?_ns< 0 и поэтому они являются "сверхпроводниками" второго рода.

Очевидно, что если ?_ns> 0, то "сверхпроводимости" с R = 0 (? = 0) быть не может, так как эта энергия взаимосвязи между двумя различными потоками электронов, то есть между нормальным и "сверхпроводящим" потоками спаренных электронов, будет проявляться и создавать электросопротивление в силу различной скорости движения и передачи обычной (нормальной) и "сверхпроводящей" электрической энергии частиц с зарядами e и 2e.

С целью дальнейшего развития феноменологической части теории "сверхпроводимости" в том же 1957 г. Дж. Бардин, Л. Купер и Дж. Шриффер (США) предложили свою теорию [4]. В основу математического обоснования теории Бардина - Купера - Шриффера (БКШ) положены методы, разработанные советским физиком-теоретиком и математиком Н. Н. Боголюбовым. Но в теории БКШ обобщены сомнительные результаты теоретических исследований их предшественников.

Л. Купер в 1956 г. предположил, что "сверхпроводящие" электроны по какой-то неизвестной причине не отталкиваются, а притягиваются друг к другу, образуя взаимосвязанное состояние. Связанная пара электронов получила название куперовской пары.

В теории БКШ просто утверждается, что учёт гипотетического электрон-фононного взаимодействия может при определенных условиях привести к притяжению отрицательно заряженных электронов, имеющих противоположные спины (разные направления вращения). Такие спаренные электроны должны обладать нулевым суммарным спином и вероятно нулевым зарядом. Если температура тела ниже соответствующей критической температуры Т_кр, то его спаренные электроны (по теории БКШ) скапливаются (конденсируются). Происходит будто бы так называемая бозе-конденсация. Далее утверждается, что течение такого конденсата (конгломерата) внутри тела, почему-то должно быть сверхтекучим, бездиссипативным, без сопротивления.

Итак, "сверхпроводимость" по теории БКШ представляется так. При T < Т_кр в "сверхпроводнике" создается конденсат куперовских пар электронов. Этот конденсат обладает необычным свойством сверхтекучести. Поэтому утверждается, что электрический ток должен без сопротивления распространяться в "сверхпроводнике", но не бозе-конденсатом, а очевидно свободными куперовскими парами электронов, так как признается - элементарный (единичный) носитель электрического тока "сверхпроводимости" имеет заряд 2е.

В теории БКШ собраны всевозможные допущения, гипотезы и предположения, которые, как было показано выше, далеки от истины. Эта теория кое-что по-своему и иллюзорно объясняет, но не может ничего предсказать, что, по-видимому, свидетельствует о ее несостоятельности. Однако Дж. Бардин, Л. Купер и Дж. Р. Шриффер за свою теорию "сверхпроводимости" получили Нобелевскую премию.

В феноменологической теории БКШ "авторы рассмотрели упрощенную схему, в которой запаздывающее взаимодействие электронов, переносимое фононами, заменено мгновенным взаимодействием электронов, имеющим резонансный характер около границы Ферми... Ввиду того, что сделанные в методе трёх авторов упрощения и приближения надлежащим образом не были обоснованы, возникли большие сомнения в убедительности разработанной ими теории. Указывалось также и на отдельные ее дефекты" [12. C. 305, 306].

После создания теории БКШ появилось несколько модификаций, "улучшающих и расширяющих область ее объяснений" [41].

Так, например, в работах Л. П. Горькова (1958 г.) предложен математический метод решения модельной задачи теории БКШ. Считается, что ему удалось расшифровать все параметры феноменологической теории Гинзбурга-Ландау и "указать её область применения". Так, по мнению некоторых ученых работами Л. П. Горькова у нас было завершено построение теории "сверхпроводимости" Гинзбурга - Ландау - Абрикосова - Горькова (теории ГЛАГ). Однако впоследствии, в связи с открытием и изучением "сверхпроводников" второго рода, пришлось включить в обобщенную теорию ГЛАГ так называемые микроскопические квантовые явления и поэтому сейчас саму "волновую функцию" ?, предложенную В. Л. Гинзбургом, рассматривают как квантовую (дискретную) переменную величину.

Итак, основания и соответствующие феноменологические теории "сверхпроводимости", рассматриваемые порознь и вместе, представляются логически противоречивыми, базирующимися на бездоказательных предположениях, допущениях и условностях не могут быть признаны удовлетворительными. Поэтому нужен другой подход, другая теория явления, обнаруженного как считается Г. Камерлинг-Оннесом еще в 1911 году.

Если представления и теории "сверхпроводимости" не верны, что следует из вышеизложенного, а само явление "сверхпроводимости электрического тока" не является таковым, т. е. не является идеальной проводимостью (сверхтекучестью) электронов в твердых телах, то, следовательно, для этого явления не подходит электродинамическое описание. Оно, будучи явлением магнетизма, что доказывает адекватное восприятие известных экспериментов, может и должно рассматриваться как явление полного или промежуточного метастабильного дианамагничивания тел. Переход от ферромагнетизма и парамагнетизма или от высокотемпературного диамагнетизма к промежуточному или полному диамагнетизму (к сверхдиамагнетизму), происходящий при температурах Т_кр, в действительности есть фазовый переход третьего рода, но не электронного конгломерата, а атомов твердого вещества. Механизм этого внутриатомного фазового перехода будет представлен далее.

Сейчас можно утверждать, что современные макроскопические (феноменологические) теории "сверхпроводимости" ничего не проясняют, а только запутывают представление о рассматриваемом ими явлении. Они не дают возможности расчетов каких-либо параметров, не позволяют делать предсказания и рекомендации для практического применения "сверхпроводников". В связи с этим, данные, излишне математизированные, теории, как чрезмерно сложные и, главное, практически бесполезные, не могут признаваться научными теориями, т.е. адекватными природе явления называемого "сверхпроводимостью" электрического тока.

3.4. Термодинамика и "сверхпроводимость"

Много принципиально новых фактов и закономерностей открыто при изучении свойств различных веществ при гелиевых температурах. Физикой низких температур установлено, что при понижении температуры, приближающейся к 0 К, в свойствах веществ проявляются особенности, которые при обычных температурах подавляются сильным тепловым движением атомов. К числу таких особенных явлений относятся так называемые "сверхтекучесть гелия Не⁴" и "сверхпроводимость электрического тока". При низкой криогенной температуре жидкий гелий Не⁴ претерпевает внутриатомное фазовое превращение (фазовое превращение второго рода), сопровождающееся значительным уменьшением вязкости, что было названо сверхтекучестью. При изучении "сверхпроводимости" обнаружено такое особенное свойство веществ, как способность создания с помощью "сверхпроводников" сильных магнитных полей, а также сверхчувствительных контактных устройств (контактов Джозефсона), реагирующих на слабые электрические напряжения и на очень малые изменения напряженности магнитного поля вблизи критической температуры Т_кр. Все эти и другие явления, возникающие при низких криогенных температурах, имеют термодинамическое происхождение, т. е. они обусловлены температурным фактором. Поэтому термодинамика веществ при низких температурах является ключевой в исследовании природы магнитных и других свойств атомов и веществ в целом.

Начала, принципы, основные законы термодинамики универсальны, и они имеют прямое, непосредственное отношение к рассматриваемой нами проблеме сверхнамагничиваемости веществ при закритически низких температурах.

Первый закон (начало) термодинамики формулируется так: изменение внутренней энергии ?U тела (системы) при переходе из одного состояния в другое равно сумме совершенной над телом работы А? и полученного им количества теплоты ?Q:

?U = А? + ?Q.

Если работу А?, совершенную над другим телом (системой) внешними силами, заменить равной ей численно, но противоположной по знаку работой А= -А?, совершенной самим телом (системой) над внешними телами, то

?Q = ?U + А.

Количество теплоты ?Q, которое получено телом (системой), расходуется на изменение внутренней энергии ?U и на работу А системы (тела) против внешних сил. В этом состоит содержание первого закона (начала) термодинамики.

Первый закон термодинамики - это, по существу, приложение закона сохранения энергии к процессам, связанным с переходом работы в теплоту и обратно.

Второй закон термодинамики - это принцип необратимости процессов, связанных с теплообменом при конечной разности температур (т. е. текущие с конечной скоростью), с трением (сопротивлением), диффузией, расширением газов в пустоту, выделением джоулевой теплоты и т. д. Такие процессы необратимы, так как они могут одновременно и самопроизвольно протекать только в одном направлении. Это положение Р. Клаузиус в 1850 г. сформулировал как невозможность процесса, при котором теплота переходила бы самопроизвольно от тел с малой температурой к телам с большей температурой. Иначе говоря, невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому телу.

Приведем второй закон термодинамики в формулировке Кельвина (У. Томсона): невозможен периодический процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

Из второго закона термодинамики и обобщения многочисленных опытов следует, что невозможно создание вечного двигателя в силу того, что всякое механическое движение (работа) происходит с потерей части своей энергии на преодоление сил сопротивления этому движению. Следовательно, принципиально невозможно вечное движение "свободных" электронов внутри каких-либо тел без сопротивления и без превращения части кинетической энергии потока электронов в теплоту.

Поэтому можно утверждать, что "сверхпроводимость" электрического тока, или "сверхтекучесть" электронов в теле без сопротивления не может быть, так как противоречит второму закону термодинамики, и в частности, известному закону Ома.

Второй закон термодинамики сформулирован для процессов, связанных с тепловыми (температурными) эффектами. Однако аналогичные законы природы реализуются и в других процессах. Известно же, что невозможно самопроизвольное течение жидкости снизу вверх; жидкость сама не может течь туда, где ее уровень больше; электрический ток распространяется в направлении от большего электромагнитного потенциала (напряжения) к меньшему, а не наоборот и т. д. Наконец, если нет перепада (разности) давлений, то нет и движения. Все это очевидно, тривиально и бесспорно, так как для любого движения, во-первых, необходим расходуемый источник энергии (движущая сила), а во-вторых, определенная форма (вид) движения материального объекта не бесконечна во времени и пространстве в силу действия закона взаимного перехода (преобразования) одной формы движения материи в другую (первый закон термодинамики). Следовательно, существующая сейчас теория "сверхпроводимости" с ее нулевым электросопротивлением противоречит термодинамике, всей физике и здравому смыслу.

Резюме: теория "сверхпроводимости" электрического тока как "сверхтекучести" в телах спаренных электронов (куперовских пар) ошибочна.

3.5. Термодинамика фазового перехода тел

к сверхдианамагничиваемости

Еще в 1934 г. В. Кеезом, С. Гортер и Н. Каземир попытались создать термодинамическую теорию перехода металлов в "сверхпроводящее" состояние как теорию фазовых переходов. Тогда было достаточно много аргументов в пользу такого подхода к изучению физической природы "сверхпроводимости". Например, есть зависимость "сверхпроводимости" от фазового состояния металла: белое олово "сверхпроводящее", а серое - нет. Многими опытами доказано, что "сверхпроводимость" бесспорно принадлежит к структурно чувствительным свойствам [76. С. 11]. Это на первый взгляд свидетельствует о подобии фазовым переходам первого рода, аналогичным 0x01 graphic

(

) превращением в железе. Однако позднее было установлено, что "какой-либо прямой связи между кристаллическим строением и сверхпроводимостью установить нельзя" [29. С. 13]. Определено, что картина дифракции рентгеновских лучей имеет один и тот же вид как выше, так и ниже критической температуры, что указывает на неизменность кристаллической решетки при переходе проводника из нормального в "сверхпроводящее" состояние. Микроструктурные исследования также показали, что кристаллическая структура металла (и других веществ) до перехода в "сверхпроводящее" состояние и после восстановления нормального состояния остается без изменений. Кроме того, этот переход не сопровождается выделением или поглощением тепловой энергии. Следовательно, рассматриваемое явление есть фазовый переход второго рода, а физическая природа его обусловлена, очевидно, не изменением межатомных или межмолекулярных взаимодействий, а изменением внутриатомной электронной структуры твердого тела при критической температуре, необходимой для этого фазового перехода.

Ясно, что валентные электроны внешнего пространственно-энергетического уровня, устанавливающие взаимосвязи атомов и формирующие микроструктуру (кристаллическую атомную или молекулярную) вещества, не претерпевают изменений при рассматриваемом фазовом переходе, так как при этом микроструктура тел остается неизменной.

Следовательно, можно думать, что, во-первых, оставшиеся валентные электроны, т. е. не задействованные на межатомные связи, обеспечивают свойство обычного магнетизма; во-вторых, дополнительную намагничиваемость при температурах ниже Т_кр, вероятно, создают спаренные в диполи электроны другого (низлежащего) уровня.

Убедившись в том, что различные твердые тела при очень низких температурах переходят от обычного (нормального) состояния к сверхнамагничиваемости, а не к "сверхпроводимости", и впоследствии в сверхнамагниченное состояние, в дальнейшем вместо слов "сверхпроводимость", "сверхпроводящее состояние", "сверхпроводники" будем использовать термины "сверхнамагниченность", "супер- или сверхмагнитное состояние", "сверхмагнетики", а также "сверхдиамагнетизм" и т. п.

Теперь обратимся к фактам и к термодинамическому рассмотрению перехода тел из нормального состояния в состояние сверхнамагничиваемости при температурах меньше Т_кр.

Очевидно, что при температуре Т, немного меньшей Т_кр, и в отсутствие магнитного поля, внутренняя энергия W_c тела, находящегося в состоянии способности к сверхнамагничиваемости, несколько меньше W_н, чем будучи в нормальном состоянии (при Т >Т_кр). При Т=Т_кр W_c-W_н, так как в теле не происходят какие-либо микроскопические изменения структуры. Поэтому отсутствие сколько-нибудь заметного температурного эффекта при свободном переходе тел от нормального состояния в состояние возможного сверхнамагничивания свидетельствует о том, что этот переход есть фазовый переход второго рода, обусловленный изменением субмикроскопического (внутриатомного) состояния вещества.

Если образец из сверхмагнетика вначале охладить до Т<Т_кр, а потом включить внешнее магнитное поле или начать пропускать обычный электрический ток (электромагнитный поток), то внутренняя энергия образца Q_пр будет состоять из W_c и энергии намагничивания W_c_м. То есть общая энергия прямого фазового перехода с намагничиванием равна

0x01 graphic
,

а при размагничивании (при Н ™ Н_кр, J ™ J_кр или при Т ™ Т_кр) энергия обратного перехода в нормальное состояние такова:

0x01 graphic
.

Из этих двух простых формул следует, что Q_пр>Q_об, т. е. что при сверхнамагничивании и размагничивании сверхмагнетика должна наблюдаться энергетическая петля гистерезиса.

Энергия сверхмагнетика - тела, способного к сверхнамагничиванию, - увеличивается при прямом превращении в сверхмагнитное состояние и уменьшается при обратном переходе в нормальное состояние. Поэтому если, например, разрушение сверхнамагниченности происходит под влиянием внешнего магнитного поля большего, чем Н_кр, то, в условиях адиабатической изоляции образца, он будет охлаждаться.

Измерения теплоемкости С сверхмагнетиков (по-старому "сверхпроводников") при отсутствии магнитного поля (Н=0) показали, что при снижении температуры теплоемкость в точке перехода Т_кр испытывает мгновенное увеличение до значений, которые примерно в 2,5 раза превышают ее значение в нормальном состоянии вблизи Т_кр. При этом теплота фазового перехода вещества

?Q = ?W_c - W_н? = 0.

Рассматривая тепловое движение одного атома в твердом теле, имеющего три степени свободы движения, получаем, что средняя энергия колебательного движения атома ? в теле равна

0x01 graphic
,

а на один килограмм-атом вещества приходится энергия

0x01 graphic
,

где N_о - число Авогадро; k - постоянная Больцмана; Т - температура; R - универсальная постоянная вещества (R=B?; В - постоянная величина, зависящая от природы тела, а ? - атомный или молекулярный вес вещества).

Темлоемкость С - это количество теплоты Q, необходимое для нагревания одного килограмм-атома твердого тела на один градус температуры. Следовательно, теплоемкость тела при определенной температуре равна

0x01 graphic
.

У твердых тел при обычных температурах С_н-25 кДж /кг-атом?град [47], а при температуре, равной Т_кр, С_с-62,5 кДж/кг-атом?град.

Зависимость теплоемкости С от температуры Т при переходе сверхмагнетика от его нормального состояния к состоянию сверхнамагничиваемости имеет известный вид, приведенный на рис. 6.

0x01 graphic

Рис. 6. Скачок теплоемкости сверхмагнетика в точке перехода (T_кр)
в отсутствие внешнего магнитного поля (С_с и С_н - теплоемкости
в сверхнамагничиваемом и в нормальном состояниях)

Немного перефразировав, можно сказать, что на рис. 7 приведены известные схемы фазовых диаграмм обратного перехода для сверхмагнетиков первого и второго рода.

0x01 graphic

Рис. 7. Виды фазовых диаграмм распада сверхнамагниченности

(схемы фазовых диаграмм обратного перехода в нормальное состояние) сверхмагнетиков первого (а) и второго (б) рода

Кстати следует заметить, что фазовых термодинамических диаграмм прямого перехода, т. е. перехода от нормального состояния в "сверхпроводящее", а по-нашему в сверхнамагниченное состояние, не существует. Но на основе имеющихся данных можно предположить, что такие термодинамические диаграммы перехода тел в состояние сверхнамагниченности имеют вид, показанный на рис. 8.

Рассматривая переход к сверхмагнетизму, следует обсудить здесь имеющиеся в литературе зависимости сверхнамагничивания М_с под действием постоянного магнитного поля Н. Есть несколько однотипных графиков зависимости М_с от Н, приведенных, например, в книгах [46. С. 45 и 119. С. 24]. Обобщенное изображение этих зависимостей показано на рис. 9, а, но такое представление сверхнамагничиваемости вызывает сомнение в его правильности. Во-первых, намагничение магнитным полем Н при уменьшении величины Н не снижает намагниченность М_с. В противном случае постепенное или ускоренное отклонение Н от сверхнамагниченного образца уничтожало бы его намагниченность, но этого не происходит. Во-вторых, намагниченность М_с всегда и намного больше внешнего поля Н. Поэтому график зависимости М_с от Н имеет, очевидно, вид, приведенный на рис. 9, б.

а б

Рис. 8. Вероятные схемы термодинамических диаграмм прямого перехода (т. е. от нормального состояния к сверхмагнитному) образцов

сверхмагнетиков первого (а) и второго (б) рода

а б

Рис. 9. Зависимость сверхнамагничивания первого рода
от действия внешнего магнитного поля Н

Схематически изображенная зависимость М_с от Н и ее скачкообразный характер фазового перехода образца в магнитном поле (рис. 9, б) наблюдается только в случае, когда охлажденный до температуры Т<Т_кр и обрабатываемый магнитным полем образец имеет вытянутую цилиндрическую форму и находится в продольном магнитном поле. При произвольной форме образца или большой массы и при иных ориентациях магнитного поля переход в сверхнамагниченное состояние оказывается растянутым в достаточно широком диапазоне значений Н<Н_кр. Это свидетельствует о том, что переход тел от нормального состояния (ферромагнитного, парамагнитного или диамагнитного) к состоянию сверхнамагничиваемости есть фазовый переход второго рода и что его физическая природа состоит не в межатомном, не в электрон-фононном и не в межмолекулярном взаимодействии, а обусловлена она в основном внутриатомными изменениями во взаимодействии парных электронов (диполей) между собой. Следовательно, должна быть не микроскопическая, а субмикроскопическая теория сверхнамагничиваемости тел, т. е. эта теория должна быть атомной, а способы перевода веществ в сверхмагнитное состояние надо считать не нанотехнологией, а пикотехнологией.

3.6. О недостоверности объяснений возникновения

"сверхпроводимости" электродинамической

индукцией "сверхтока"

Рассмотрим вопрос о научной достоверности объяснений и теорий возникновения и поддержания "сверхпроводимости" посредством электромагнитной индукции "сверхтоков".

Как уже отмечалось при объяснении эффекта "сверхпроводимости" утверждается, что "сверхток" индуцируется (возбуждается) в "сверхпроводнике" обычным и, в частности, постоянным электрическим током или постоянным магнитным полем. При этом необоснованно делается ссылка на законы и формулы классической электродинамики Фарадея-Максвелла. Но во времена М. Фарадея и Д. Максвелла о существовании "сверхпроводимости" еще не знали, а законы их электродинамики относятся только к обычному электрическому току с сопротивлением. Для описания "сверхпроводимости" электрического тока, который без электрического поля и без сопротивления, классическая электродинамика не пригодна. Следовательно, теория "сверхпроводимости" не может основываться на законах электродинамики М. Фарадея и Д. Максвелла.

М. Фарадей еще в 1831 году экспериментально доказал, что только переменный, импульсный (а не постоянный, как в случае со "сверхпроводниками") электрический ток возникает под влиянием внешнего, переменного во времени магнитного поля H_вн.Постоянный ток неподвижного проводника не индуцирует в соседнем проводнике электрического тока. В связи с этим М. Фарадей писал: "Была изготовлена составная катушка... однако независимо от того, как проходил ток от батареи... гальванометром не удавалось обнаружить никакого действия на другую катушку" [103. С. 13].

По М. Фарадею: "Присущее электрическому напряжению свойство создавать вблизи себя противоположное электрическое состояние получило общее название индукции. ... Целый ряд действий, вызываемых индукцией электрических токов, был найден, как то намагничивание. ... всякий электрический ток сопровождается магнитным действием соответствующей интенсивности, направленным под прямым углом к току" [103. С. 11-12]. Здесь у М. Фарадея речь идет не о индукции тока, а о магнитной индукции, в частности, о намагничивании вследствие электрического тока.

Позднее Джеймс Максвелл, развивая идеи Михаила Фарадея по электродинамике, писал: "Когда проводник перемещается вблизи электрического тока или магнита или когда электрический ток или магнит перемещаются вблизи проводника, или изменят свою напряженность, то в проводнике возбуждается (наводится, индуцируется) электродвижущая сила, вызывающая электрическое напряжение, или ток, смотря по тому, разомкнут проводник или же замкнут. Подобный ток возникает только при изменении электрического или магнитного состояния тел, окружающих проводник, и никогда не наблюдается, пока это состояние остается неизменным" [70. С. 61].

Из вышеизложенного следует, что существует два вида индукции:

1. Взаимная электродинамическая индукция как результат электромагнитного взаимодействия двух (возможно и нескольких) тел. Это воздействие одного тела на другое происходит через некоторое пространство между телами (дальнодействие) и поэтому является для них внешним взаимодействием, а такая индукция называется взаимной.

Д. Максвелл рассматривал несколько разновидностей взаимной индукции: взаимное действие изменяющихся токов двух проводников, индукцию одного тока другим, индукцию тока при относительном движении проводника с током и при относительном движении постоянного магнита по отношению к проводнику без тока, в котором индуцируется электрический ток. Во всех этих случаях возникает электродвижущая сила (Y) и, следовательно, электрический ток (I), а также появляются полевые силы притяжения или отталкивания проводников.

2. Самоиндукция - появление возбуждаемого магнитного поля в проводнике и вблизи его в связи с распространением по нему электрического поля (тока). Если ток в проводнике постоянный, то и его магнитное поле стационарно в пространстве и во времени, то есть неизменно. Если ток в проводнике переменный, то и магнитное поле проводника переменно по величине и по направлению. Этот вид индукции происходит по внутренней причине - от действия на материал проводника распространяющейся по нему электрической энергии, то есть от прохождения по проводнику электрического тока. При самоиндукции причина (ток проводимости) и следствия (появление магнитного поля Н) находятся внутри самого проводника. В этом принципиальное отличие магнитной самоиндукции проводника от электромагнитной взаимоиндукции непостоянного электрического тока и его изменяющегося (вторичного) электромагнитного поля.

В соответствии и вышеизложенным следует помнить, что в результате взаимоиндукции в проводнике возникает переменный электрический ток и соответствующее ему магнитное поле, а при самоиндукции в проводнике с током возникает постоянное или переменное магнитное поле. Электрический ток есть передача потенциальной энергии электрического поля от его источника к преобразователю и потребителю этой энергии. Иначе говоря, электрический ток это такое движение электрического поля по проводнику, которое приводит к появлению соответствующего магнитного поля и возможного намагничивания проводника.

Заметим, кстати, что если у проводника нет электрического поля, то, следовательно, по нему (или в нем) не течет электрический ток, как это наблюдается у материалов в "сверхпроводящем" состоянии.

В "Трактате об электричестве и магнетизме" (1873 г.) - в основном и фундаментальном труде Д. Максвелла, связь электрического и магнитного полей проводника с током математически выражена в наиболее общем виде [70]. Впоследствии, Дж. Томсон, Г. Герцен, О. Ховисайд и Х. Лоренц, развивая теоретические достижения Максвелла, привели к тому, что в электрофизике (раздел электромагнетизма) была получена система формул в векторном выражении, представляющая соотношение электрического и магнитного полей в проводнике с электрическим током проводимости. Эти теоретические уравнения, математически выражающие наблюдения Фарадея, были названы "уравнениями полей" или "уравнениями Максвелла", хотя они не все получены им и имеют несколько различных написаний. Такая система "уравнений Максвелла" в векторном представлении, претерпевшая несколько преобразований, утвердилась в науке в следующем, наиболее распространенном виде [71. С. 423]:

- векторные соотношения

0x01 graphic
, (1)

0x01 graphic
, (2)

0x01 graphic
, (3)

0x01 graphic
, (4)

0x01 graphic
, (5)

- скалярные соотношения (дополнительные уравнения)

D = ?E, B = ?H, J_пр = ?E ,

где:

- вектор внешнего магнитного поля,

- электрическая индукция,

- вектор магнитной индукции (у проводников B<H),

- вектор электрической напряженности,

- вектор плотности электрического тока проводимости,

? - плотность электрических зарядов,

?- магнитная проницаемость среды,

? - диэлектрическая проницаемость среды,

t - время,

c - скорость света,

? - электропроводимость.

Известно, что каждое векторное уравнение Максвелла внутренне содержит в себе три скалярных уравнения (для каждой из пространственных осей координат) со своими неизвестными функциями векторов 0x01 graphic

. Поэтому векторные уравнения Максвелла являются неопределенными и недостаточными для вычисления количественных значений установившихся электрических и магнитных полей в токопроводящем веществе. Общепризнано также, что система векторных уравнений Максвелла является неполной. Для того, чтобы произвести вычисления полей проводника с током в систему уравнений Максвелла включают соответствующие скалярные соотношения величин D, J и E, а также Н и В, что делает уравнения Максвелла описывающими стационарное электромагнитное состояние токопроводящего вещества, то есть описывающими не строго статическое (неподвижное), а состояние с постоянными и однонаправленным потоками полей, индуцируемых электрической энергией стабильно переносимой по проводнику.

Практическими ("материальными") формулами для расчета параметров полей проводника с током, то есть конкретизирующими уравнения Максвелла, используются следующие формулы:

D = ?E, B = ?H, J_пр = ?E, 0x01 graphic
.

Здесь и в формулах Максвелла (1) и (2) видно, что индукция магнитного поля В и индукция электрического противополя D есть по существу возникающие под действием электрического тока J_пр, то есть электрического Е и магнитного Н полей в теле (в проводнике или в диэлектрике), диамагнитные и диэлектрические свойства, создающие сопротивление электрическому току.

Считается, что поле В и связанное с ним поле D порождают так называемый электрический "ток смещения". Однако гипотетический противоток смещения практически не обнаруживается, потому что не существует. А существуют в проводниках с током J_пр (кроме Е и Н). D - диэлектрическое, то есть противоположное, противодействующее электрическое поле внешнему электрическому полю Е, а также противополе B - диамагнитное поле сопротивления внешнему полю Н, то есть полю H_и.

Необходимо отметить, что так как в формулах (1) и (2) системы уравнений Максвелла электрический ток проводимости 0x01 graphic

не зависит от времени, то есть является величиной постоянной, то, следовательно, поля Н, D, E и B тоже должны быть величинами постоянными. Поэтому уравнения Максвелла не являются правильными и не могут считаться математическим описанием соотношений полей у проводника со стабильным, в том числе и с постоянным электрическим током. Тем более эти уравнения не имеют отношения к "сверхтоку сверхпроводимости" с J_пр=?, так как его сопротивление считается равным нулю. Уравнения Максвелла не содержат показателя проводимости или электросопротивления. Это свидетельствует, что в теории Максвелла не рассматривается проблема электросопротивления и поэтому она не может иметь отношения к "сверхпроводимости". С другой стороны, отсутствие показателя электросопротивления в уравнениях Максвелла является их существенным недостатком, тогда как электросопротивление обусловлено самоиндукцией диэлектрического и диамагнитного полей, направленных против электромагнитного поля источника электрического тока в проводнике. Эти самоиндуцированные диэлектрическое и диамагнитное поля в проводнике с током были названы М. Фарадеем и позднее Д. Максвеллом "током смещения" и обозначены J_см. А по существу это как бы противоток, создающий электросопротивление току проводимости. Поэтому плотность тока проводимости J_пр есть разность (а не сумма J_общ=J_пр+J_см, как часто утверждается) между максимально возможным током J_возм (как при коротком замыкании) и гипотетическим "током смещения" в проводнике, то есть

где "ток смещения" равен [95. С. 228]:

0x01 graphic
.

В формуле для тока смещения J_см есть индукция электрического поля D, но нет показателя электросопротивления ?. Поэтому эта формула (по закону Ома) не может характеризовать ток смещения, так как любому току есть сопротивление.

Приведенные здесь более логичные формулы для токов в проводнике, но и они не соответствуют реальности, так как электрического тока не возникает, то есть не существуют одновременно и ток проводимости и ток смещения, противоположно направленный току проводимости. Из этого следует, что электрический ток, с его магнитным полем, индуцирует контрполяризацию атомов и определенное диамагнитное поле, противодействующее магнитному полю тока и самому электрическому току, что является электросопротивлением.

Заметим теперь, что приведенные выше векторные уравнения Максвелла не являются безупречно правильными. Правильность физических равенств первоначально проверяется по совпадению размерностей величин находящихся в уравнении слева и справа от знака равенства.

Очевидно, что единицы измерений сопоставляемых величин в системе уравнений Максвелла не удовлетворяют требованию их соответствия, так как в части формул приравниваются разные по физической природе (различные по смыслу) характеристики свойств. Так, например, в первых двух уравнениях Максвелла складываются величины электрических и магнитных полей, измеряемых в гауссах (Гс), с электрическим током, измеряемым в амперах (А), что недопустимо. Но в физике часто используют формалистически обобщенные не законы, а описания и "обтекания" трудностей при помощи математических средств. Этот прием использовал и Максвелл. По указанной причине в формулах Максвелла следует ставить не знак равенства, а знак ? - "влечет за собой" или знак ? - "эквивалентно", "подобно".

Следовательно, уравнения Максвелла, и другие видоизмененные записи его уравнений в символах векторной алгебры, не вполне адекватны истинной природе индукции полей. Придерживаясь принципа одинаковости (совпадения) размерностей равных компонент любого уравнения, легко убедиться в том, что все основные уравнения современной теории "сверхпроводимости" так же не удовлетворят этому обязательному физико-математическому требованию, а такая "теория" не может быть правильной.

Рассмотрение системы уравнений Максвелла на их удовлетворение формальному критерию соответствия размерностей позволяет утверждать, что этими формулами векторного математического анализа, только качественно, а не строго количественно и не точно, описывается физическая природа индукции электрического и магнитного полей в проводнике с электрическим током.

Анализ вышеприведенных уравнений Максвелла показывает так же, что они отражают взаимосвязь кинематических электрического и магнитного полей в проводнике со стационарным, переменным или постоянным током. Эти уравнения для полей разделяются на две группы: формулы (1), (2) и (4) выражают поля через их источники - электрические заряды и токи (ток проводимости и ток смещения), а формулы (3) и (5) источников тока не содержат и показывают связь между Е и В, то есть связь вне зависимости от свойств их источников.

В книге [104. С. 46] уравнения Максвелла преобразованы к виду:

(скалярное умножение),

(векторное умножение),

(скалярное умножение),

(векторное умножение),

где: ? - плотность электрического заряда, J - плотность электрического тока, ? - оператор набла (оператор Гамильтона).

Так как ? и J постоянные величины во времени, то данные уравнения преобразуются и разделяются на две группы:

- уравнения электростатики

0x01 graphic
,

0x01 graphic
;

- уравнения магнитостатики

0x01 graphic
,

0x01 graphic
.

Видно, что система уравнений Максвелла разделена на две части так, что электрическое поле Е есть только в первой паре уравнений, а во второй магнитное поле В. Между собой Е и В не связаны, а это означает, что, при постоянстве зарядов и тока, явления электричества и магнетизма разные, так как нет зависимости полей Е и В друг от друга. Этой зависимости нет до тех пор пока нет изменения в зарядах или токах, или пока вблизи проводника не начнет двигаться магнит с магнитным полем Н_вн. Из этого следует, что наличие постоянного магнитного поля В вокруг проводника не свидетельствует о нахождении в нем электрического тока. Можно утверждать, что только если у проводника одновременно есть постоянные В и Е, то по проводнику течет постоянный ток [71. Приложения. С. 423-424].

Следовательно, в уравнениях Максвелла есть только электрический ток проводимости и характеристики его полей.

Попытки применения уравнений Максвелла для описания "сверхппроводимости" в замкнутом контуре (например, в кольце) показывают, что, так как в экспериметах со "сверхпроводимостью" внешнее магнитное поле H_вн не изменяется во времени t, то при H_вн=const внутри кольцеобразного проводника rotB=0. При этом rotE=0, т.е. переменная электрическая напряженность в проводнике не возникает и, следовательно, тока взаимоиндукции не бывает. Отсутствие электрического тока проводимости внутри "сверхпроводника" не означает, что постоянный суперток в "сверхпроводнике" все-таки есть, но он почему-то из объемного становится приповерхностным.

Итак, очевидно, что законы электродинамики не применимы к постоянным электрическим токам, постоянным магнитным и электрическим полям, как в случае со "сверхпроводимостью". Однако в литературе утверждается, что так называемая "сверхпроводимость", все же возникает (индуцируется) в условиях действия постоянного во времени и по величине электрического тока или постоянного магнитного поля. Но ведь это тот "случай когда от времени ничего не зависит ... В таких условиях в уравнениях Максвелла все члены, являющиеся производными по времени, обращаются в нуль" [104. С. 68]. Приведенная цитата из классического труда "Феймановские лекции по физике" еще раз подтверждает, что теория электродинамики Максвелла не имеет отношения и не может быть основанием для теории "сверхпроводимости". А это означает ошибочность современной теории "сверхпроводимости" основанной на максвелловской электродинамической взаимоиндукции электрического тока, электрического и магнитного полей.

Далее. Известно, что у проводника с электрическим током всегда есть электрическое и магнитное поля (суммарное электромагнитное поле). Но еще "Камерлинг-Оннес установил, что в перешедшем в сверхпроводящее состояние образце - элементе электрической цепи с источником постоянной ЭДС, электрическое поле отсутствует" [111. С. 11]. Факт отсутствия электрического поля Е у образца, предполагаемого "сверхпроводящим электрический ток", легко установить. А если действительно, что в "сверхпроводящем" образце Е = 0, то есть если в нем "не возникает поле электрическое, не возникает и ток - даже в образце с нулевым удельным сопротивлением" [22. С. 275]. Это так. Следовательно, переход материала образца в "сверхпроводящее" состояние с Е = 0 делает его нетокопроводящим (изолятором), так как электрический ток есть следствие наличия электрического потенциала и перепада (разности) напряженности (потенциала) электрического поля (?Е > 0).

Однако, вопреки фактам, во всех феноменологических теориях "сверхпроводимости" (братьев Ф. и Г. Лондонов, В. Л. Гинзбурга и Л. Д. Ландау, а также Дж. Бардина, Л. Купера и Дж. Шриффера и других авторов) рассматриваются не временны^?е, а только пространственные (вне проводника) характеристики и их взаимосвязи, что не соответствует законам максвелловской электродинамической индукции токов. Поэтому в результате указанной фальсификации современные теории, так называемой "сверхпроводимости" не верны, что подтверждается их неспособностью давать количественные решения и рекомендации практического характера.

Кроме того, произвольно составляемые математические формулы (по существу математические модели) конкретных свойств и показателей "сверхпроводимости" электрического тока, обычно не проясняют, а только искажают представления о свойствах и их параметрических характеристиках.

Приведем наглядный пример. Уже в первой и основополагающей "теории сверхпроводимости" братьев Ф. и Г. Лондонов (1935 г.), постулируется [22] первое их (исходное) уравнение для плотности тока "сверхпроводимости" в виде:

0x01 graphic
,

где:

- вектор напряженности магнитного поля внутри "сверхпроводящего" образца,

? - глубина проникновения магнитного поля и электрического тока от поверхности "сверхпроводника",

- радиус-вектор точки образца относительно выбранной системы координат.

Второе уравнение Лондонов для магнитного поля в "сверхпроводнике" таково:

0x01 graphic
.

Приняв условия квантовой механики, Лондоны получили такую феноменологическую формулу для плотности тока "сверхпроводимости" в образце, находящихся в постоянном магнитном поле [9, стр. 98]:

0x01 graphic

0x01 graphic
,

где:

- функция, описывающая стационарное состояние коллектива электронов и зависящая не только от координаты r но и от A - вектор-потенциала магнитного поля;

- комплексно сопряженная функция;

- постоянная Планка;

i - мнимая единица;

q - заряд электрона;

m - инертная масса электрона;

?₀ - магнитная проницаемость материала;

? - оператор набла.

Функции

имеют свои не простые формулы.

Формула Лондонов составлена очевидно не для расчетов токов "сверхпроводимости", а для необычного оригинального пространственного представления автора о "сверхтоке". Для этого использованы, так называемые, "мнимая единица", "мнимые числа", "комплексные числа" с мнимыми компонентами и другие, например, "сопряженные комплексные числа", не существующие в реальности.

Принято, что мнимые числа имеют вид x = a + ib, где a и b действительные числа, а i = 0x01 graphic

(или i² = -1) есть мнимая, то есть воображаемая, единица. Равенствам для мнимой единицы не удовлетворяет ни одно действительное число. Здесь цифра -1 не есть отрицательное число как противоположное по смыслу действительной, вещественной единице, исчисляемой по условной шкале чисел. Два комплексных числа с мнимыми слагаемыми называются сопряженными (обозначаются как x и 0x01 graphic

), если у них действительные части равны, а мнимые отличаются знаком перед мнимыми числами. В таком случае считается, что сопряженные комплексные числа равны. Пример двух сопряженных комплексных чисел: x = a + ib и 0x01 graphic

= a - ib.

Из вышеизложенных положений теоретической алгебры следует, что наличие в формуле братьев Лондонов для тока "сверхпроводимости" мнимой единицы, следовательно, и мнимых чисел, а также некоторой комплексно сопряженной функции, делают саму эту формулу мнимой, то есть несоответствующей действительности как и ее мнимые компоненты не выражающие действительных численных значений их величин.

Спрашивается, анализируя приведенную выше формулу Лондонов, возможно ли понять что такое плотность "сверхтекучего" электрического тока и рассчитать его числовое значение, а также определить по формуле размерность тока 0x01 graphic

и оценить достоверность (безошибочность) получения этого сложного уравнения? Без ответов на эти вопросы формула Лондонов, и аналогичные формулы других авторов, не могут считаться правильными. Заметим, кстати, что, к сожалению, все существующие феноменологические "теории сверхпроводимости" описывают рассматриваемое явление подобными формулами, составленными без учета необходимой совместимости физических компонентов, без должностного обоснования необходимости введения их в формулу и математических операций с ними, еще и поэтому они не имеют реального физического смысла. Не случайно поэтому в отношении теории и уравнений Лондонов В.Л. Гинзбург писал: "Уравнения Лондонов не справедливы и в условиях нелокальной связи тока с полем", "Теория Лондонов приводит к неверным результатам при рассмотрении разрушения сверхпроводимости тонких пленок и при выполнении поверхностной энергии на границе между сверхпроводящей и нормальной фазами"; "Теория Лондонов непригодна в сильных полях Н, сравнимых с Н_с" и т. д. [31].

Критикуя "теорию сверхпроводимости" Лондонов, В.Л. Гинзбург и Л.Д. Ландау в своей "?-теории сверхпроводимости", как бы развивая теорию Лондонов, дают аналогичную основную формулу для тока "сверхпроводимости" в следующем виде:

0x01 graphic

где, как и в формуле Лондонов, i - мнимая единица, А - векторный потенциал поля, ? - оператор набла, е - заряд электрона, m - масса электрона, ? - параметр, характеризующий сверхпроводник, ?^* - истинная ?-функция электронов в металле, 0x01 graphic

- постоянная Планка, с - скорость света [31.С.128].

Очевидно, что критические замечания и претензии В.Л. Гинзбурга и Л.Д. Ландау к теории Лондонов и их основной формуле, а также наши сомнения в правильности использования мнимой единицы и мнимых чисел при бездоказательном написании формулы для тока "сверхпроводимости", которого как оказывается не существует в природе, всецело относятся к ?-теории Гинзбурга-Ландау и, в частности, к формуле для тока "сверхпроводимости". Следует отметить, что так называемая "?-теория сверхпроводимости Гинзбурга-Ландау" содержится в работах братьев Лондонов и, в частности, в их вышеприведенной формуле для тока "сверхпроводимости". Произвольное, необоснованное введение в формулы Лондонов (1935 г.) и Гинзбурга-Ландау (1950 г.) постоянной Планка

не превращает описываемую "сверхпроводимость" в квантовое явление аналогичное световому потоку. Если уже квантовать формулы данного явления, то по 2e, то есть по заряду куперовской пары электронов, а не по

Известно, что М. Планк в 1900 г. предположил, будто световое излучение телами происходит порциями - отдельными "квантами света" или "фотонами", энергия которых ?_ф связана с их частотой ? соотношением ?_ф =

??, где

= 6,62 ? 10^-14 Дж?с есть коэффициент пропорциональности, названный впоследствии "постоянной Планка". Но какое отношение имеет

света к явлению "сверхпроводимости" электричества? Ответ очевиден: никакого.

Распространение света (фотонов) и "сверхпроводимости" электрического тока ("сверхтекучесть" электронов) - это принципиально разные процессы. Считается, что в первом случае имеем движение фотонов вне их источника, то есть во внешней среде, а во втором - движение спаренных электронов внутри "сверхпроводника" без излучений света или иных излучений. Поэтому при математическом описании "сверхпроводимости" показатели светового потока

и c - скорость света вне вещества, не могут использоваться. У электрического, как и у света, большая, но своя, отличная от 300000 км/с, скорость распространения по проводнику. Следовательно, формулу Гинзбурга-Ландау для тока "сверхпроводимости" нельзя считать правильной.

Фактически все существующие феноменологические теории "сверхпроводимости" преемственны. Они только уточняют и развивают ошибочную теорию Лондонов. Следовательно, современная интегрированная теория "сверхпроводимости" содержит все те же принципиальные ошибки, противоречия, несоответствия экспериментам, то есть не является истинной даже в первом приближении к физической реальности.

С другой стороны все известные теории "сверхпроводимости", обычно основанные на взаимоиндукции соответствующих сверхтоков и полей, относятся только к случаю опытов с замкнутыми кольцами, в которых даже при допущении гипотетической индукции тока с очевидно одинаковым электрическим потенциалом (напряжением) во всем кольце, то току течь некуда, т. к. там нет перепада напряжения (давления), т. е. нет разницы электрического потенциала ?E. Опыты с прямым пропусканием электрического тока остаются вне рассмотрения "теоретической физикой сверхпроводимости". Нет приемлемой теории "сверхпроводимости" керамических материалов (диэлектриков). Туманно объясняются "сверхпроводниковые" туннельные эффекты в магнитных контактах Джозефсона. Нет ясности, почему обычно всепроникающее магнитное поле до наступления критической температуры легко заполняет весь объем тела, а при дальнейшем понижении температуры вдруг выталкивается из него и при этом тело становится диамагнитным и, следовательно, ток должен изменять свое направление. Почему, собственно, одиночные свободные электроны движутся в проводнике с сопротивлением, а в случае наступления диамагнитного ("сверхпроводимого", как считается) состояния вещества, его все еще свободные, но спаренные электроны моментально начинают двигаться в обратном направлении и без сопротивления?

Объяснения всех перечисленных выше и других кажущихся эффектов "сверхпроводимости" электрон-фононным взаимодействием спаренных электронов с атомами вещества неубедительны, ибо, во-первых, одиночные свободные электроны, очевидно, также взаимодействуют с атомами и у них тоже есть свое электрон-фононное взаимодействие, которое создает сопротивление движению; во-вторых, как это такое же взаимодействие спаренных электронов дает обратный магнитный эффект и уничтожает электросопротивление?; в-третьих, считается, что у "сверхпроводников"-диэлектриков свободных электронов нет, спариваться вроде бы нечему, а "сверхпроводимость" существует. Наконец, фононы - это что-то нематериальное, в отличие от электронов и атомов (ионов), а введены они в феноменологическую теорию "сверхпроводимости" для заполнения неизвестности. Подобных вопросов и противоречий в теории "сверхпроводимости" много, поэтому актуально и необходимо создать новую альтернативную, адекватную результатам экспериментов и непротиворечивую теорию уже "застарелого" (скоро 100 лет со дня открытия) явления, опубликованного Оннесом в 1911 году. Автор данной монографии, начиная с 1970-го года предлагает нетрадиционное представление, микроскопическую модель и основы магнитостатической теории рассматриваемого явления природы, ошибочно называемого сверхпроводимостью.

Опытами К. Мейсснера, А. К. Аркадьева и других установлено, что, во-первых, намагничивание веществ при закритически низких температурах происходит сильнее внешнего намагничивающего постоянного поля. Поэтому такое сверхсильное намагничивание (сверхсильное по сравнению с силой намагничивающего поля) мы называем сверхмагнетизмом. Во-вторых, было определено, что наведенное в теле сверхмагнитное поле всегда противоположно направлено по отношению к действующему на переохлажденное тело магнитному полю. Следовательно, вещества при низких криогенных температурах становятся сверхдиамагнетиками.

Переход обычно немагнитных веществ (например, свинца в опытах Оннеса, меди в известном эксперименте А. К. Аркадьева и различных керамических материалов), а также ферромагнетиков, парамагнетиков и слабых диамагнетиков в сверхдиамагнитное состояние есть по существу результат их фазового изменения третьего рода (III рода) - перехода веществ к сверхдианамагничиваемости.

3.7. О квантово-механическом объяснении явления

"сверхпроводимости"

Заметим сразу же, что ток "сверхпроводимости" - это, судя по экспериментам, должен быть постоянным электрическим током. Поэтому никакой квантуемости, порционной дискретности, периодичности и частоты как внутренних колебаний, так и электромагнитных излучений у тока "сверхпроводимости" (даже если это действительно ток) быть не может. Следовательно, известная квантовая теория физики неприменима для объяснения "сверхпроводимости". Но так как такие квантово-механические объяснения "сверхпроводимости" существуют и они признаются единственно правильными, то приходится их анализировать и делать соответствующие выводы.

Основоположник квантовой механики М. Планк в 1900 г. показал, что испускаемая телом энергия Е пропорциональна частоте ? волновых колебаний энергии в нем, то есть

0x01 graphic
,

где k - некоторый единичный квант (порция) энергии.

Для излучения электромагнитных волн эта зависимость имеет вид

0x01 graphic
,

где h = const = 6,62?10^-³⁴ Дж?с - постоянная Планка.

Постоянное значение h характеризует минимальную величину (квант) энергии электромагнитного излучения за один период изменения энергии атома в теле. Внутриатомные колебания не свободны и поэтому их частоты постоянны (? = const). Из этого следует, что для конкретного атома его внутренняя энергия может принимать кратные значения 1Е_А, 2Е_А,3Е_А...N Е_А. Поэтому излучаемая атомом энергия также будет дискретной, т.е. быть 1Е, 2Е, 3Е, ... NЕ. В этом истоки и суть квантовой механики микромира: атомов, молекул и связанных с ними процессов. Поэтому квантовая механика применима только к микроскопическим объектам и называется микроскопической теорией.

В случаях, когда частота колебаний ? ? const, то и Е ? const. К таким неквантованным колебаниям макроскопических процессов относятся различные колебания в больших, по сравнению с атомами, телах. Следовательно, квантовая механика неприменима при феноменологическом описании макроскопических (масштабных) процессов, таких как переменный электрический ток проводимости (так как у переменного тока частота может быть любой) и постоянный (без ?) ток "сверхпроводимости".

Как уже отмечалось, что многие ученые все же утверждают будто бы достоверное объяснение макроскопического явления "сверхпроводимости" можно дать только с позиций квантовой механики, которая, как общеизвестно, описывает объекты и явления микромира. Но так ли это? Рассмотрим этот вопрос подробнее. В общедоступной научной литературе ответ на поставленный вопрос дается умышленно запутанно посредством различных физико-математических ухищрений в виде допущений, введений, дополнений, условностей, ограничений и т.п., а также путем написания сложных уравнений с множеством произвольно вводимых математических операций. Поэтому в поисках вразумительного описания квантово-механической теории "сверхпроводимости" пришлось обратиться к учебникам физики для ВУЗов.

В современном учебнике по физике [39] в отношении квантовой теории "сверхпроводимости" на стр. 452 написано следующее.

Качественно явление сверхпроводимости с позиции квантовой теории объясняют так. Электроны проводимости в проводнике подвержены действию сил кулоновского отталкивания. Однако кулоновское отталкивание может быть ослаблено и даже исключено электрон-фононным взаимодействием. Положительные ионы решетки при определенных условиях, выполняя функцию посреднических элементов, могут привести в возникновению слабого взаимного притяжения между электронами. Электроны проводимости, притягиваясь друг к другу, образуют так называемую куперовскую пару. Энергия связи таких пар достигает 3,5 Т_к, то есть порядка ? 10^-³ эВ. Поэтому они могут существовать только при очень низких температурах. Электроны, составляющие куперовскую пару, имеют противоположные спины. И поэтому результирующий спин пары равен нулю, а пара по свойствам представляет собой бозе-частицу.

Куперовские пары концентрируются на низких энергетических уровнях. При сверхнизких температурах они находятся в одинаковом и достаточно устойчивом состоянии. Последнее обусловлено тем, что к бозе-частицам неприменим принцип запрета В. Паули, поэтому число куперовских пар, находящихся в одном состоянии, не ограничено.

Ансамбль куперовских пар может под действием внешнего электрического поля двигаться, не взаимодействуя с решеткой. Это значит, что пары при своем движении остаются невосприимчивыми к рассеянию и сохраняют движение даже после прекращения действия внешних сил, вызвавших это движение. Это и есть сверхпроводимость.

Возможно, что в приведенном выше кратком объяснении квантовой теории "сверхпроводимости" автору все понятно. Но все же есть много вопросов. Почему, например, к куперовской паре (она же бозе-частица) неприменим принцип запрета В.Паули и поэтому число куперовских пар, находящихся в одном состоянии, не ограничено? Куперовские пары создаются благодаря ионам. Электроны в паре притягиваются и удерживаются посредством положительно заряженного посредника - иона. В то же время множество куперовских пар может двигаться в теле почему-то не взаимодействуя с теми же ионами. Здесь явное противоречие. В данном объяснении "сверхпроводимости" "с позиций квантовой теории" физики о квантуемости электрического тока "сверхпроводимости" ничего не сообщается. Поэтому есть необходимость обратиться к другому более обстоятельному разъяснению квантовой теории "сверхпроводимости".

Рассмотрим квантово-механическую теорию "сверхпроводимости" изложенную в Курсе физики [40. С. 601-605], рекомендованном Министерством образования РФ в качестве учебного пособия для студентов высших технических учебных заведений.

Выписывая последовательными частями текст параграфа 42.3 "Сверхпроводимость" с основными положениями теории "сверхпроводимости" будем сразу же по мере приведения рассуждений авторов издания [40] сопровождать их своими вопросами, репликами и замечаниями заключенными в скобки и напечатанными курсивом. Это возможно облегчит понимание различий наших позиций относительно применимости квантовой теории к макроскопической "сверхпроводимости".

Читаем. Дж. Бардин, Л. Купер и Дж. Шриффер создали (1957) последовательную квантово-механическую теорию сверхпроводимости (теория БКШ). Выяснились не только физический смысл сверхпроводимости, но и основные ее особенности. Сверхпроводимость связана с особым (В чем особенность?) эффективным взаимодействием между электронами, которое происходит с участием кристаллической решетки и приводит (Как приводит? Почему?) к исчезновению удельного электрического сопротивления.

Рассмотрим подробнее характер этого взаимодействия. Электрон, движущийся в металле (Почему только в металле? "Сверхпроводимость" присуща и неметаллам.) при низких температурах, может (А может ли?) электрическими силами деформировать - поляризовать кристаллическую решетку (Поляризовать может, а деформировать нет, так как масса и заряд электрона намного меньше массы и заряда иона.). Наблюдается (?) некоторое смещение положительно заряженных ионов из их положения равновесия и некоторое изменение периодичности структуры решетки. Это существенно изменяет состояние электрона в такой решетке (Почему искажение и поляризация решетки изменяет состояние свободного от нее электрона?). Электрон оказывается окруженным "облаком" положительного заряда, притягивающегося к электрону. Величина этого положительного заряда превышает электронный заряд. Такой электрон вместе с окружающим его "облаком" имеет положительный заряд (Но это уже не электрон, и нечто другое.) и будет притягиваться (Или притягивается?) к другому электрону (Так образуется куперовская пара электронов?). При высоких температурах ничего этого происходить не может из-за теплового движения атомов (Чудеса, да и только. Но что такое электрический заряд гипотетического "облака"? Из чего состоит это "облако"? Каково его происхождение? Как у образовавшегося квазиэлектрона сочетаются отрицательный и положительный заряды? Почему обязательно положительный заряд должен быть больше отрицательного? Почему положительный заряд "облака" не есть свойство какой-либо иной микрочастицы вещества? Подобных вопросов возникает много, однако все они остаются без ответа в последующем изложении квантово-механической теории "сверхпроводимости").

Далее авторы анализируемого учебного пособия, основываясь на суждениях создателей современной теории "сверхпроводимости", утверждают, что притяжение электронов друг к другу не противоречит законам физики. Закон Кулона описывает взаимодействие зарядов в веществе формулой F_r= q₁q₂/4??₀?r². Если среда допускает, чтобы относительная диэлектрическая проницаемость была отрицательной (? < 0), то одноименные заряды будут притягиваться (Здесь авторы взаимодействие зарядов подменяют влиянием на них окружающей среды с различной диэлектрической проницаемостью, что ошибочно). Кристаллическая решетка сверхпроводника является средой, в которой относительная диэлектрическая проницаемость становится отрицательной и тем самым одноименные заряды притягиваются (Во-первых, диэлектрическая проницаемость среды или есть, или ее нет, то есть ? < 0 не бывает. Вообще, ничего меньше нуля, то есть меньше ничего, не бывает. Диэлектрическая проницаемость может быть равной нулю, то есть ? = 0, но в этом случае направленное движение (ток) электронов прекращается - электрический ток, в том числе и "сверхпроводящий" ток, невозможен. Во-вторых, как происходит смена ? > 0 при Т > Т_кр, на ? < 0 при Т © Т_кр? Очевидно, что при Т = Т_кр энергии направленного движения электронов проводимости не хватает преодолеть противодействие (сопротивление среды) и ток прекращается, при этом проницаемость тока ? = 0, а не ? < 0).

Авторы работы [40] написали, что межэлектронное притяжение в сверхпроводнике может быть качественно описано в понятиях и терминах квантовой теории. Далее дается такое описание явления "сверхпроводимости". Для простоты рассмотрим металл при 0 К. Движение электронов в кристалле, их столкновение с ионами решетки, нарушает нулевые колебания частиц решетки (Заметим, что нулевых колебаний не бывает) и переводит решетку в возбужденное состояние (При этом должна возрастать температура, но этого не происходит). Обратные переход решетки (Что вынуждает этот обратный переход?) сопровождается излучением энергии, которая поглощается электронами (Энергия поглощается единичными или уже спаренными, куперовскими, "сверхпроводящими" электронами?). Возбужденному состоянию кристаллической решетки соответствуют, как известно, кванты энергии звуковых частот - фононы (Вот откуда берутся кванты и фононы!). Поэтому процесс обмена энергией, о котором шла речь, рассматривается в квантовой теории как излучение фонона одним электроном, движущимся в решетке, и поглощение этого фонона другим электроном. Обмен электронов фононами приводит, при определенных условиях, к притяжению между электронами (Что за условия, при которых простой обмен электронов фононами приводит к их притяжению, преодолевая отталкивающую силу?).

Написано, что при низких температурах притяжение электронов в сверхпроводниках преобладает над отталкиванием электронов. Вся система электронов превращается в единый связанный коллектив. Энергетический спектр такой электронной системы уже не будет непрерывным (Почему? Наоборот становится взаимосвязанным и поэтому непрерывным). Возбужденное состояние (Что возбуждено? Электроны, решетка или вместе?) отделено от основного состояния некоторым интервалом энергии (Каким "интервалом" по величине?), некоторой энергетической "щелью". Квантовые переходы электронной системы не происходят при малых возбуждениях меньших ширины энергетической щели. А это означает, что вся энергетическая система движется без трения (Почему?), что свидетельствует об отсутствии электрического сопротивления (Тавтология какая то. Если квантовые переходы не происходят при малых возбуждениях, то для таких переходов энергии нужны возбуждения больше, чем ширина "щели", что должно увеличивать температуру и разрушать "сверхпроводимость". И как это в уплотненной решетке при очень низкой температуре система ли коллектив спаренных воедино электронов вдруг начинает двигаться без трения, без электросопротивления? Что является движущей силой "сверхтекучести" без трения огромного конгломерата двойных, спаренных воедино электронов, то есть в чем все-таки причина "сверхпроводимости" электрического тока? Пока что нет ответов на поставленные вопросы). Если же возбуждение электронной системы значительно, например, по сверхпроводнику пропущен ток, превышающий критический, то сверхпроводящее состояние разрушается (Значит, возбуждение должно быть и не маленьким и не большим. А каким?). Теория сверхпроводимости объяснила, почему хорошие проводники типа меди, серебра и т.д. не переходят в сверхпроводящее состояние даже при самых низких температурах (Как она это объяснила? Читаем далее это объяснение).

Хорошая проводимость связанная с малым удельным сопротивлением, является результатом слабого взаимодействия электроном с решеткой. Такое слабое взаимодействие не может вблизи температуры 0 К создать условия для возникновения межэлектронного притяжения, преодолевающего кулоновское отталкивание электронов. Поэтому сверхпроводящее состояние не возникает (Но заметим, что заряды электронов во всех металлах, и в неметаллах, равны. Взаимодействие электронов с ионами зависит от величины их зарядов. Следовательно, малое или большое электросопротивление зависит не от силы взаимодействия электронов с решеткой. Наиболее вероятно, что электросопротивление зависит от соотношения самоиндуцирующихся в проводнике магнитного и диамагнитного полей от проходящего по проводнику электрического тока - энергии электромагнитного поля). Межэлектронное притяжение, которое приводит к сверхпроводимости (Само по себе и как?), подчиняется определенным закономерностям. Важнейшей из них является то, что данный электрон неодинаково притягивается ко всем остальным, причем близость расположения не играет никакой роли (Почему так? Это же противоречит электрическим законам физики). Данным электроном будет выбран в качестве "партнера" в паре другой электрон, имеющий противоположный спин. Этот второй электрон может быть расположен от первого на расстоянии 10⁴ периодов решетки (Но это видимо уже не есть спаривание, а дальнодействие). И тем не менее взаимодействие этой пары наиболее сильное (Почему?). Поэтому весь сверхпроводник представляет собой единый связанный коллектив, который (Почему-то) не отдает энергию малыми порциями (Квантами) и движется без электрического сопротивления (Не взаимодействуя с положительно заряженной решеткой?). В сверхпроводниках наблюдается редчайший в физике пример дальней связи. Электронная система в сверхпроводнике представляется состоящей из связанных пар, которые называются куперовскими (по имени Купера, доказавшего, что слабое притяжение между электронами в металле приводит к их связанному состоянию). Возбуждение электронной системы сверхпроводника, переводящее сверхпроводник в обычный проводник, является результатом разрыва куперовских пар.

Авторы учебного пособия [40] полагают, что доказательством квантовой природы "сверхпроводимости" является "нестационарный эффект Джозефсона", когда при приложении к контакту Джозефсона постоянного электрического напряжения больше, чем его критическое значение для "сверхпроводников" контакта, то есть когда идет разрушение "сверхпроводимости", то в контакте возникает обычный электрический ток, пробивающийся через узкий зазор или тонкую пластинку из диэлектрического материала между двумя "сверхпроводниками". При этом естественно, что возникает падение напряжения U и контакт излучает определенные электромагнитные волны с частотой ?=2eU/ 0x01 graphic

. Это излучение обусловлено преодолением барьера электросопротивления. Частота ? связана с U, e и 0x01 graphic

, но предопределяется она внутренними особенностями (составом, структурой и т.п.) материалов контакта, от которых зависит электрическое электросопротивление и величина U. Следовательно, определенность и стабильность частот ? каждого конкретного контакта Джозефсона не является показателем и доказательством квантового характера проходящего по контакту электрического тока с сопротивлением. Тем более это излучение не имеет отношения к току "сверхпроводимости" даже если бы он там был и проходил без электросопротивления и уменьшения приложенного напряжения.

При этом авторы издания [40] настойчиво утверждают, что нестационарный эффект Джозефсона является экспериментальным доказательством наличия электронных пар в сверхпроводниках. Формула ?=2eU/ 0x01 graphic

написана под идею спаренных электронов в "сверхпроводнике". Но так как от постоянных величин 2е и 0x01 graphic

частота ? определенно мало зависит, а зависит от многофакторной величины U, то ни о какой макроскопической квантуемости тока "сверхпроводимости" говорить нельзя. Однако авторы все же утверждают, что нестационарный эффект Джозефсона впервые в истории физики экспериментально обнаружено, что макроскопическое явление - электрический ток - определяется микроскопической характеристикой - фазой волновой функции и квантуется, принимая лишь дискретные значения. При этом, по мнению авторов, "размываются" границы между макро- и микрофизикой. (Вопрос. Когда и где были обнаружены обязательно дискретные значения токов "сверхпроводимости"? Нет таких измерений).

Рассмотрим теперь то, что изложено в п.42.7 "Квантование магнитного потока [макроскопический квантовый эффект]".

Написано нижеследующее.

Одно из важнейших положений квантовой физики состоит в квантовании ряда физических величин (энергии, импульса и др.). Однако до недавнего времени предполагалось, что квантование происходит только в микромире и свойственно процессам в атомах, молекулах, атомных ядрах и т. п.... Изучение явлений, происходящих при температурах близких к 0 К, показало, что возможно макроскопическое квантование, то есть квантование величин, характеризующих макроскопические тела, размеры которых в 10³ раз больше атомных размеров. Вблизи 0 К оказывается возможным непосредственное наблюдение квантованных закономерностей (Интересно, какие это были наблюдения).

Опыт показывает, что ток в сверхпроводящем металлическом кольце становится незатухающим вследствие того, что ток в сверхпроводнике течет без сопротивления и потери на джоулеву теплоту отсутствуют. Однако с точки зрения классической физики отсутствие затухания тока в кольце остается необъяснимым (Как тут не среагировать на приведенное суждение. Если с точки зрения классической физики, то есть истинной, многократно подтвержденной физики, "сверхпроводящий" ток в кольце необъясним, то из этого следует, что эксперимент неправильно понят и в кольце нет и не может быть "сверхпроводящего тока электрической энергии, переносимой электронами). Движение электронов в кольце криволинейное и поэтому электроны должны терять энергию на излучение. Из-за этого ток даже в сверхпроводящем кольце должен затухать (Это правильно. Потеря энергии электронами на их искривление траектории не связано с электросопротивлением, обусловленным как считается взаимодействием электронов с ионами металла или с атомами иных тел. Следовательно, затухание тока в кольце в любом случае должно происходить. Но если это не происходит, то только потому, что в "сверхпроводящем" кольце нет тока, нет направленного движения электронов. Там есть нечто другое, а именно: кольцо в условиях эксперимента просто намагничивается).

Вот как "доказывается" макроскопическая квантуемость "сверхпроводящего" тока в кольце. Авторы [40] утверждают, что сверхпроводимость дает нам пример квантования макроскопической величины - силы тока. Сверхпроводящее кольцо позволяет наблюдать гигантский по масштабам квантовый эффект. Сила тока в сверхпроводящем кольце не принимает любые числовые значения и не изменяется непрерывно. Для всех электронов, движущихся в кольце, возникает гигантская боровская орбита и все квантовые закономерности, характеризующие ее в атоме водорода как бы переносятся на электроны в сверхпроводящем кольце (Во-первых, аналогия не считается доказательством. Во-вторых, никто пока что не измерил непосредственно силу тока в "сверхпроводящем" кольце. Поэтому утверждать, что в кольце течет ток, нельзя. Измеряли магнитное поле вблизи "сверхпроводящего" кольца и это означает, что кольцо намагничено. Более того, установлено, что у кольца нет электрического поля, что говорит об отсутствии в нем электрического тока).

Вероятно в качестве решающего довода, доказывающего макроквантуемость "сверхпроводимости", в книге [40] приводится следующий.

Квантование тока (Еще не доказано, что ток проводимости и "сверхпроводимости" квантуется) означает, что и индукция магнитного поля также квантуется и может принимать только ряд дискретных значений. Следовательно, будет квантоваться и магнитный поток ? сквозь площадь ?r² кольца. Другими словами ?=N?₀, где N=1, 2, 3,..., ?₀= 0x01 graphic

/2е=2,06785?10^-¹⁵Вб - некоторая порция магнитного потока (Заметим здесь, что числа N введены необоснованно, то есть как допущение, как предположение о квантуемости магнитного потока общего для всего кольца, находящегося в состоянии "сверхпроводимости". Однако на практике такой квантуемости больших магнитных потоков не наблюдается). Но все же, как пишут авторы, если радиус кольца r ? 10^-³ см, то при магнитном потоке ? = ?₀ магнитная индукция поля составляет порядка 1% от индукции магнитного поля Земли, то есть квант магнитного потока соответствует макроскопическому значению магнитной индукции. Экспериментально квант магнитного потока определен с весьма высокой степенью точности на основе эффекта Джозефсона (Сомнительно, что точно измерен квант магнитного потока "сверхпроводящего" в контакте Джозефсона. Но если измерили, то почему бы не привести конкретные данные этих измерений).

Аналогичный довод о квантуемости магнитного потока "сверхпроводника" спаренными электронами есть и в работе [17]. В ней В. Л. Гинзбург сообщает, что еще Ф. Лондон предполагал, что магнитный поток, проходящий через полый массивный сверхпроводящий цилиндр, отверстие или кольцо, должен квантоваться, причем квант потока ?₀=hc/e и поток ? = k?₀, где k - целое число и е - заряд частиц переносящих ток. Естественно, Лондон считал, что e = e₀ - заряд свободного электрона. Только в 1961 г. были проведены соответствующие опыты, показавшие, что фактически e = 2e₀. Таким образом,

0x01 graphic

(k = 0, 1, 2...).

Однако этот результат относится лишь к случаю массивных двухсвязных образцов, например, к полым цилиндрам, у которых толщина стенок значительно превосходит глубину проникновения магнитного поля в сверхпроводник [31. C. 63]. Из этого утверждения следует, что квантованность k потока ? есть результат прохождения "сверхтока" через специальные двухсвязные (джозефсоновские) и иные образцы сложной формы, а формула для ? не характеризует сам ток "сверхпроводимости".

Экспериментально обнаружить квантование магнитного потока, обусловленного предположительно квантованием тока "сверхпроводимости", очень сложно. Для того, чтобы измерить один квант потока (1?₀) необходимо, чтобы диаметр "сверхпроводящего" контура имел диаметр 10^-³см, а величина измерения не более 1Э. Реально это осуществлялось путем напыления свинца на кварцевую тонкую палочку диаметром 10 мкм. Такой образец переводили из нормального в "сверхпроводящее" (по существу в сверхдиамагнитное) состояние в различных магнитных полях и измеряли возникающий у образца магнитный поток. В опытах исследователи измеряли магнитный момент, связанный с "захваченным магнитным потоком". Квант потока определяли по величине вращательного момента, возникающего при воздействии на цилиндрический образец внешним магнитным полем. Испытываемый образец подвешивали на кварцевой нити. Измерялось отклонение образца по величине скручивания нити [114. C. 24]. И не понять то ли в эксперименте проявилось квантование с ?₀ или проявилось начальное (пороговое) сопротивление кварцевой нити скручиванию при многократном (ступенчатом) воздействии на образец разных по силе магнитных полей. С другой стороны, в данном эксперименте нет электрического тока вообще и "сверхпроводящего" в частности, а есть магнитное воздействие и намагничивание образца. Поэтому полученный результат ступенчатого отклонения образца при его намагничивании не имеет отношения к току "сверхпроводимости". Подобный результат можно получить и при комнатных температурах эксперимента.

Заканчивая дискуссионное рассмотрение вопроса о возможности создания квантовой теории "сверхпроводимости", необходимо обратить внимание на то, что были предприняты попытки применить положения квантовой физики микромира к макроскопическому процессу "сверхпроводимости" только металлов, так как в других материалах свободные электроны не предполагаются. Однако "сверхпроводимость" проявляется и у неметаллов: диэлектриков (изоляторов), полупроводников, биологических материалов и т. д., то есть "сверхпроводимость" свойственна любым материалам.

Если уж создавать макроскопическую квантовую теорию "сверхпроводимости", то она должна описывать не только металлы, но и всевозможные неметаллические материалы. Но пока объективных оснований для такой теории нет.

Очевидно, что "сверхпроводимость" по своей природе принципиально отличается от обычной проводимости электрического тока. Однако у названных "проводимостей" много общего. В частности, носителем электрической, магнитной и электромагнитной энергии является "полевая материя", а точнее - материя полей. Значит можно и нужно создать единую теорию проводимости и "сверхпроводимости". К сожалению, трудность состоит в том, что приверженность ученых установившимся представлениям об электронной проводимости и "сверхпроводимости" электрического тока не позволяют разобраться в фактах и создать соответствующие теории динамической проводимости тока и статической теории "сверхпроводимости", а по существу теории сверхдианамагничиваемости тел.

3.8. Представление о внутриатомном возникновении диамагнитного сопротивления веществ электромагнитному полю

Всякому действию есть противодействие. Поэтому немного ранее автором утверждалось, что электросопротивление (R) обусловлено электрической индукцией (D), то есть возникновением внутри токопроводящего тела контрэлектрического (D = -?E) и диамагнитного (B = -?H) полей индукции, направленных против электрического (E) и магнитного (H) полей, присущих току проводимости (J_пр) электрической энергии. Это научное положение основано на результатах экспериментов и на фундаментальной теории электричества Фарадея-Максвелла.

В основополагающем для теории электричества труде М. Фарадея "Экспериментальные исследования по электричеству" находим следующие суждения о природе электросопротивления: "Невозможно провести грань между явлениями изоляции и обыкновенной проводимости, если мы хотим заглянуть в самую их природу, т. е. в тот общий закон или законы, которыми определяется происхождение этих явлений... Сопротивление металлических проводов прохождению сквозь них электричества можно рассматривать как свойство изоляции. ...Но различные тела обладают этой способностью в большей или меньшей степени, что и делает их лучшими или худшими проводниками, худшими или лучшими изоляторами; по своей природе и действию индукция (изоляция - В.Ф.) и проводимость, по-видимому, одинаковы.

Из многочисленных общеизвестных примеров, доказывающих существование сопротивления в так называемых совершенных проводниках... Опыты были произведены в таком виде, чтобы доказать, что даже в случае металлов в условиях проводимости входит как элемент время. Когда разряд производился через медный провод ... и притом таким образом, что можно было наблюдать ... яркие искры на каждом из концов провода и его середине, то последняя заметно отставала во времени от первых двух, которые по условиям опята были одновременными. Вот доказательство запаздывания. ...Запаздывание обозначает изоляцию, а изоляция - индукцию" [103. С. 552-554].

Далее читаем: "Что же ... отделяет друг от друга сущность двух крайностей - совершенной проводимости и совершенной изоляции?". М. Фарадей так ответил на им же поставленный вопрос: "В природе мы не имеем совершенства ни в том, ни в другом конце, ни в смысле проводимости, ни в смысле изоляции". Из этого утверждения М. Фарадея следует, что в природе не может быть "сверхпроводимости" с нулевым электросопротивлением, т.е. без какой-либо по величине изоляции.

И еще: "...Первоначальное действие наэлектризованного тела на соседние тела заключается в приведении их частиц в поляризованное состояние, которое составляет изоляцию. ...Если индукция не ослабевает, то следствием является совершенная изоляция. ...Можно сказать, что изолятором являются те вещества, частицы которых могут удерживаться в поляризованном состоянии, а проводниками - те, частицы которых не могут оставаться устойчиво поляризованными" [103. С. 560-561].

Приведенные цитаты убеждают, что по данным Фарадея, природа изоляции, т. е. электросопротивления, состоит в самоиндукционной поляризации частиц материи, действие которых направленно против приложенного электрического поля и движения (тока) электрической энергии.

Поляризация материалов для электрического тока является важнейшим фактором. Считается, что поляризацию осуществляют диполи при их направленной структуризации под влиянием электрического и/или магнитного полей. При этом утверждается, что существуют в телах, соответственно, электрические и магнитные диполи.

Электрическим диполем называется система двух одинаковых по величине разноименных элементарных зарядов +q и -q, расстояние между которыми не велико и постоянно. Заметим, кстати, что, если между такими зарядами нет барьера, существование такого диполя невозможно, так как разноименные заряды притягиваются и их общий заряд q_1,2= 0.

Магнитный диполь представляется как элементарный заряд +q или -q движущийся по замкнутой (круговой) орбите [95. С. 28, 171]. Но и такой "диполь", как и электрический диполь, не может существовать самостоятельно, т.е. без того, что удерживает заряженную частицу на устойчивой, например, круговой орбите.

Простейшей устойчивой дипольной системой может быть только та, у которой между двумя отрицательно заряженными частицами, есть частица с двумя положительными зарядами. Расстояние между частицами микроскопическое. При этом орбиты более легких, имеющих отрицательные заряды, частиц электронов должны быть замкнутыми (круговыми или эллиптическими), находиться на одной оси и смещены относительно центральной положительно заряженной частицы (ядра). Эквивалентом структуры простейшего электромагнитного диполя является непланетарная модель атома гелия.

Диполи не существуют самостоятельно, то есть отдельно от их атомов вещества. Они являются структурными элементами (компонентами) любого атома. Очевидно поэтому, что у сложного атома диполей, по меньшей мере, столько, сколько пар электронов на внешнем электронном уровне не задействованных на связи с другими атомами тела.

Если такие электромагнитные диполи атомов тела расположены беспорядочно, то они создают его общее нейтральное состояние. Под влиянием внешней (постоянной или переменной) электромеханической силы (ЭМС) электроны и, следовательно, диполи активизируются, в теле возбуждаются, создается, по выражению М.Фарадея, "электротоническое состояние", то есть электрическое поле внутри и вне тела. В последствии при распространении, передачи энергии электрического поля по проводнику в нем, естественно, присутствует электрическое поле Е и, сопутствующее движению Е, то есть току J = ?Е, магнитное поле H, а так же противополе диамагнитной индукции B (противоположно направленное по отношению к H). Это следует из теории Фарадея-Максвелла и подтверждено практикой. Следовательно, сопротивление электрическому току создаётся не только тепловым движением атомов тела, но и в результате индукционной дианамагничиваемости (B) проводника от внешнего поля H электрического тока, а также внутриатомной самоиндукцией дополнительного диамагнитного поля ?B под влиянием индуцируемого диамагнитного поля B. Но как это может происходить?

Из теории электромагнетизма известно, что поляризация диполей той или иной направленности и их характеристики обусловлены в основном не орбитальными магнитными Р и механическими силовыми моментами L, а их спиновыми магнитными Р_s и механическими М_s моментами, для которых определено следующее соотношение:

0x01 graphic
,

где е - заряд электрона, m - масса электрона, а с - скорость света.

У единичного электрона спиновый механический момент минимален и равен [47. C.285]:

0x01 graphic
,

где

- постоянная Планка, квант энергии ( 0x01 graphic

=6,62?10^-²⁷ Эрг/с),

n = Ђ0, Ђ1, Ђ2, Ђ3, ... Ђi - главные квантовые числа.

Собственный, минимальный (при n = -1) спиновый магнитный момент электрона в атоме равен:

0x01 graphic
,

и его называют магнетоном Бора [95. С.313].

Величина P_s - 0,927?10^-23 Дж/Тл - 0,927?10^-2⁰ Эрг/Гс - 0,9273 ? 10^-20 Гс/см³.

Соотношение орбитального магнитного Р и орбитального механического L моментов электрона при естественных температурах есть величина постоянная и равна:

0x01 graphic
,

где v - скорость электрона на орбите, r - радиус орбиты.

Это соотношение в два раза меньше соотношения спиновых моментов. Из этого следует, что магнитные свойства веществ в большей мере предопределяются спиновыми магнитными моментами их атомов. Однако, и орбитальные магнитные моменты электронов также имеют существенное значение [47. С.285].

Доказано, что спиновый механический момент электрона М вдвое меньше его минимального (при n = 1) орбитального значения и равен 0x01 graphic

, а спиновый магнитный момент равен минимальному орбитальному моменту 0x01 graphic

, поэтому соотношения элементарных собственных моментов электрона таковы:

0x01 graphic

Действительно, спиновые магнитные характеристики электрона в два раза больше соответствующих орбитальных магнитных характеристик.

Под влиянием внешнего магнитного поля H показатели магнитных свойств электрона увеличиваются (в соответствии с квантово-механической теорией элементарных частиц вещества) кратно числам n = 1, 2, 3, ... i, то есть в 2, 3, 4 и более раза. Следовательно, увеличение P_s происходит на такие величины:

при n = 2 0x01 graphic

;

при n = 3

;

при n = 4

и т.д.

Следовательно, в действительности суммарно спиновый диамагнитный момент электрона в поле H:

P_s? = - (P_s+ ?P_s).

В таком случае соответствующая напряженность спинового диамагнитного поля B_s электрона в поле Н равна:

B_s? = - (B_s₀+ ?B_s),

здесь B₀ - собственное диамагнитное поле электрона (вне поля H), а ?B_s - дополнительно индуцированное спиновое диамагнитное поле электрона в атоме.

Исходим из того, что электроны в атомах изначально попарно взаимосвязаны, асинхронно движутся по своим равноудаленным круговым орбитам и имеют разнонаправленные вращения (разные спины: +1/2 и -1/2). При этом спиновые магнитные моменты (поля), будучи разнонаправленными, компенсируют друг друга. Так атом становится нейтральным. Под действием внешнего поля Н спаренные электроны поляризуются, они имеют одинаковый знак (приобретают одностороннее направление вращения), то есть приобретают однонаправленное вращение, а их спины одинаковые знаки +1/2 или -1/2. Так спаренные электроны атома переходят из нейтрального состояния в дипольное - становятся диполями.

Если вне поля Н суммарный спиновый магнитный момент спаренных в атоме электронов (диполя) равен нулю, то есть

0x01 graphic

то у диполя магнитный момент P_s_д вне поля Н таков

0x01 graphic

а под влиянием внешнего магнитного поля магнитный момент диполя равен

0x01 graphic

В случае синхронизации (совпадения) спинов при образовании диполя и его последующей поляризации поворота в поле Н, вклад спинового магнитного поля диполя в напряженность его диамагнитного поля B_s_H можно записать так:

B_s_H = В_s₁+ В_s₂ = (B₀₁+ ?B_s₁) + (B₀₂+ ?B_s₂) = 2B₀ + 2?B_s.

Приступая к анализу орбитального магнитного момента электрона, укажем, что он численно определяется известным уравнением [47. C.283]:

0x01 graphic

где: v - скорость движения электрона по орбите,

r - радиус орбиты,

? - частота вращения электрона по орбите.

Очевидно, что электрон в магнитном поле ускоряет свое движение по орбите: скорость v и частота орбитального вращения электрона ? увеличиваются. Считается, что при движении электрона по орбите под влиянием внешнего (стороннего) магнитного поля Н, его орбитальный магнитный момент равен произведению величины mr² на угловое ускорение d?/dt, то есть

Изменение частоты вращения электрона на орбите, при внесении его во внешнее магнитное поле Н таково [47. С.285]:

0x01 graphic

Поэтому количественно орбитальный магнитный момент электрона определяется уравнением [47. С.283]:

0x01 graphic

Следовательно, приращение орбитального магнитного момента электрона, индуцированное магнитным полем H, определяется по формуле [47. С.285]:

0x01 graphic

то есть это увеличение магнитного момента орбитального электрона в два раза больше магнитного момента электрона, будучи вне поля H.

Кроме того, можно с уверенностью считать, что уменьшение температуры тела Т способствует увеличению скорости внутриатомного движения электронов по своим орбитам. С понижением температуры скорость и, следовательно, частота вращения электронов ? увеличиваются. Эта температурная зависимость приводит к дополнительному увеличению диамагнитного поля электронного диполя на величину

0x01 graphic

где k - некоторый коэффициент, зависящий от положения электрона в структуре атома, от его электронного уровня.

Учитывая магнитный и температурный эффекты, суммарный орбитальный магнитный момент электрона можно записать в виде:

0x01 graphic

или

0x01 graphic

Переходя от магнитных моментов к магнитному полю электрона, в частности, к диамагнитному полю внутриатомного электрона, находящегося в поле H и при температуре Т, можно записать, что численно

В_0? = В₀ + ?В₀_H + ?В₀_T.

У диполя, состоящего из двух электронов, эти показатели удваиваются.

В итоге, диамагнитное поле диполя B_д_._д в поле H при определенной температуре Т состоит из суммы вышеприведенных составляющих

B_д_._д = В_S? + В_O? = В_S₀ + ?В_S + В_O + ?В_O_H + ?В_O_T =

= В_S? + В_O? + ??P_i.

Переходя от диполя к поляризованному атому, мы должны учесть спиновые и орбитальные магнитные моменты всех электронных диполей. Полный диамагнитный момент атома таков:

P_ат = 0x01 graphic
P_д._д_n = -B_ат,

где: n - количество магнитных диполей в атоме.

В отсутствии поля H в атоме не возникают диполи, и поэтому P_ат = 0 и B_ат = 0.

Диамагнитный момент (сила диамагнитного поля B), возникающий в веществе под влиянием поля H, зависит от числа атомов N в теле и может быть рассчитан по простой формуле:

P_в-ва = NP_ат = ? H.

Коэффициент ? называется магнитной восприимчивостью вещества. Реальные значения ? всегда больше нуля.

Величина диамагнитного поля рассчитывается по формуле:

0x01 graphic

У различных веществ магнитная восприимчивость (как и проницаемость) существенно различаются. Так, например, у меди диамагнитная восприимчивость равна 0,9 · 10^-5, а у "сверхпроводников" этот показатель, по расчетным данным В.Л. Гинзбурга, может достигать значений до 3,18 · 10⁹.

Рассмотрим вопрос о том, какова намагничиваемость M, то есть каково итоговое магнитное поле тела, находящегося в поле H.

Известна зависимость поля B, индуцированного полем H. Она такова:

0x01 graphic
или

Поля B и H противоположно направлены. Следовательно, магнитное поле тела M есть разница напряженностей полей H и B, то есть

0x01 graphic
.

Если H > B, то это парамагнетик; если H >> B то это ферромагнетик; при H < B - диамагнетик, а состояние при H << B характеризует сверхдианамагниченность тела и его неспособность передавать (проводить) электрический ток с магнитным полем Н. Эту же закономерность записывают и так: вещества с положительной магнитной восприимчивостью ? > 0 есть парамагнетики и ферромагнетики, а вещества с отрицательной (в смысле противоположно направленной) магнитной восприимчивостью

? диамагнетики (полупроводники и слабые диэлектрики) и, добавим, сверхдиамагнетики (изоляторы).

Из вышеизложенного взаимодействия внутренних (собственных) полей тела, находящегося во внешнем магнитном поле Н от любого по происхождению источника, следует, что течению электрической энергии (электрическому току J_пр=?Е с его магнитным полем Н) противодействует индуцируемое в любом теле диамагнитное поле В. Следовательно, проводимость ? и электросопротивление R (или ?) есть в основном диамагнитная реакция вещества на внешнее магнитное поле Н.

В случае сверхдианамагниченности тела (при низких температурах) диамагнитное поле B >> H, электросопротивления нет, так как нет электрического тока. При этом сверхдианамагниченный, а не "сверхпроводящий", материал становится сильным диэлектриком (изолятором), что подтверждается результатом анализа научных данных, получаемых при соответствующих экспериментах.

Для более полного представления процесса сверхнамагничивания тела от внешнего поля Н, необходимо учесть спонтанную и вынужденную поляризацию диполей вещества и лавинообразное [32] (подобно "цепной реакции") увеличение диамагнитного поля самоиндукции (В > Н).

Под действием стороннего магнитного поля Н (в составе электрического тока или самостоятельного) в материале возникают два противоположно направленных магнитных поля:

1) H?- внутреннее поле совпадающее по направлению и примерно равное внешнему полю Н;

2) В - диамагнитное поле самоиндукции как реакция тела против поля Н.

Вероятно, что соответствует реальности и такое рассуждение. Если в теле (в проводнике с электрическим током или без него) преобладает собственное поле H?= H, то оно вызывает некоторое дополнительное поле ?H? от спонтанной поляризации большего числа диполей в направлении и под влиянием собственного поля H?. Это происходит если H? > В. В другом случае, когда В > H? в теле индуцируется дополнительная напряженность поля ?B однонаправленного с полем В.

Следовательно, общее магнитное поле М, при H? > В, можно записать в виде:

0x01 graphic
,

а при условии В > H?

0x01 graphic
.

Выражение М₁ справедливо для ферромагнетиков и парамагнетиков, а М₂ для диамагнетиков и сверхдиамагнетиков.

Сумму H?+? H? обозначим буквой Н, а В+?В буквой B. Тогда

М₁= Н - В, а М₂= -(B - Н) .

По намагничиваемости все вещественные тела можно разделить на следующие четыре группы:

1. Вещества, у которых поле В намного меньше поля Н называются ферромагнетиками, а по существу они сверхпарамагнетики с общим магнитным полем

М_ф= Н - В .

2. Вещества, у которых индукция собственного диамагнитного поля В велика, но меньше Н, то такие вещества называются парамагнетиками. Их магнитное поле

М_П= Н - В и М_П<< М_Ф.

3. Вещества, у которых индукция собственного магнитного поля B =В+?В велика, но немного больше Н, называются диамагнетиками. Суммарное магнитное поле в таком случае таково:

М_Д = - (B - Н) .

4. Вещества, у которых индукция собственного магнитного поля B намного больше поля Н, а намагничивание осуществлено при закритически низкой температуре, то имеем сверхдиамагнетик с общим магнитным полем

М_С = - (B - Н) и М_С>>>М_Д

Магнитные свойства веществ взаимосвязаны с их электрическими свойствами. Ниже приведены усредненные показатели некоторых свойств магнетиков, в частности, магнитной восприимчивости ?, магнитной проницаемости 0x01 graphic

и удельного электросопротивления ?:

- ферромагнетики ? ? > 0, ? > 1, ? = 10^-6- 10^-8Ом?м;

- парамагнетики ? ? > 0, ? ™ 1, ? = 10^-5- 10⁸Ом?м;

- сверхдиамагнетики ? ? > 0, ? < 1, ? > 10²⁰Ом?м.

В итоге показатели намагничиваемости, магнитной восприимчивости, магнитной проницаемости и электросопротивления различных типов веществ можно сопоставить и получаем:

М_Ф >> М_П, а М_Д <<< -М_С ,

?_Ф << ?_П, а ?_Д <<< ?_С ,

?_Ф > ?_П, а ?_Д < ?_С .

Из этого сопоставления показателей свойств видно, что, во-первых, они действительно взаимосвязаны и, во-вторых, так как М регламентируется магнитной индукцией противополя В или B, то, следовательно, все магнитные и электрические свойства, в частности проводника с током, есть результат суперпозиции (наложения) магнитного поля Н или Н и диамагнитного поля самоиндукции В или B. В этом физическая природа сопротивления тел распространению по ним как электрического тока (электромагнитной энергии), так и магнитного потока Ф.

Если при пропускании электрического тока В < Н, то тело является электропроводником, а если B ™ Н, то такое тело есть диэлектрик (изолятор).

3.9. К вопросу о макроскопической теории электрического сопротивления проводников и изоляторов

Как уже отмечалось, Оннес глубоко ошибся в том, что он, вначале исчезновение разности электрических потенциалов, а позднее возникновение у металлических проводов усиленной намагниченности, счел за исчезновение электросопротивления и переход исследованных металлов в стояние сверхпроводимости существенно большего электрического тока, чем при обычных (естественных) температурах.

Дело в том, что Оннес, как и большинство ученых, придерживался упрощенного представления об электрическом токе как о движении заряженных частиц (в частности, свободных электронов) внутри металлических материалов и в других средах под действием электрического поля. Поэтому считается, что сопротивление электрическому току есть противодействие, которое оказывает проводник движущимся в нем электрически заряженным частицам. Однако давно существует другое понимание что такое электрический ток и сопротивление ему. В этом случае природу электрического тока представляют как передачу электромагнитной энергии не движущимися частицами вещества, не корпускулами, а полевой (бесструктурной) материей. То есть электрический ток - это движение электромагнитного поля с его электрической и магнитной составляющими. Следовательно, физическая природа электрического тока, хоть и связана с зарядами электронов, все же не является вполне корпускулярной; она по сути полевая. Поэтому в электросопротивлении, кроме тепловой (температурной) компоненты, есть также полевые, то есть диэлектрический и диамагнитный компоненты. Эти научные положения основаны на результатах экспериментов Фарадея [103] и на фундаментальной теории электричества Максвелла [71].

Эксперименты и теория с очевидностью доказывают, что распространение (ток) скрытой электрической энергией происходит посредством образования в проводнике электромагнитных диполей и их поляризации в направлении действия электрического Е и магнитного H поле, образуя суммарное однонаправленное электромагнитное поле S. Движение этого электромагнитного поля и есть электрический ток I, то есть происходит передача по проводнику потенциальной электродвижущей энергии поля S. Следовательно, I = G ? S, тогда как по закону Ома I = G ? E.

Кроме того известно, что при электрическом токе в проводнике индуцируется (возникает) противополе электрической индукции D ("виртуальный ток смещения") и диамагнитное (то есть противоположно направленное по отношению к Н) поле В. В проводнике с током одновременно существуют Е, Н (S) и D c B. Очевидно, что сопротивление электрическому току создают в основном поля D и B, а также тепловое хаотическое движение атомов (температура).

В подтверждение вышеизложенному укажем на то, что в математической теории Максвелла, формализующей содержательную (смысловую и фактическую) теорию электричества Фарадея, все уравнения содержат только характеристики соответствующих полей. Не случайно и основные (итоговые) уравнения Максвелла в векторном выражении называют уравнениями полей электродинамики. Соответствующие скалярные уравнения теории электричества тоже полевые о чем свидетельствуют их формулы:

I_пр= G ? E, D = ? ? E, и B = ? ? H,

где I_пр - плотность электрического тока проводимости,

E - полевая напряженность электрического тока,

D - электрическая индукция,

B - магнитная индукция (H>B у проводников, B>H у обычных изоляторов, B >> H у "сверхпроводников", т.е. у суперизоляторов),

G - электропроводность,

? - диэлектрическая проницаемость,

?_м - магнитная проницаемость.

Из приведенных соотношений следует, что условия электропроводимости таковы:

Если ? < 1 и ?_м> 1, тогда E > |-D|, H > |-B| и I_пр> 0.

При ? ™ 1 и ?_м™ 1 получаем:

|-D| ™ E, |-B|™H и I_пр= 0,

Это означает, что материал при таких показателях является слабым изолятором.

При ? >> 1 и при диамагнитной проницаемости ?_д>> 1 материал обладает высоким диамагнетизмом; он абсолютный диэлектрик (идеальный изолятор) с I ? 0.

Вопрос сопротивления электрическому току обычно рассматривается исходя из закона Ома. Согласно этому закону сила тока (количество электричества) I в проводнике прямо пропорциональна разности потенциалов на концах проводника, которую иногда называют "напряжением на сопротивлении", "падением напряжения" или "напряжением между измеряемыми точками проводника", и обратно пропорциональна сопротивлению.

где ?_н и ?_к - значения потенциалов у начала и конца рассматриваемого участка проводника, R - сопротивление этого участка, U_нк - электрическое напряжение на данном участке проводника.

Следовательно,

а величина обратная сопротивлению, то есть

называется проводимостью электричества.

Единицей проводимости в системе СИ служит сименс (См), а единицей наименьшего сопротивления принят один Ом (1 Ом). Один Ом - это сопротивление проводника, по которому течет ток в один ампер (1 A) при напряжении U_ab в один вольт (1 В). Поэтому показатель проводимости G имеет следующие значения:

При G = 0, когда R = ?, проводимости нет, следовательно, материал является абсолютным диэлектриком, идеальным изолятором. При R = 1 Ом и G = 1 имеем наибольшую проводимость. Значений G > 1, тем более вплоть до R = ?, то есть "сверхпроводимости", не может быть как по физическим причинам, так и по условиям математики, ибо любое число разделить на единицу и, в частности, на величину меньше единицы (на R < 1) нет возможности. При попытках сделать такое ошибочное "деление" на число меньше единицы фактически осуществляется умножение на знаменатель дробного делителя, что противоречит арифметическому делению, а также физическому представлению о проводимости электричества. Деление на R < 1 также делает бессмысленной и противоречивой формулу закона Ома, так как в таком случае вместо уменьшения делением значения тока I получается его увеличение, то есть умножение. В результате такого "деления" сторонники идеи "сверхпроводимости" утверждают, что в "сверхпроводящем проводнике течет необыкновенно, почти бесконечно большой ток" и что "по очень тонкому сверхпроводнику можно передавать практически бесконечно большие токи и без сопротивления". Но эти невероятные суждения ещё никто не подтвердил и вряд ли подтвердит экспериментально.

С другой стороны, учитывая, что Оннес измерял разность потенциалов ?_н- ?_к = U_нк на отдельном участке электрической цепи из замороженной ртути и получал при 4,2К U_нк = 0, то, подставляя это значение в числители соответствующих физических формул для тока и электросопротивления, Оннес должен был получить значения I и R равными нулю. Это свидетельствует, что при U_нк = 0 в "сверхпроводнике" тока нет, так как материал становится диэлектриком (изолятором), а не "сверхпроводником". Однако Оннес почему-то сделал совершенно противоположные умозаключения, которые, к сожалению, до сих пор признаются правильными.

Повторяем непонятно как и почему Оннес оценивал электросопротивление по разности электрических потенциалов на концах исследуемой проволоки, т.е. по ?_н - ?_к = U, где ?_н и ?_к электрические потенциалы начала и конца проводника, а U - электрическое напряжение на данном участке проволоки.

По закону Ома ток

Следовательно, если разность потенциалов уменьшается из-за уменьшения ?_н, то и ток уменьшается. При постоянстве ?_н и уменьшении ?_к, т.е. при увеличении ??, ток тоже уменьшается. Следовательно, снижение ?? = ?_н- ?_к всегда ведет к уменьшению силы (или плотности) тока. При ?? = const, величина R тоже неизменна и I = const. При изменении величины ?R пропорционально изменяется ?? и наоборот. Показатели U и R - это взаимозависимые величины, так как

0x08 graphic

При ?? = 0, как при "сверхпроводимости", ток I = 0/R = 0. Это же очевидно

Если считать, что сопротивление R пропорционально ?? на данном участке проводника, то получаем:

При ?? = 0 ток I и сопротивление R всегда равны нулю.

Следовательно, при условии ?? = 0 не может быть ни обычного, ни "сверхпроводящего" тока.

Считается, что электросопротивление обусловлено тепловым движением атомов проводника. При возрастании температуры повышаются тепловые колебания атомов проводника и увеличиваются столкновения электронов (носителей зарядов) с атомами, что препятствует движению электронов и этим повышает сопротивление электрическому току. Снижение температуры, наоборот, уменьшает амплитуду колебаний атомов и, следовательно, уменьшает количество столкновений электронов с атомами, потери энергии электронов уменьшаются, сопротивление проводника движению в нем электронов также уменьшается.

Предполагается, что при абсолютном нуле температуры атомная структура вещества неподвижна, и электросопротивление такого идеального проводника должно быть равным нулю. Исходя из этих предположений и опытов по "сверхпроводимости", был сделан ошибочный вывод: "сверхпроводящие" материалы являются идеальными проводниками с R = 0. Позднее под давлением фактов этот вывод-предположение был опровергнут, да он и изначально-то был неправдоподобным, так как движущиеся электроны не могут абсолютно не взаимодействовать даже с неподвижными атомами, а увеличивающаяся при охлаждении плотность атомов (и без того плотноупакованной кристаллической решетки, например, металлического проводника) должна увеличивать электросопротивление. Поэтому любой проводник не идеален, так как в нем движущиеся электроны непременно должны сталкиваться с атомами проводника даже при абсолютно нулевой температуре. Поэтому электросопротивление не может быть меньше некоторого минимального значения, что было подтверждено Оннесом при исследовании электрических свойств платины при сверхнизких температурах. Это схематично показано на рис.5, кривая 2.

Известно, что у некоторых металлов наблюдалось увеличение электросопротивления при очень низких температурах. Это объясняется предполагаемой низкотемпературной конденсацией свободных электронов на атомы, вследствие чего проводимость (количество проводимого электричества), определяемая числом свободных электронов в теле, уменьшается, а электросопротивление увеличивается (рис.5, кривая 3). Так как при температуре 0К вероятно все свободные электроны конденсируются и закрепляются в атомах, то электросопротивление должно стремиться к бесконечности (R ? ?), а не к нулю, как это утверждают многие авторы публикаций о "сверхпроводимости".

Легко убедиться, что увеличение электросопротивления при приближении температуры к 0 К не может быть объяснено в рамках существующей электронной теории электрического тока.

Спрашивается, почему и как, при температуре ниже критической, внезапно прекращаются соударения движущихся электронов с атомами (ионами) проводника, исчезает их тормозящее взаимодействие, и появляется энергетически незатратная "сверхпроводимость"? Современная теория мнимой "сверхпроводимости" объясняет это кажущееся явление спариванием электронов, что ухудшает их проводимость, а также каким-то особым "электрон-фононным взаимодействием" спаренных электронов с положительно заряженными ионами внутри тела. При наличии электрон-фононного взаимодействия в проводнике должно быть сопротивление электрическому току, что отрицает "сверхпроводимость". Следовательно, электронная теория "сверхпроводимости" не согласуется с указанными фактами и с её же суждениями о природе перехода проводника с R > 0 в "сверхпроводящее" состояние с R = 0.

Объяснение Оннесом и другими учеными эффекта увеличения электросопротивления при супернизких температурах "примораживанием" электронов к атомам сомнительно и ничем не подтверждается. Исчезновение электросопротивления при таких же низких температурах объясняется тем, что проводящие электроны становятся несвязанными, и факторы, мешающие их движению, как-то исчезают. Такие объяснения Оннеса не представляются убедительными, достоверными и не могут быть истинными.

Дело в том, что физическая природа электрического потенциала, проводимости (тока) электрической энергии и сопротивления электрическому току со стороны материала состоит в другом. Существующая микроскопическая теория электричества, основанная на идее свободных электронов в электропроводящих материалах, не соответствует многим фактам и поэтому не может признаваться достоверной.

В отношении электросопротивления можно утверждать, что оно происходит от двух причин: от температуры, а точнее от теплового колебания атомов, которое разрушает поток электромагнитной энергии, передаваемой электромагнитными диполями вещества, а также от деполяризации этих диполей и контрполяризации их противоположно действующему магнитному полю электрического тока, то есть от действия индуцированного током диамагнитного поля В.

Признавая, что тепловое электросопротивление тел (R_T) тем сильнее, чем больше температура проводника. При этом диамагнитное холодное сопротивление (R_В) проводника с током существенно возрастает при уменьшении его температуры. Следовательно, противоположная зависимость этих двух видов (причин) сопротивлений на суммарное электросопротивление проводника (R) можно представить в виде графиков рисунка 10. На этом рисунке показано формирование зависимости 1 как суммы R_T и R_B.

Рис.10. Схема влияния температурного (R_T) и диамагнитного (R_B) сопротивлений на суммарное электросопротивление R проводника при различных температурах

Если кривая зависимости диамагнитного электросопротивления какого-либо материала выше и круче, чем кривая 2 рисунка 3, то суммарное электросопротивление не уменьшается с понижением температуры, а увеличивается. Такими материалами, с отрицательной температурной зависимостью электросопротивления, являются, в частности, полупроводники. В этом случае становится понятным, почему их критическая температура перехода в сверхдиамагнитное и супердиэлектрическое (а не в "сверхпроводящее") состояние Т_кр существенно выше, чем у обычных проводников. Это объясняется тем, что у полупроводников, и у других керамических материалов, B и R_B часто намного больше H и R_T. Поэтому эти материалы, называемые сейчас "сверхпроводниками второго рода", являются лучшими сверхдиамагнетиками и изоляторами (а не сверхпроводниками), чем хорошие металлические проводники (правило Матиаса). По Матиасу странно, что "хорошие проводники являются плохими сверхпроводниками". Однако, учитывая величины и обратную зависимость значений B и R_B от T, становится понятно, почему хорошие проводники, при их глубоком охлаждении труднее сверхдианамагничиваются и превращаются в хорошие изоляторы.

Впредь, рассматривая вопрос о "сверхпроводимости", надо помнить, что разность потенциалов не однозначно соответствует электросопротивлению. Параметр ?? = ?_н- ?_к тем меньше, чем больше значение диамагнитного поля В в проводнике. Под увеличенным влиянием противополя В уменьшается ?_ни, следовательно, ?_к. Это общее падение потенциалов на входе и выходе тока из участка проводника соответствует уменьшению силы (плотности, количеству) тока I. Очевидно, что при условии B ™ H разность электрических потенциалов ?? = 0 и поэтому I = 0.

Исчезновение разности потенциалов в экспериментах Оннеса, то есть отсутствие в образце электрического поля Е, и появление усиленного диамагнитного поля В, взамен магнитного поля Н от электрического тока, доказывают, что металлические материалы при температурах ниже критической становятся диамагнетиками и диэлектриками (изоляторами), а не сверхпроводниками, как это ошибочно утверждал Оннес. К сожалению, это неправильное и противоречащее многим фактам суждение Оннеса разделяют ученые до сих пор, что трудно понять и объяснить.

Об отсутствии электрического тока в "сверхпроводниках" свидетельствуют исследования по оценке величины их диэлектрической проницаемости. Так, например, в работе А.А.Абрикосова читаем, что "сверхпроводящий ток, согласно теории Лондона, приводит к появлению диэлектрической проницаемости... Кроме того, Л.Д.Ландау высказал предположение, что электроны в сверхпроводнике могут давать большую диэлектрическую проницаемость ?₀, ... имеющую порядок величины 10⁸ - 10¹⁰ при Т << Т_к" [1.С.43]. М.Я.Азбель в статье "Об определении диэлектрической постоянной сверхпроводников" указал, что в работе [1] были получены формулы определения диэлектрической постоянной сверхпроводников с учетом её аномально высокой величины" [3.С.705]. В.Л.Гинзбург в работе "Современное состояние теории сверхпроводимости" [28] обосновывал, что диэлектрическая постоянная (проницаемость) ?₀ в сверхпроводящем состоянии, не связанная с током j_s, может быть весьма высока. Расчеты В.Л.Гинзбурга показали, что общая диэлектрическая проницаемость ? сверхпроводника может иметь значение порядка -3,18 ? 10⁹ [28.С.338]. В другом месте этой же работы В.Л.Гинзубрга написано: "При низкой температуре (Т ? 0) ... нормальная проводимость G в сверхпроводнике стремится к нулю. Таким образом, свободные электроны, не переходящие в сверхпроводящее состояние, не могут остаться свободными. ... Следовательно, при переходе в сверхпроводящее состояние часть свободных электронов металла, около 10% при Т ? 0, начинает участвовать в сверхпроводимости, остальные 90% электронов "замерзают", т.е. переходят в связанное состояние... Поэтому "замерзшие" электроны должны внести заметный вклад в значение ?, а именно ... вклад порядка 10⁸ ¤ 10¹⁰" [28.С.345]. Такое резкое увеличение показателя диэлектрической проницаемости проводника при Т ? 0 безусловно должно вести к прекращению электрического тока, а не к его "сверхпроводимости", даже если бы какая-то часть электронов оставалась сверхпроводящей, что невозможно.

Итак, из опытов Оннеса и его последователей объективно следует, что при Т ? 0 материалы, в частности металлы, переходят из состояния проводящего электричество в диэлектрическое состояние, обусловленное относительно устойчивым сверхдианамагничиванием вещества [см.109]. Это явление перехода переохлажденного, графитового проводника электрического тока в состоянии изолятора, то есть в состояние сверхдиэлектрика, а не "сверхпроводника" как ожидалось, убедительно доказано в работа [127] и [128].

4. ВВЕДЕНИЕ В СУБМИКРОСКОПИЧЕСКУЮ (ВНУТРИАТОМНУЮ) ТЕОРИЮ СВЕРХДИАМАГНЕТИЗМА

4.1. Анализ планетарной модели атома

Можно согласиться с автором работы [123], сделавшим выводы, что, с одной стороны, "важнейшим препятствием, чрезвычайно затруднившим процесс исследований сверхпроводимости, явилось то, что образно говоря, природа необычайно искусно "загримировала" сверхпроводимость под фактически не имеющую с ней ничего общего, идеальную проводимость", и, с другой стороны, "...проблема сверхпроводимости тормозила прогресс электронной теории металлов и, наоборот, стимулировала разработку теории фазовых переходов II рода" [69. С. 9]. Очевидно, что надо рассматривать явление сверхнамагничиваемости тел при фазовом переходе особого рода в условиях температуры Т © Т_кр с позиций новых и более реалистичных моделей и теорий электронного строения атомов и их связей в твердых телах.

В 1896 г. Лоренц изложил свое представление об электронах, входящих в состав атомов. По мнению Лоренца, атом представляет собой систему электрических зарядов (электронов и ионов), которые под действием электромагнитных волн совершают колебательные движения с определенной частотой. Исследованиями поглощения света атомами установлено, что частота видимого света составляет 10¹⁴-10¹⁵ колебаний в секунду. С такой частотой могут колебаться только частицы малой массы - электроны. Электроны внутри атома, по Лоренцу, имеют упругие взаимосвязи. Электронная теория атомного строения атомов Лоренца объясняет многие явления, связанные с распространением и поглощением света в веществе.

В начале XX столетия Д. Д. Томсон предложил уточненную модель атома. Томсон считал, что положительный заряд атома непрерывно распределен в пределах сферы, размеры которой определяют размер атома. Внутри этой сферы электроны распределены симметрично.

Вскоре опытами Э.Резерфорда по рассеиванию атомами ?-частиц было доказано, что представление об обобщенном положительном заряде, предложенное Томсоном, не соответствует действительности. Согласно модели атома, предложенной Резерфордом, весь положительный заряд и почти вся масса атома сосредоточена в центральной части атома - в атомном ядре с диаметром порядка 10^-13 см. Атом, по Резерфорду, подобен солнечной системе (солнце - ядро, планеты - электроны). Эта модель представляла атом как динамическую систему движущихся электронов вокруг положительно заряженного ядра. Но модель Резерфорда тоже оказалась неудовлетворительной.

Дело в том, что электроны могут двигаться вокруг ядра по траекториям, являющимся кривыми второго порядка, т. е. по окружности или по эллипсу. Но такое обращение электронов вблизи ядра не может быть устойчивым, оно (по расчетам ученых) должно сопровождаться излучением (затратой) энергии, и в результате электроны обязаны упасть на ядро и атом прекратить свое существование за доли секунда. Однако этого не происходит. Атомы в устойчивом состоянии существуют, вероятно, миллиарды лет.

По планетарной модели все электроны, будучи равными по массе и заряду, должны были бы двигаться во всех атомах по одной орбите, а не на разных пространственно-энергетических уровнях, как это следует из экспериментов по определению спектров излучений энергии предварительно возбужденных атомов. Дискретные спектры длин волн излучений атомов доказывают, что орбиты электронов в атомах неодинаковы.

Модуль Резерфорда уточнил Н. Бор двумя постулатами.

1. Постулат о стационарности состояний: атомы, несмотря на происходящие в них движения электронов, не излучают энергию; атомы обладают дискретным рядом энергий; переход электронов с одного энергетического уровня на другой происходит скачком.

2. Условие перехода атома из одного состояния в другое: при переходе из одного стационарного состояния в другое атомы испускают или поглощают энергию строго определенной частоты.

Следующим шагом в развитии планетарной модели электронных оболочек атомов было доказательство того, что электроны, как и другие микрочастицы, обладают не только корпускулярными, но и волновыми свойствами. Это означает, что вокруг и "вблизи движущегося электрона есть сопутствующая, "присоединенная" масса полевой материи, в которой создаются эти волновые свойства, описываемые некоторой волновой функцией

? = f(x, y, z, ?, t),

где x, y и z - пространственные координаты;

? - скорость движения электрона;

t - момент времени.

Считается, что движение электрона вдоль круговой орбиты следует уподоблять замкнутому электрическому току J. Получается как бы вращающийся заряженный "обруч" (рис. 11), который обладает механическим моментом L количества движения и направленным в противоположную сторону, магнитным моментом P_m, кратным электромагнитному моменту, называемому "магнетиком Бора". На рис. 11 упрощенно показана планетарная модель атома водорода с одним электроном на орбите [47. Т. III. С. 312]. Другие водородоподобные структуры атомов имеют на орбите определенного пространственно-энергетического уровня несколько электронов, а представление о круговых орбитах вокруг ядра многих электронов остается подобным модели атома водорода.

0x01 graphic

Рис. 11. Упрощенная планетарная модель атома водорода

Из приведенной модели орбиты электрона не видно силовых магнитных линий, хотя указаны механический и магнитный моменты. Если показать магнитные линии и движение электронов, порождающее магнитное поле, то модель атома водорода будет иметь вид, приведенный на рис.12. Здесь спиралеобразной линией показано вращение электрона вокруг своей оси и вдоль движения по орбите. Это собственное вращение электрона, т.е. его спин, создает элементарное орбитальное магнитное поле Н₀.

Известный ученый В. Гейзенберг доказал, что по причине волновых свойств электронов и статистического характера скорости и неустойчивости пространственных координат (отклонений от срединной линии траектории) движущегося электрона его местоположение невозможно точно определить. Можно только указать некоторую область существования (нахождения) движущегося электрона. В этом состоит смысл принципа неопределенности Гейзенберга.

Позднее Э. Шредингер написал неопределенное уравнение квантово-волновой функции электрона

0x01 graphic
,

где ? - некоторая волновая функция; x, y, z - координаты; m - масса электрона; r - расстояние до ядра; h - постоянная Планка; е - заряд электрона; Е - полная энергия электрона.

0x01 graphic

Рис. 12. Уточненное представление орбиты планетарной модели
атома водорода (N и S - магнитные полюса)

Уравнение Шредингера составлено для случая водородоподобных атомов, когда, предположительно, электрон вращается вокруг ядра по круговой орбите и взаимодействует исключительно только с центральным полем ядра. В уравнении Шредингера взаимодействие электронов между собой не учитывается, а волновая функция ? не определена.

Следует отметить и еще одно достижение планетарной модели атома.

Бесспорно, что орбиты движущихся электронов в атоме не произвольны, не хаотичны, а строго определенные. Орбиты электронов группируются по слоям (пространственно-энергетическим уровням). Энергии электронов каждого слоя практически равны друг другу. Энергии электронов, орбиты которых относятся к разным слоям (уровням), существенно разнятся. "На каждой орбите может одновременно находиться не более двух электронов", отличающихся спинами (от англ. слова spin - веретено), т. е. должны отличаться направлениями своих вращательных движений [47. Т. II. С. 127]. С другой стороны, утверждается в [55. С. 316], что "в определенном стационарном состоянии атома никакие его два электрона не могут находиться в одном и том же состоянии". Это утверждение квантовой теории атома получило название принципа Паули. Так как на орбитах электроны в свободных водородоподобных атомах не могут иметь одинаковые состояния то, следовательно, они не могут находиться на одной орбите. Значит, на каждой орбите должно быть по одному электрону. По Паули, в водородоподобном атоме количество электронов в стационарном состоянии равно N=2n², где n - главное квантовое число. При n=1, как у водородоподобного гелия, на стационарных орбитах электронной оболочки находятся два электрона. Но так как на одной орбите может быть только один электрон, то, очевидно, у каждого электрона гелия своя орбита (нет коллективной орбиты для многих электронов определенного пространственно-энергетического уровня).

Если для двухэлектронного атома гелия планетарная модель противоречива, то для многоэлектронных атомов она не подходит вовсе. Если электроны, находясь каждый на своей орбите, отталкиваются друг от друга, то их наиболее устойчивые круговые орбиты должны расходиться и смещаться относительно ядра, т. е. становиться нецентристскими. Однако ученым еще долгое время трудно было отказаться от привычной планетарной модели атома.

Так, например, в обобщенной атомной теории Н. Бора сохранена планетарная модель - электроны в атомах по-прежнему совершают движения вокруг ядра под действием кулоновских сил. Поэтому теория Бора не могла описать все возможные стационарные состояния движущихся электронов. Известно, что кроме круговых орбит, возможны еще и эллиптические, но все они являются централистскими, в которых движениям электронов задаются траектории с центром, где находится ядро атома, но на самом деле электроны вовсе не обязаны двигаться именно так. Вероятно, возможны и другие конфигурации стационарных орбит движения электронов в атомах. В подтверждение этого "выяснилось, что электронам присущи свойства, не согласующиеся с представлением о планетарном их движении" [55. С. 287].

Важнейшим недостатком планетарной модели атомов является то, что в ней не учитываются взаимодействия электронов и влияние на орбиты электронов неоднородностей структуры ядер.

Давно известно, что ядро любого атома вещества состоит из положительно заряженных протонов и не имеющих электрического заряда нейтронов. Заряд протона по абсолютной величине равен отрицательному (противоположному) заряду электрона. Протон и нейтрон являются двумя зарядовыми состояниями примерно равных по массе ядерных частиц, соединение которых называется нуклоном. Ядро водорода состоит из одного нуклона, то есть из протона и нейтрона. Ядро атома гелия - из двух нуклонов и т.д. по порядку таблицы элементов вещества. Симметричная электрическая неоднородность нуклонов и, следовательно, ядер атомов должна приводить к смещению орбит электронов относительно центра ядра. В этом, кроме взаимного отталкивания электронов, ещё одна из причин формирования нецентристской (непланетарной) электронной структуры атомов.

Простейшие непланетарные (нецентристские) модели электронных орбит атомов предложены нашими соотечественниками В. К. Григоровичем [34-37] и М. М. Протодьяконовым [86-88].

4.2. Непланетарные модели атома

С помощью планетарной модели атомов невозможно объяснить их взаимосвязи в молекулах, в кристаллических решетках, в разнообразно структурированных и аморфных твердых телах. Поэтому начиная, по-видимому, с В. Гейтнера и Ф. Лондона (1927 г.) вплоть до наших дней предпринимались многочисленные попытки преодоления вышеназванной трудности на пути отказа от планетарной модели атома.

Если исходить из широко распространенного представления о металлах, то, естественно, необходимо признать, что взаимодействие коллективизированных электронов с ионами в металлических решетках является ненаправленным и, при сферической симметрии внешних электронных оболочек ионов, должно приводить к плотным кристаллическим упаковкам. Однако большинство металлов имеют неплотные структуры, и расстояния между соседними ионами не всегда одни и те же. По утверждению В. К. Григоровича, это "свидетельствует о наличии направленных связей и требует введения представлений о несферической симметрии ионов" [34. С. 204].

Попытки связать только внешние электроны попарно в валентные связи предпринимались Л. Полингом, В. Юм-Розери и др. Однако эти попытки не дали достаточно убедительного объяснения связи кристаллической структуры металлов с их электронным строением. Кроме того, это в корне подрывало представление о "свободных электронах" - электронах проводимости и поэтому всерьез не принималось.

В последние годы В. К. Григорович предложил теорию, в значительной степени устраняющую многие противоречия и недостатки укоренившихся представлений об электронной структуре металлов.

Так, например, В. К. Григорович, исследовав микроструктуры металлов и сплавов и их свойства, предложил принципиально новый подход "построения квантово-механической теории, объясняющей структуру металлов, основанную на объединении модели коллективизированных валентных электронов, взаимодействующих с решеткой, с представлениями об образовании валентных ?-связей между подвалентными электронами внешних оболочек ионов". Сущность "такого подхода заключается в сохранении за валентными электронами в металле функции осуществления металлического взаимодействия с решеткой и электронных свойств металла и в привлечении к образованию направленных связей, определяющих структуру металла, ранее не учитывающихся подвалентных электронов внешней оболочки металлических ионов. Такая модель позволяет дополнить электронную теорию металлов представлениями квантовой химии о валентных связях" [35].

Исходя из анализа уравнения Шредингера В. К. Григорович пришел к выводу, что "для всех ?-состояний электронов ...независимо от главного (квантового. - В. Ф.) числа n, волновые функции представляют гантели, вытянутые вдоль осей прямоугольных координат... Гантелеобразную форму имеют и d-орбитали... Главными типами валентных связей в молекулах и ковалентных кристаллах являются двухэлектронная двухцентровая обменная ?-связь и двухэлектронная ?-связь" [36. С. 44-45].

Устойчивая связь между атомами, по представлению В. К. Григоровича, обеспечивается частичным перекрытием крайней части гантелеобразных орбит валентных электронов взаимосвязанных атомов. На рис. 13 приведены электронные структуры отдельных молекул водорода, фтора, кислорода и азота [36. С. 46].

0x01 graphic

Рис. 13. Образование ?- и ?-связей в молекулах водорода, фтора,

кислорода и азота

Приведем структуры некоторых типов кристаллов. На рис. 14 показана кубическая (а) и объемно-центрическая кубическая структура (б) кристаллической решетки [36. С. 94].

а б

Рис. 14. Металлические связи в кристаллических структурах:

а - кубическая и б - объемно-центрическая кубическая (ОЦК) решетки

Представление об электронной структуре атомов, развиваемое В. К. Григоровичем и другими учеными, в значительной степени оправданно и во многих случаях хорошо согласуется с экспериментальными данными. Однако и такое представление не решает полностью проблему межатомной связи, ибо остается невыясненным сам механизм этой связи - механизм взаимодействия электронов, орбиты которых пересекаются. Пересечение траекторий частиц (электронов) не требует однозначно их взаимодействия, обеспечивающего устойчивую, постоянную связь между ними, стабильность межатомной связи, устойчивость кристаллической решетки. Все это привносится, постулируется и считается само собой разумеющимся.

Радикальным в гипотезе В. К. Григоровича является то, что межатомное, структурообразующее взаимодействие металлов переносится на второй электронный уровень, оставляя внешний электронный уровень свободным от участия в кристаллообразовании межатомных связей, "при этом полностью сохраняется теория свободных электронов... поскольку внешние валентные электроны не привлекаются к объяснению направленных связей" [34. С. 213]. Но остаются ли эти внешние, свободные от установления направленных связей, электроны при своих атомах или обобществляются? Вопрос можно сформулировать несколько иначе. Возникает ли электронный газ в момент начала передачи электрической энергии через металл или свободные электроны присутствуют в металле и в то время, когда в нем нет электрического тока?

Из модели Григоровича и зонной теории действительно следует вывод, что внешние электроны атомов металлов должны быть "почти свободными", т. е. с относительно малой энергией взаимосвязи с ядром. При воздействии на эти электроны разности потенциалов электрического поля происходит:

-- отрыв электронов (внешних, "почти свободных");

-- их движение в направление действия силы.

Так появляется ток проводимости. В этом случае внешние электроны действительно коллективизируются, но при возникновении электрического тока, а не до этого.

Для решения проблемы "сверхпроводимости" в ее прежнем названии, т. е. для объяснения сверхнамагничиваемости, модель электронного строения атомов и тел, по В. К. Григоровичу, не подходит, так как в ней нет места пространственным диполям (атомным микромагнитикам) и поэтому нет наглядного (модельного) представления о природе магнетизма: ферромагнетизма, парамагнетизма, диамагнетизма и сверхмагнетизма.

В модели В. К. Григоровича электроны в атоме двигаются независимо друг от друга, т. е. электроны будто бы не взаимодействуют между собой, а должны отталкиваться как одноименные (отрицательные) электрические заряды.

Кроме оригинального представления В. К. Григоровича о внутреннем строении атомов и металлов, есть и другая непланетарная модель атомов и твердых тел М. М. Протодьяконова. В своих работах [86, 87, 88] М. М. Протодьяконов в корне порывает с идеей свободных, обобществленных электронов в металлах, находящихся в непроводящем (нормальном) состоянии. Кроме того, он показал, что волновое уравнение Э. Шредингера написано для одного электрона в атоме, т. е. только для водорода, в котором электрон по теории должен вращаться вокруг ядра. Но и в этом случае планетарная модель не вполне годится. Спутники планет вращаются по одной фиксированной для них орбите, а не самопроизвольно, тогда как считается, что электрон в атоме водорода и электроны в водородоподобных атомах вращаются по самопроизвольно меняющимся в пространстве положениям круговых орбит. Однако М. М. Протодьяконов показал, что в одноэлектронном решении уравнения Э. Шредингера волновая функция симметрична и наибольшие вероятности прохождения круговой орбиты электрона вытянуты вдоль трех произвольных осей прямоугольных координат x, y и z. Уравнение Шредингера составлено для случая таких водородоподобных ядер, в которых электроны взаимодействуют только с центральным полем ядра. В уравнении Шредингера взаимодействие электронов между собой не учитывается. Однако ясно, что даже в случае двух электронов в атоме каждый электрон движется в нецентральном поле и поэтому его орбита не обязательно является сферической и центральной - сказывается поле электронов и пространственная неравномерность поля ядра.

В уравнение Шредингера, вообще говоря, необходимо ввести дополнительные члены, учитывающие нецентральность поля, в котором вынуждены двигаться электроны всех атомов. Но даже само "...уравнение Шредингера для системы трех тел не может быть точно проинтегрировано. Тем более это относится к последующим атомам, содержащим 4, 5, 6 и т. д. частиц" (М. В. Волькенштейн). Учет нецентральности поля, в котором движутся электроны, делает решение уравнения Шредингера невозможным. В теперешнем его виде найти решение для атома с Z=100 невозможно, "даже если покрыть всю поверхность Земли электронными вычислительными машинами и заставить их непрерывно работать столько времени, сколько существует наша галактика" [50. С. 7].

Но, оказывается, существует другой метод, позволяющий построить электронную модель атомов, не противоречащую квантово-волновой механике. Собственно именно такой метод разработан профессором М. М. Протодьяконовым.

В основание электронной модели атомов М. М. Протодъяконова положено представление о том, что, отталкиваясь друг от друга, электроны стремятся к такому динамическому взаимному расположению, при котором каждый из них был бы в наименьшей степени экранирован от ядра зарядами прочих электронов. Это возможно только при некотором симметричном расположении электронов [87].

При моделировании структур атомов и их соединений М. М. Протодьяконов рассматривал структуры только внешних (валентных) орбит электронов в виде тороидов, аналогичных показанным на рис. 11 и 12. Изображения атомов с двумя и тремя тороидовидными орбитами валентных электронов показаны на рис. 15 [51].

0x01 graphic

а б

Рис. 15. Схемы электронных оболочек атомов с двумя (а - гелий)

и тремя (б - литий) электронами

Схема строения графита по М. М. Протодьяконову приведена на рис. 16.

0x01 graphic

Рис. 16. Схемы электронных оболочек графита:

а - шестиугольное углеродное кольцо; б - решетка в плане

Приведем для большей убедительности и наглядности еще две структуры кристаллов. На рис. 17 показана структура граней кубической решетки [87] и структура кристалла льда [88].

0x01 graphic

а б

Рис. 17. Схемы электронных оболочек:

а - на гранях куба; б - структура кристалла льда (в плане)

Принципиально важным в протодьяконовских моделях является то, что, во-первых, тороидовидные орбиты имеют все электроны сложного атома и их расположение не центрировано относительно ядра атома, как это у единственного электрона водорода; во-вторых, при наличии четного количества валентных электронов в атоме два электрона образуют связанные пары (магнитные диполи), при этом электроны находятся на противоположных сторонах от центра атома (ядра); в-третьих, соединение атомов обеспечивают (осуществляют) взаимодействующие электроны посредством своих электромагнитных полей.

Однако модели атомов, их электронные структуры не рассмотрены М. М. Протодьяконовым в целом, т. е. во всем объеме атомов, а только с позиций учета внешних валентных электронов атомов породообразующих минералов и сходных с ними веществ.

В порядке уточнения и развития моделей М. М. Протодьяконова попытаемся построить более подробные электронные модели атомов, основываясь на некоторых фактах и соответствующих им предположениях.

4.3. Уточненная модель структур атомов и их связей

В порядке развития теории и атомных моделей М.М. Протодьяконова была предложена автором в соавторстве с профессором Т.А. Лебедевым еще в 1968-1971 годах уточненная модель строения атомов, молекул и кристаллов [63-65].

Признается, что на установление одной устойчивой связи атомов в твердом теле каждый атом "отдает" ("задействует") один электрон из своего пространственно-энергетического уровня электронной структуры, формирующего межатомную структуру. Поэтому максимальное число электронов структурообразующего уровня не может быть больше числа возможных непосредственных связей данного атома с другими атомами. Если мы обратимся к кристаллическим структурам, и в частности к кристаллическим структурам металлов, то увидим, что отдельные атомы в элементарных (простейших) ячейках имеют следующее количество связей: в кубической решетке - 6, а в октаэдрической - 8. Все другие, т. е. сложные кристаллические структуры, состоят из соединения элементарных ячеек. Так, например, объемно-центрированная кубическая (ОЦК) решетка состоит из двух простых кубических решеток, "вставленных" одна в другую. Гранецентрированная кубическая (ГЦК) решетка есть комбинация четырех простых кубических решеток.

В вышеназванных элементарных, или простых, ячейках число связей единичного атома равно координационному числу. Координационное число К - это количество соседних атомов, непосредственно окружающих каждый атом в кристаллической решетке. Но это не значит, что со всеми соседними атомами находится во взаимодействии любой конкретно рассматриваемый атом решетки. В ячейке объемно-центрированной кубической решетки близлежащих к данному атому находятся 8 соседних атомов и К=8. Но так как в ОЦК-решетке две сочлененных кубических решетки, то каждый атом в ней имеет 6 связей, К=6. В гранецентрированной кубической решетке координационное число К=12, но так как в ГЦК-решетке соединены четыре кубических решетки, то и в ГЦК-решетке К=6. Кроме того, в ГЦК-решетке, если соединить атомы, находящиеся в центрах плоскостей (граней) куба, то получается фигура октаэдр с K=8. Такой же октаэдр можно усмотреть внутри двух соседних объемно-центрированных ячейках кристаллической ОЦК-решетки. У гексагональной плотноупакованной решетки, при отношении с/а = = 1,633, где с - наибольшее расстояние между центрами ближайших атомов в ячейке; а - наименьшее расстояние между соседними атомами ячейки, получается при подсчетах, что координационное число равно 12. Но у многих атомов, имеющих гексагональную кристаллическую решетку, отношение с/а находится в пределах 1,57-1,64. Считается, что если с/а отличается от 1,633 (как, например, у цинка и кадмия), то координационное число и гексагональной решетки равно 6. Есть сведения, что у цинка и ртути координационное число К=16, а если они в плотноупакованной гексагональной решетке, то К=12 [47, рис. 16]. Но цинк и ртуть, а также многие другие атомы металлов, имея, как считается, по два валентных (внешних) электрона, не могут с их помощью создать сложную кристаллическую решетку. Из этого следует, что "ответственными" за кристаллизацию являются, по существу, электроны полностью (или почти полностью) заполненных уровней электронной структуры атомов. Координационное число К=16, вероятно, свидетельствует о том, что в условиях плотноупакованной гексагональной решетки эти атомы имеют в структурообразующем уровне K=16:2=8 электронов.

На основании вышеизложенного можно утверждать, что электронное строение атомов подчиняется периодической закономерности заполнения электронных оболочек соответствующего уровня, которая представлена в табл. 2.

Числа 6 и 8 в подлинной таблице Д. И. Менделеева (см. табл. 3) являются определяющими свойства и структуру периодической системы элементов вещества. В его таблице 8 групп и 6в2=12 рядов. Но если считать, что в одном периоде по два полных ряда элементов, как это принято для средней части современной "Таблицы Менделеева", то получается 8 периодов.

Таблица 2

Распределение электронов по периодам

Номера периодов	1	2	3	...	8
Номера электронных уровней (слоев)	1	2	3	4	5	6	...	15	16
Обозначение электронных уровней	S₁	P₁	S₂	P₂	S₃			P₃		...	S₈	P₈
Максимальное количество электронов	6	8	6	8	6			8		...	6	8

Принимая основные предпосылки построения протодьяконовских моделей атомов, в частности учитывая отталкивание электронов друг от друга и взаимопритяжение электронов и протонов в атоме, а также несимметричность электрического поля нуклона (нейтрона и протона) из-за экранирующего действия более крупного нейтрона, чем протон (антиэлектрон), получаем следующие модели структур атомов. Так, например, электрон в атоме водорода вращается по круговой орбите, но не вокруг ядра, а с большим смещением от ядра. Структура атома водорода приведена на рис. 17. В свободном атоме гелия (Не) электроны создают электронный магнитный диполь (магнитон) как это показано на рис. 18. Двухатомная молекула водорода Н₂ имеет вид схематически показанный на рис. 19. Модели атомов лития и бериллия изображены на рис. 20 и 21. Очевидно, что электронная структура атомов зависит от структур их ядер. Аналогичное представление о структуре атомов развивает Ф.М. Канарёв [53 и др.].

0x01 graphic

Рис. 18. Модель атома водорода: е - электрон, r - радиус орбиты электрона

0x01 graphic

Рис. 19. Модель атома гелия

Таблица 3

Перiодическая система элементовъ по группамъ и рядамъ [36]

Ряды.

Г Р У П П Ы Э Л Е М Е Н Т О В Ъ:

III

VII

VIII

Водо-

родъ.

1,008

Гелiй.

Не

4,0

Ли-

тiй.

7,03

Берил-

лiй.

Ве

9,1

Боръ.

11,0

Угле-

родъ.

12,0

Азотъ.

14,01

Кисло-

родъ.

16,0

Фторъ.

19,0

Неонъ.

19,9

На-

трiй.

23,05

Маг-

нiй.

24,36

Алю-

минiй.

27,1

Крем!

нiй.

28,2

Фос-

форъ.

31,0

Сера.

32,06

Хлоръ.

35,45

Ар-

гонъ.

Ка-

лий.

39,15

Каль-

цiй.

Са

40,1

Скан-

дiй.

44,1

Ти-

танъ.

48,1

Вана-

дiй.

51,2

Хромъ.

52,1

Мар- ганецъ.

55,0

Же- Ко- Ник-

лезо, бальтъ. хель

Fe Co Ni (Cu)

55,9 59 59

Медъ.

63,6

Цинкъ.

65,4

Гал-

лiй.

70,0

Гер-

манiй.

72,5

Мышь-

якъ.

Се-

ленъ.

79,2

Бромъ.

79,95

Крип-

тонъ.

81,8

Ру-

бидiй.

85,5

Стро-

цiй.

87,6

Ит-

трiй.

89,0

Цир-

конiй.

90,6

Нiо-

бiй.

94,0

Молиб-

денъ.

96,0

Ру- Ро- Пал-

тенiй. дiй. ладiй.

Ru Rh Pd (Ag)

101.7 103.0 105.5

Сере-

бро.

107,93

Кад-

мiй.

112,4

Ин-

дiй.

115,0

Оло-

во.

119,0

Сурь-

ма.

120,2

Тел-

луръ.

127

Iодъ.

127

Ксе-

нонъ.

128

Це-

зiй

182,9

Ба-

рiй.

187,4

Лан-

танъ.

138,9

Це-

рiй.

140,2

Иттер-

Бiй.

173

Тан-

талъ.

183

Вольф-

рамъ.

184

Ос- Ири- Пла-

мiй. дiй. тина.

Os Jr Pt (Au)

191 193 194,8

Зо-

лото.

197,2

Ртуть.

200,0

Талiй.

204,1

206,9

Вис-

мутъ.

208,5

Радiй.

225

Торiй.

232,5

Уранъ.

238,5

Комментарии: 5, последний от 24/01/2022.

Обновлено: 12/04/2019. 450k. Статистика.

Монография: Естеств.науки

Связаться с программистом сайта.

Федюкин Вениамин Константинович Теория сверхдианамагничиваемости взамен ошибочной теории сверхэлектропроводимости тел

Федюкин Вениамин Константинович
Теория сверхдианамагничиваемости взамен ошибочной теории сверхэлектропроводимости тел