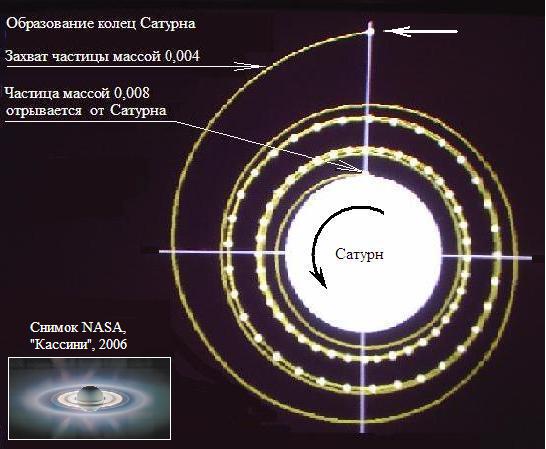
Программа, показывающая образование колец
Сатурна.
Среда программирования ТУРБО
ПАСКАЛЬ 5.5.
uses Crt, Graph; label M1,M2; var Gd,Gm,Xo,Yo,Rn,Dx,Dy,Rs,J,F,N,N1:Integer; Ar,At,Z,S,R,Ct,Cr,B,A,T :Real; Massa,Alfa,Betta,Gamma,U,Ux,Uy :Real; I :LongInt; begin {Включение графического режима} Gd := Detect; InitGraph(Gd,Gm,'B:\Tp55\BGI'); if GraphResult <> grOk then Halt(1); {----------------------------------------------------------------} SetColor(15); SetTextStyle(TriplexFont,HorizDir,1); {Заголовок} MoveTo(0,0); OutText('Образование колец Сатурна'); Xo:=Round(GetMaxX*2/3-50); Yo:=Round(GetMaxY/2); {Начало осей} Line(150,Yo,GetMaxX-50,Yo); Line(Xo,0,Xo,GetmaxY-30); {Оси X и Y} Rs:=80; Pieslice(Xo,Yo,0,360,Rs); {Рисование Сатурна} T:=0.005; {Шаг отсчёта времени} A:=2; B:=250; Ct:=3000; Cr:=10; {Эмпирические константы} {A-отражает воздействие силы тяготения, не зависящей от расстояния} {B-отражает воздействие силы тяготения Ньютона,создаваемой Сатурном} {Ct-отражает воздействие тангенциальной составляющей вихревых сил} {Cr - отражает радиальное воздействие вихревых и центробежных сил} {----------------------------------------------------------------} { Образование первого кольца } {Оси координат и частицы вращаются синхронно с Сатурном, поэтому начальные скорости частиц в программе не отражены} OutTextXY(0,GetMaxY-50,'Захват частицы массой 0,004'); Massa:=0.004; N:=142; N1:=109; {Масса частицы и количество шагов} Rn:=150;R:=Rs+Rn; {Расстояние от частицы до Сатурна и его центра} F:=1; {Установка флага} M1: Dx:=Xo; Dy:=Yo-Round(R); {Начальные координаты частицы} MoveTo(Dx,Dy); Pieslice(Dx,Dy,0,360,3); {Начало траектории} SetColor(14); {Цвет траектории} J:=1; repeat Z:=Yo-Dy; S:=Xo-Dx; {Расстояния от частицы до осей X и Y} R:=Sqrt(Z*Z+S*S); {Расстояние от частицы до центра Сатурна} if S=0 then S:=0.00001; {Защита от деления на ноль} Alfa:=ArcTan(Z/S); {Угол наклона радиуса-вектора} At:=Ct/R/Massa; {Тангенциальное ускорение} Ar:=(A+B/R/R+Cr/R)/Massa; {Сумма радиальных ускорений} U:=Sqrt(At*At+Ar*Ar); {Амплитуда вектора полного ускорения} {Вычисление проекций полного ускорения на оси координат} Betta:=ArcTan(Ar/At); Gamma:=Alfa-Betta; Ux:=U*Sin(Gamma); Uy:=U*Cos(Gamma); {Вычисление текущих координат} if Dx>Xo then begin Dx:=Dx+Round(Ux*T); Dy:=Dy-Round(Uy*T) end else begin Dx:=Dx-Round(Ux*T); Dy:=Dy+Round(Uy*T) end; LineTo(Dx,Dy); {Рисование траектории} if J>N1 then Pieslice(Dx,Dy,0,360,3);{Рисование позиций частицы} for I:=1 to 10000000 do; {Пустой цикл для замедления процесса} J:=J+1; until J>N; SetColor(15); if F=2 then Goto M2; {Проверка флага} {----------------------------------------------------------------} { Образование второго кольца } OutTextXY(0,GetMaxY-25,'Частица массой 0,008 отрывается от Сатурна'); Massa:=0.008; N:=130; N1:=90; {Масса частицы и количество шагов} Rn:=2; R:=Rs+Rn; {Расстояние от частицы до Сатурна и его центра} F:=2; { Установка флага } Goto M1; M2: OutTextXY(GetMaxX-100,GetMaxY-25,'Готово'); Readln; CloseGraph; End.
|
|
Связаться с программистом сайта.