Lib.ru : Путенихин Петр Васильевич. Правила счета элементов бесконечного множества

Rules for counting elements of an infinite set

Вложение: http://lit.lib.ru/img/p/putenihin_p_w/kantor110/kantor102d.pdf

Оглавление

Связь математики и физики

Равномощные множества чисел

Количества натуральных чисел в группах

О счетности континуума - точек на отрезке

Задача об "Отеле Гильберта"

Несостоявшаяся перепись

Разрядность и количество чисел в массиве

Счетность всех мыслимых видов чисел

О равномощности отрезка и квадрата

Стереографическая проекция

Литература

Аннотация

Вскрыты ошибки Кантора и его последователей в логических рассуждениях о бесконечных множествах. Приведено доказательство счетности континуума, счетности всех действительных чисел. Показана ошибочность рассуждений в задаче об "Отеле Гильберта".

The mistakes of Cantor and his followers in logical reasoning about infinite sets are revealed. The proof of the countability of the continuum, the countability of all real numbers is given. The erroneousness of reasoning in the problem of "Hilbert's Hotel" is shown.

Ключевые слова: множество, бесконечность, равномощность, число, биективное соответствие, противоречие, многомерное пространство, расширение Вселенной, Кантор

Связь математики и физики

Давно замечено интересное и важное свойство математики, которая позволяет делать верные, но изначально просто как бы выдуманные описания нашего мира, предсказания:

"Существует вопрос, давно волнующий людей, задумывающихся об основаниях математики: почему математика столь эффективна при описании нашего мира и столь хорошо описывает его эволюцию? ... Почему эти правила так хорошо работают?" [6]

Однако вряд ли следует слишком уж сильно этому удивляться и вспоминать еще одно её такое же удивительное свойство: способность дать любой желаемый результат. Эта математика так хорошо работает просто потому, что мы и вывели её из прямых наблюдений за окружающей действительностью. Эффективно работает, значит, верно подсмотрели. Более того, в науке и, в частности, в физике уже давно замечена еще одна интересная закономерность: кажущиеся поначалу абстрактными математические выражения, уравнения вдруг оказываются описанием какого-нибудь вполне реального явления:

"... физики обнаруживают, что математические построения, необходимые им для описания нового класса явления, уже исследованы математиками по причинам, не имеющим ничего общего с обсуждаемыми явлениями" [2, с.264].

Однако даже при таком явно полезном подходе следует все-таки быть предельно осторожным при формулировке выводов и следствий из этих математических построений. Можно привести ряд примеров, когда такие выкладки приводят не просто к противоречиям со здравым смыслом, но к довольно заметным противоречиям с логикой, содержат логические ошибки. Например, одним из наиболее известных таких странных выводов при исследовании бесконечных множеств элементов являются доказательства Кантора о равенстве числа точек на квадрате и линии, равной длине его ребра.

Приведённые в статье выкладки опубликованы в авторской книге [11].

Равномощные множества чисел

В литературе по космологии встречаются весьма любопытные рассуждения о тождественных бесконечностях. В частности делается очевидный ошибочный вывод о том, что в бесконечности часть может быть равна целому:

"множество натуральных чисел (ℕ) равномощно множествам целых чисел (ℤ), чётных натуральных чисел, всех рациональных чисел (ℚ), а отрезок числовой прямой (𝕀 = [0,1], континуум) оказывается в биективном соответствии со всей числовой прямой (ℝ), а также с n-мерным евклидовым пространством (ℝⁿ)" [1].

Несомненно, это противоречит нашей интуиции. Ведь четные числа явно составляют лишь половину всех целых чисел. Это справедливо для любой конечной совокупности чисел, но, как утверждается в цитате, не соответствует бесконечным рядам, для которых получается, что их количества равны. А утверждение в отношении отрезка буквально означает, что всем точкам отрезка соответствуют все точки всей евклидовой бесконечной плоскости. Такие же странные выводы о соотношении целого и части делаются и в космологии [7, с.77; 2, с.282].

И эти противоречащие здравому смыслу и логике выводы преподносятся в научно-популярной литературе, в книгах, в документальных фильмах (BBC) как строго доказанные факты. Ошибочность подобных методов можно показать, если произвести подсчет количеств натуральных чисел при различных способах их группирования, приводящие к любому произвольному результату.

Для доказательства указанной равномощности точек отрезка и квадрата Кантор использует противоречивый, нелогичный метод. Конечно, можно предположить, что методология и доказательства Кантора и приведенные в цитате утверждения являются узкими теоретическими, частными проблемами. Однако они в явном виде использованы для того чтобы поставить под сомнение, например, одно из основных положений понятия многомерности:

"... параметрическое определение размерности (по крайней мере в форме: "Размерность пространства -- это минимальное число параметров, которые необходимы, чтобы отличать точки пространства друг от друга") математически некорректно. Это стало ясно после построенного Георгом Кантором (1845--1918) знаменитого примера взаимно-однозначного соответствия между множествами точек квадрата и отрезка" [4, с.32].

Рассмотрим некоторые доказательства, которые позволят решительно отвергнуть аргументы Кантора.

Количества натуральных чисел в группах

Нумерация четных чисел. Например, в одном из вариантов для доказательства равномощности предлагается записать четные числа в виде бесконечного ряда, а под этим рядом написать их порядковые номера из натурального ряда чисел [7, с.78]:

kantor (1)

Здесь каждому четному числу соответствует один порядковый номер из натурального ряда чисел и наоборот. Значит, утверждается, число четных чисел равно числу всех чисел натурального ряда.

Но это неверно. В частности, в данном примере четные числа не являются частью ряда натуральных чисел, это совершенно самостоятельный ряд, в котором вместо четных чисел могли быть любые символы.

Ошибка состоит в некорректном способе подсчета, в котором часть элементов исходного ряда просто игнорируется, исключается из процедуры подсчета. Произведём подсчет другим, правильным способом. Возьмем ряд всех натуральных чисел и будем их считать самым обычным, привычным способом. Для этого каждое натуральное число будем класть в соответствующий ящик, и при этом называть его значение: один, два, три и так далее. Одновременно, по мере того, как нам будут встречаться эти числа, мы будем с каждым четным числом класть такую же цифру во второй ящик. И, для наглядности, с каждым нечётным - в третий ящик. Ну, и для ещё большей наглядности - для каждого пятого числа - в четвертый ящик.

Через некоторое время посмотрим, что у нас в ящиках? Через тысячу шагов, очевидно, в первом ящике будет 1 000 чисел. Во втором и третьем - по 500, а в четвертом - только 200. Ну, или в виде соотношения 10:5:5:2.

Продолжим раскладывать числа и вновь проверим содержимое ящиков теперь уже через 10 000 шагов. И в этот раз мы обнаружим, что количества чисел в ящиках соотносятся как 10:5:5:2. Нужно ли доказывать, что и через миллион, и через миллиард, и через гугл шагов количества чисел в ящиках будут соотноситься как 10:5:5:2?

Если мы последовательно синхронно считаем количества чисел в натуральном ряду, то мы найдём истинное соотношение их количеств. Однако говорить, что бесконечное число всех натуральных чисел больше, чем число всех четных или нечетных чисел не совсем правильно. Эти числа образуют бесконечности, и следует говорить только об их мощности:

бесконечность всех натуральных чисел в два раза мощнее, чем бесконечности всех четных или нечетных чисел и в пять раз мощнее, чем бесконечность всех чисел, кратных пяти.

Утверждение, что часть может равняться целому ошибочно в самой формулировке. Мощность части бесконечности всегда меньше мощности всей бесконечности.

Рассмотрим приведённый выше пример в терминах мощностей. Примем без доказательства, что количество членов множества и его мощность - это разные, но схожие по смыслу понятия. Мы не можем сравнивать число членов множеств, по определению равных бесконечности, но мы можем сравнивать их мощности. Отношение мощностей М₁ и М₂ равномощных множеств всегда равно конечному числу:

kantor

В этом случае отношение множеств (1) для четных чисел запишется в виде:

kantor

Запишем также и отношение множеств для нечетных чисел:

kantor

Далее нам понадобится и такое тождественное отношение:

kantor

Это равенство очевидно, поскольку числитель равен знаменателю. Теперь просуммируем эти приведенные два отношения мощностей:

kantor

Очевидно, что последняя дробь содержит в числителе все целые натуральные числа:

kantor

поэтому они и равны тождественно единице.

Это определённо означает, что мощности множеств всех натуральных чисел и суммы множеств всех четных и нечетных чисел равны. Но это также означает и тождественное равенство их бесконечного количества членов. Очевидно, что множества четных и нечетных чисел равномощны, поэтому, разделив полученное равенство на c_n, получим:

kantor

Поэтому из равенства также следует, что каждая из мощностей четных и нечётных чисел в два раза "слабее" мощности всех натуральных чисел:

kantor

Отметим также без доказательств, что любые действия над каждым членом множества не изменяют мощности множества:

Из этого непосредственно следует, что решающее значение имеет способ, каким получено множество. Например, множество всех четных чисел может быть получено удалением из множества всех натуральных чисел нечётных или умножением на 2 каждого члена множества всех натуральных чисел:

Казалось бы, последнее выражение является точной копией множества всех четных чисел М(2, 4, 6, 8...). Но это ошибочно, поскольку любые действия над всеми (или отдельными) членами множества не изменяют их полного количества и, соответственно, мощности. Поэтому справедливо (знак множества M опускаем):

kantor

Хотя оба множества в числителях в обеих строках выглядят тождественно, на самом деле это разные множества, имеющие разную мощность.

Перестановки в рядах. Еще один вариант доказательства равномощности части и целого приведен в книге [2, с.282], где предлагается вести подсчет нечетных чисел, предварительно переставив их в ряду:

"В бесконечной вселенной коэффициент объема можно определить как долю, занятую областями данного типа. Но это определение приводит к неоднозначности. Чтобы проиллюстрировать природу проблемы, зададимся вопросом: какова доля нечетных чисел среди целых? Четные и нечетные числа чередуются в последовательности 1, 2, 3, 4, 5, и можно подумать, что ответом, очевидно, будет половина. Однако целые числа можно упорядочить другим способом. Например, так: 1, 2, 4, 3, 6, 8 ... Эта последовательность по-прежнему включает все целые числа, но теперь за каждым нечетным числом следует два четных, и кажется, что только треть целых чисел являются нечетными"

Здесь нам отчетливо видна некорректность и противоречивость такой модификации числового ряда, которая строго последовательно и логично легко доводится до абсурда. Для этого все нечетные числа поместим в самый конец бесконечной последовательности. Теперь при поверхностном анализе последовательности мы обнаружим, что в ней нечетных чисел нет вообще. Конечно, мы догадываемся, что все они где-то дальше, но, как бы долго мы ни просматривали последовательность, мы никогда не встретим в ней ни одного нечетного числа. Однако итог явно абсурден: нечетные числа точно есть, но мы их почему-то не пересчитываем. Причина заключается просто в выборе метода подсчета: игнорирование длины ряда. Мы же сами каким-то образом перенесли нечетные числа в конец ряда? Ну, так и нумеровать тогда следует весь ряд. Это же относится и к предложенному выше методу упорядочивания. Каким-то образом эти числа перетасованы? Вплоть до последнего. Ну, так и считать следует соответственно - до последнего числа. Если же числа перетасовываются в процессе счета, тогда "временно вынутые из ряда нечетные числа" все время будут где-то скапливаться. Трудно будет не заметить это бесконечно большое хранилище нечетных чисел.

С другой стороны, мы можем проделать то же самое и с четными числами, например, получив в результате, что их в общем ряду только треть. Иначе говоря, один и тот же метод показывает, что среди целых чисел нечетных одновременно только половина и только две трети. Понятно, что методика, дающая два взаимоисключающих результата не вызывает доверия.

Группировка степеней. Такие методики пересчета, отождествления всегда содержат плохо скрытую подмену понятий. Например, с рядом натуральных чисел отождествляется ряд степеней 10¹, 10², 10³ ... 10ⁿ... и так далее. Таким же образом устанавливается взаимно однозначное соответствие и между множеством натуральных чисел и множеством всех квадратов натуральных чисел 1², 2², 3², ... n²... и так далее. Но принять такое отождествление нет никаких оснований.

Нужно просто обратить внимание на то, что же именно отождествляется. В обоих приведенных примера сразу же можно заметить присутствие члена натурального ряда. Понятно, что отождествляются не значения членов ряда, а их порядковые номера, которые самым наглядным образом обозначены в каждом из членов рядов. До начала отождествления каждый член ряда уже имеет свой натуральный порядковый номер, а значение самого члена ряда не имеет никакого смысла. Это могут быть и летучие обезьяны с соответствующей биркой на шее, и протоны в бесконечной Вселенной, которые ещё только предстоит пометить соответствующим номером, и даже множество миров Эверетта.

Группировка в пары. Попробуем теперь просто пересчитать, перенумеровать все натуральные числа, предварительно соединив их в пары четное-нечетное число: (1,2), (3,4), (5,6), то есть, присваивая каждой паре последовательно номера 1, 2, 3, 4 и так далее. Очевидно, что каждой паре будет присвоен один номер, натуральное число. И мы получаем явное противоречие, поскольку это означает, что количество всех натуральных чисел, собранных в пары, в два раза больше количества всех натуральных чисел. Буквально, количество всех натуральных чисел в два раза больше количества всех натуральных чисел. Но натуральные числа можно группировать и тройками, пятерками, десятками и так далее.

Десять рядов. Еще более наглядно подмена понятий будет видна, если составить из натурального ряда десять новых рядов, каждый из которых содержит натуральные числа, оканчивающиеся на 0, 1, 2 и так далее до 9. Если теперь пересчитать их количества, то для каждого ряда, как и в случае (1) мы получим количество, совпадающее с количеством натуральных чисел. Теперь вновь соединим все эти ряды в единый. Очевидно, что в результате мы получим исходный ряд - натуральные числа. Получается, что количество членов просуммированного ряда в десять раз больше, чем в ряду натуральных чисел. Но ведь просуммированный ряд - это тот же самый натуральный ряд. Здесь совершается та же ошибка: подсчет без учета принадлежности чисел выделенных рядов исходному, натуральному ряду.

Квадратная таблица. Однако и это не предел. Можно, например, составить таблицу из n строк натуральных чисел, поэтому, соответственно, столбцов будет тоже n, где n - натуральное число. Теперь подсчитаем, перенумеруем диагональным процессом Кантора все числа этой таблицы. Очевидно, что каждое из чисел получит свой порядковый номер, которых, понятно, будет ровно n, стремящееся к бесконечности. Но таблица определенно содержит n² элементов. Получается, что количество n² элементов равно n, или, другими словами, количество всех натуральных чисел равно квадрату количества всех натуральных чисел. Конечно, сами натуральные числа к этому непричастны. Проблему создаёт выбор специфических способов подсчета, в основе которых явно лежат методы Кантора, позволяющие получить любой, произвольный результат. Поскольку один и тот же метод при корректном применении даёт разные результаты, такой метод не может быть верным.

О счетности континуума - точек на отрезке

Как утверждается со ссылкой на методологию счета Кантора, множество всех действительных чисел несчетно, то есть, невозможно их пересчитать, присвоив каждому из них некоторое натуральное число - номер, поскольку всегда останутся непронумерованные числа [3, с.73-74]. Вообще-то, на первый взгляд, интуитивно это выглядит вполне очевидно. Рассмотрим, например, следующую явно бесконечную последовательность действительных чисел:

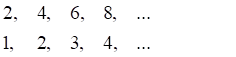kantor (2)

В этих числах запятая просто занимает позицию n, представляющую натуральное число, поэтому чисел в указанной последовательности в точности равно числу строк, n, где n равно бесконечности. Поскольку все номера натуральных чисел использованы для нумерации этих действительных чисел, то очевидно, что остальное множество действительных чисел осталось без номеров, то есть их множество - несчетно. В связи с хитростями нумерации, как правило, вспоминают математика Кантора, который, как считается, доказал, что число точек на отрезке прямой сосчитать никаким способом нельзя. Утверждается, что их нельзя перенумеровать с помощью бесконечного ряда натуральных чисел, приписывая каждой точке свой номер, в каком бы порядке мы ни выбирали эти точки. Всегда останется хотя бы одна точка, на которую не хватит номера!

Перенумеровать или, тождественно, пересчитать бесконечное количество чего-либо, в том числе, сосчитать точки отрезка, действительно, невозможно физически. Однако приводимое затем доказательство, как правило, начинается со слов: "Представим, что вопреки нашему утверждению кому-то удалось перенумеровать точки этого отрезка", после чего приводятся хитрые комбинации с нумерацией. Но здесь следует напомнить фундаментальный принцип классической логики и классической математики, который постулирует полное отрицание актуальной бесконечности: "Infinitum Actu Non Datur" (Аристотель) - "актуальная бесконечность не существует". Принцип утверждает потенциальный, т.е. принципиально незавершаемый характер бесконечности множества. Актуальная, то есть, пересчитанная бесконечность лишена смысла. Бесконечностью может считаться лишь потенциальная бесконечность, завершить счет членов которой невозможно. Поэтому приводимое доказательство на этих словах можно и прервать - оно некорректно с самого начала. Впрочем, в этом вопросе особое мнение, которое следует признать некорректным, приписывается Давиду Гильберту. По мнению немецкого математика, одного из величайших умов своего времени, главное различие между актуальной и потенциальной бесконечностью заключается в следующем. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность - это завершённое целое, в действительности содержащее бесконечное число предметов [5].

В литературе можно встретить описание довольно интересного способа подсчета количества точек на отрезке линии. Нетрудно догадаться, что в этом примере использованная методика счета ошибочна и ведет к ошибочному выводу. Несложное доказательство несчетности содержит не очень сильно скрытую подмену понятий. Итак:

"Теперь уже несложно доказать, что множество всех точек на прямой линии несчетно. Вместо этого множества можно говорить о множестве всех действительных чисел, так как каждой точке прямой соответствует действительное число и обратно. Каждое действительное число можно записать в виде бесконечной десятичной дроби вида α, α₁ α₂ α₃ ... α_n..." [3, с.73-74].

Как видим, ряд знаков имеет бесконечное счетное количество знаков и, резонно предположим, что так же считает и автор доказательства. Сразу же заметим, что утверждения следует признать абсурдными. Любое конечное число всегда меньше бесконечности.

"Предположим, что нам удалось каким-то образом перенумеровать все действительные числа. Чтобы доказать, что это предположение неверно, достаточно построить хоть одно незанумерованное число. ... поступим следующим образом. Сначала напишем нуль и поставим после него запятую. Потом возьмем число, получившее первый номер, и посмотрим на его первый десятичный знак после запятой (то есть на число десятых)" [там же].

Для определенности отметим, что поиск незанумерованного числа производится, как можно заметить, на отдельном интервале всех действительных чисел [0, 1]. Сначала как на неточность в этом рассуждении, как и в предыдущем доказательстве, сразу же укажем на очевидное, но, похоже, незамеченное обстоятельство: на самом деле при последовательном, возрастающем счёте у второго числа вторая цифра тоже будет 0. И у третьего. И у четвертого. И у числа, занимающего бесконечно большую позицию. На словах это, возможно, не совсем ясно, поэтому покажем это на "виновнике торжества" - на оцифрованном отрезке:

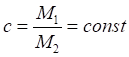
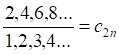
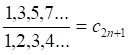
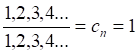
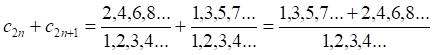
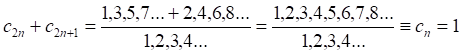
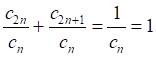
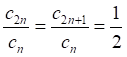
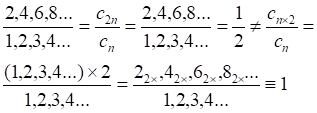
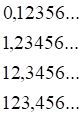kantor

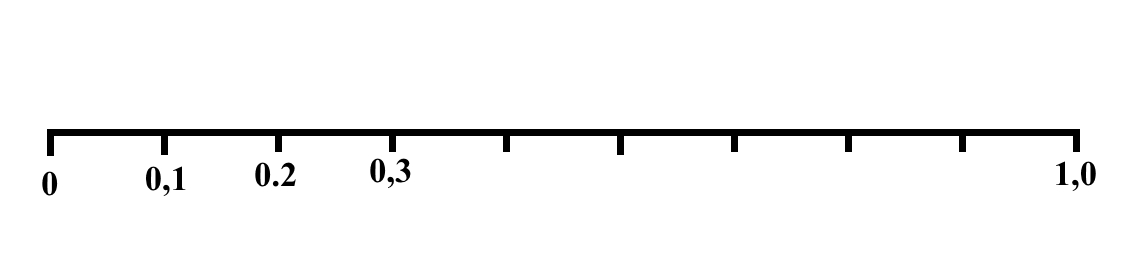
Рис.1. Оцифрованный отрезок, отдельный интервал всех действительных чисел

На рисунке видно, что первая цифра после нуля будет отличной от нуля, единица будет только после точки 0,1 отрезка. На интервале от 0 до 0,1 содержится счетное (пока оспариваемое) количество точек. Во всяком случае, это не одна, не миллион и даже не гугл точек, равный 10¹⁰⁰, а в бесконечное число раз больше. У всех этих чисел первой цифрой после запятой будет ноль. Следовательно, искомое число пока находится вблизи нулевой точки, в самом начале отрезка [0, 1].

"Если эта цифра отлична от 1, то в числе, которое мы пишем, поставим после запятой 1, а если эта цифра равна 1, то поставим после запятой 2" [3, с.73-74].

Еще раз отметим, что отличная от единицы цифра в первой позиции после нуля первого числа будет нулем. Следовательно, в "искомом" числе после запятой первой будет 2. То есть, число будет 0,2. Сразу же на рисунке находим, что эта точка на отрезке есть - это точка 0,2.

"Затем перейдем к числу, получившему второй номер, и посмотрим на его вторую цифру после запятой. Снова если эта цифра отлична от единицы, то в числе, которое мы пишем, поставим на месте сотых цифру 1, если же эта цифра является единицей, то поставим цифру 2" [там же].

Как и в предыдущем случае, вторым знаком опять будет ноль, поскольку точки расположены рядом и их номера различаются лишь в очень далекой позиции после нуля. Следовательно, и вторая цифра искомого числа будет 2. То есть, это будет число 0,22. По рисунку видно, что и эта точка на отрезке имеется. Она находится правее точки 0,2 и отстоит от неё примерно на 1/5 отрезка от 0,2 до 0,3.

"Точно так же будем действовать и дальше, каждый раз обращая внимание лишь на n-ю цифру числа, получившего n-й номер. В результате мы выпишем некоторое число, например, N=0,1121211. . . [там же].

Но мы уже можем заметить, что такое число не получается. А получится число 0,22222..., в котором цифра 1 появится очень и очень не скоро. И эта цифра, единица также будет тиражироваться многократно. В конечном счете, формируемое число примет вид:

N=0,22222...11111...22222...11111

Кстати, можно догадаться по алгоритму, что число будет в основном состоять из двоек, поскольку из 10 цифр единица, которую помечаем двойкой, только одна.

"Ясно, что это число не получило никакого номера: в первом десятичном знаке оно отличается от числа с номером 1, во втором -- от числа с номером 2, . . ., в n-м -- от числа с номером n и т. д." [3, с.73-74].

Верно это только отчасти, поскольку в целом неверно. Указанные совпадения, действительно, на первом участке отрезка отсутствуют. Однако это найденное число совпадает в первом знаке с бесконечным множеством чисел, соответствующих другой точке отрезка - [0.2, 0.3]. Первым и вторым знаками оно соответствует множеству чисел следующих точек этого отрезка. Первым, вторым и третьим - следующему множеству точек отрезка. И так далее - до бесконечности! Проще говоря, "найденное" число будет находиться правее числа 0,222 и бесконечно близко к нему, никогда не достигая числа 0,223.

"Чтобы читателю стало яснее, как выписывается число, не получившее номера, предположим, что при выбранной нумерации первые пять чисел имеют следующий вид:

4,27364...

--1,31226...

7,95471...

0,62419...

8,56280... " [там же].

Здесь очевидна небольшая неточность, поскольку автором, судя по всему, выбран интервал [0, 1], а на этом интервале таких чисел при выбранной нумерации не будет никогда. Однако эту неточность оставим без критики, просто заменив в них цифру перед запятой на ноль, поскольку пояснение вполне верно описывает принцип формирования искомого числа.

"Тогда число, не получившее номера, будет начинаться со следующих десятичных знаков: 0,12121 . . . Разумеется, не только это, но и многие другие числа не получили номеров (мы могли бы заменять все цифры, кроме 2, на 2, а цифру 2 на 7 или выбрать еще какое-нибудь правило). Но нам достаточно существования одного-единственного числа, не получившего номера, чтобы опровергнуть гипотезу о возможности нумерации всех действительных чисел" [3, с.73-74].

Еще раз отметим, что доказательство на самом деле рассматривает бесконечно малую часть всех действительных чисел - на интервале [0, 1]. Предложенный способ просмотра чисел некорректен. При таком способе все просматриваемые действительные числа на этом интервале будут сгруппированы возле нулевой точки. И ожидаемого числа 0,12121, приведенного в качестве примера, получено не будет никогда. А будет образовано указанное выше число N из бесконечного количества двоек.

Следовательно, в этом отношении доказательство не может достичь успеха, поскольку полученное число точно имеется на близлежащем интервале. Действительно, на интервале, например, от 0,222 до 0,223 присутствуют все возможные комбинации знаков после запятой, в том числе и знаков указанного числа N.

Конечно, в доказательстве явно не указана последовательность номеров чисел. Но под "нам удалось" тоже явно никто не указан. Эти самые "нам" могли перенумеровать числа интервала подряд: сначала все возле нуля, затем они дошли до 0,1 и так далее.

В рассмотренном выше примере с перестановкой запятой (2) такие пропущенные числа очевидны, например, в нем отсутствуют числа 1,111 и 2,222. Однако и традиционный метод нахождения пропущенного числа изначально содержит логическую ошибку, противоречие. Подбор такого числа дает результат, который изначально обязательно должен был быть подсчитанным, пронумерованным натуральным числом. Покажем эту очевидную логическую ошибку такого нахождения отсутствующего числа в более явном виде.

Предположим, что в процессе поиска получено новое число, скажем, 0,7182814159.... Однако это число не является новым, отсутствующим в пронумерованном множестве. Это странным образом не замеченное очевидное обстоятельство. Очевидно, что последовательности цифр после запятой всех действительных чисел являются полными, исчерпывающими, содержащими все без исключения их возможные комбинации. То есть, любая наперед заданная комбинация цифр, в том числе и у этого "найденного", обязательно присутствует в бесконечном множестве действительных чисел. Более того, любое число с конечным числом знаков как фрагмент, шаблон присутствует в этом ряду бесконечное число раз. Действительно, "найденных" чисел вида 0,718nnn... - бесконечное множество, как и чисел 0,7182814nnn..., где n - любая цифра, поэтому среди них обязательно имеется и "найденное". Следовательно, любое найденное подобным образом число, обязательно имеется среди подсчитанных, то есть, оно пронумеровано, как и любое другое из множества действительных чисел, что означает счетность всех действительных чисел.

Ошибочность доказательств многих тезисов Кантора вызвана выбором специфического метода подсчета числа элементов, неудачного способа записи последовательностей этих элементов, в результате чего отождествление элементов оказалось завуалированным.

Очевидно, что указанный метод доказательства несчетности множества действительных чисел, который можно назвать традиционным, содержит явную логическую ошибку и непригоден сам по себе. Этот метод опирается на недопустимое предположение "если кому-то удалось все их пересчитать, то можно найти пропущенное". Вместе с тем существует достаточно очевидный способ записи элементов континуума, наглядно доказывающий счетность всех мыслимых видов чисел, и позволяющий записать все их строго последовательно.

Покажем это на примере способа записи всех действительные числа, меньших нуля. Способ записи достаточно очевиден: нужно просто записывать после запятой все последовательные натуральные числа в обратном порядке, инверсно "задом наперед".

Например, под номером 12345678 будет записано действительное число 0,87654321, а инверсией последовательных натуральных чисел 996, 997, 998, 999, 1000 будет создан фрагмент последовательности действительных чисел:

0,699→0,799→0,899→0,999→0,0001 и так далее.

Такая инверсная запись дробной части чисел, меньших единицы, позволяет записать всю их непрерывную, бесконечную последовательность. Инверсная запись, "задом наперед" используется для того, чтобы при возрастании номера сохранялись значащие нули, поскольку при обычной записи будут пропущены, например, действительные числа, имеющие нули сразу после запятой. Очевидно, что бесконечная последовательность содержит все без исключения действительные числа, меньшие нуля, в частности, полную дробную часть π (3,14159...), числа Эйлера - е (2,71828...), основания натуральных логарифмов, константу пропорциональности Ландау - Рамануджана С (0,76422...) и постоянную тонкой структуры α ≈ 1/137, причем с бесконечной точностью. Для удобства эти дробные числа с нулевой целой частью можно представить, например, записью следующего вида:

(3)

где индекс 0 означает, что все числа этого множества не превышают единицы, то есть, перед запятой у них записан 0, а n со стрелкой влево над ним - это обычное натуральное число, записанное после запятой в обратном порядке, "задом наперед", как дробная часть этого элемента множества. Очевидно, это число n является порядковым номером соответствующего элемента множества M₀, точки линии.

Теперь возьмем отрезок, линию [0,1] и отождествим каждую точку этой линии с полученной числовой последовательностью (3). Очевидно, что каждая точка отрезка будет единственно отождествлена с единственным числом последовательности, парно. Ни одна точка или число не будут пропущены. Какое бы число мы ни взяли, на линии обязательно будет точка с таким же значением. Наоборот, какую бы мы не взяли точку на линии, этот номер обязательно будет в созданном массиве. Иначе говоря, рассмотренный отрезок числовой прямой [0, 1], континуум оказывается в биективном соответствии со всеми числами созданного множества.

Собственно процесс нумерации элементов массива или точек линии также достаточно очевиден. В этом процессе, как можно обнаружить, точки, элементы линии, числа сформированного ряда, матрицы оказываются расположенными не в виде монотонной последовательности, а "вперемешку".

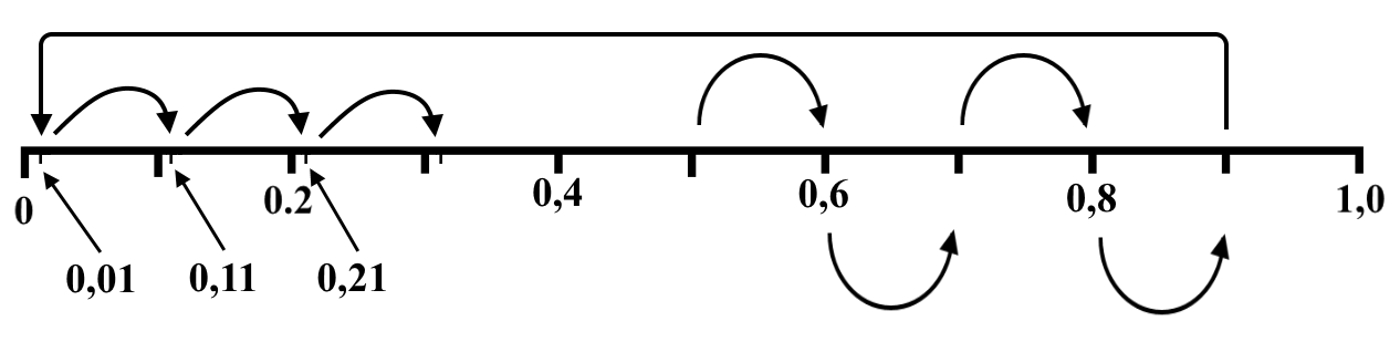
kantor

Рис.2. Нумерация точек отрезка

На рисунке показан фрагмент последовательной нумерации точек, начиная с точки 0,5 и заканчивая на точке 0,31. Мы последовательно рассматриваем фрагмент, точки с натуральными порядковыми номерами 5, 6, 7, 8, 9, 10, 11, 12, 13, по которым из выражения (3) определяем значения этих точек: 0,5 (точка номер 5); 0,6 (точка номер 6); 0,7 (точка номер 7 и так далее); 0,8; 0,9; 0,01 (точка номер 10); 0,11; 0,21; 0,31 (точка номер 13). Как видим, порядковые номера точек равномерно возрастают, но сами точки при этом "скачут" по линии. Отметим главное: фактическое значение точки "возникает" в самом процессе нумерации. То есть, сначала мы выбираем некоторый или очередной, натуральный порядковый номер точки, а затем определяем её местоположение на линии и присваиваем этой точке выбранный номер.

Собственно говоря, нумерация элементов массива и означает присвоение конкретному элементу некоторого определенного номера, как бы навешивание на элемент таблички с номером. Поэтому выбрав элемент, мы можем увидеть его номер, а выбрав номер, узнать, какому элементу он принадлежит. В рассмотренном случае с нумерацией точек линии натуральный порядковый номер, например, 12 389 принадлежит точке на линии со значением 0,98321. Наоборот, точка линии со значением, например, 0,5612999 имеет в массиве порядковый номер 9 992 165.

Такой же алгоритм можно использовать и для нумерации точек плоских или объемных, многомерных объектов, например, точек куба. В случае многомерных объектов номер преобразуется к виду (3) по методу Кантора, созданного им для отождествления точек линии и квадрата [3, с.77].

Предположим, некая точка куба имеет следующие координаты, в которых буквы α, β и γ обозначают любую цифру в этих числах:

kantor (4)

Используя метод Кантора, формируем из этих чисел новое число:

(5)

Отсутствующие цифры для какого-либо индекса заменяем нулями. Дробную часть полученного комбинированного числа инвертируем, поворачиваем "задом наперед", согласно (3), и получаем натуральный порядковый номер рассмотренной точки куба. Например, точка куба с координатами p(x, y, z) = (0,123; 0,321; 0,9171) при комбинировании даст число N=139 221 317 001, что означает порядковый номер точки в бесконечном их массиве, равный 100 713 122 931. Понятно, что обратным преобразованием можно так же найти координаты любой точки по её номеру. Например, точка с порядковым номером 1 234 567 890 имеет в кубе координаты p(0,0741; 0,963; 0,852). Рассмотренный вариант относится к кубу с единичным ребром, но он может быть легко расширен на куб с любым размером ребра, а также на объекты вообще с любым числом измерений.

Наконец, метод позволяет перенумеровать и составные элементы: комплексные числа, кватернионы и тому подобные. Например, комплексное число можно представить в виде

В этой записи буквами α и γ обозначены целая часть числа реальной и мнимой части, а буквами β и δ, соответственно, их дробные части. Например:

Количество цифр α, β, γ и δ в записях может быть любым. Теперь, используя метод комбинации, можно получить число N, инверсная запись которого и будет обозначать натуральный порядковый номер этого числа в их бесконечном массиве. Например, приведенное выше комплексное число будет иметь в бесконечном массиве всех возможных комплексных чисел натуральный порядковый номер 200 123 021 325. Кстати, можно заметить, что в таком массиве первые 10 чисел (0...9) являются реальными, а число i (комплексная единица) находится на позиции 100 и имеет порядковый номер 10. Также заметим, что при таком подходе основой всех чисел являются вещественные числа, а различные комплексные и им подобные - это простая комбинация этих базовых чисел. Условно говоря - все эти комбинационные числа являются своеобразной тенью, миражом чисел реальных.

Нетрудно заметить, что нумерация комплексных чисел тождественна нумерации точек квадрата. В этих частных случаях можно легко применить для их нумерации традиционный диагональный процесс Кантора.

Далее, если составить множество строк, подобных выражению (3), в каждой из которых вместо нуля теперь уже будут записываться последовательные натуральные числа, то образуется квадратная таблица, матрица, содержащая все без исключения положительные действительные числа. То есть, запись (3) будет иметь следующую расширенную форму:

(6)

где x, y - это обычные натуральные числа, которые, как и выше, записаны в обратном порядке, "задом наперед", что обозначено обратными стрелками над ними. Нетрудно догадаться, что эти числа могут обозначать соответствующие координаты точек квадрата.

Дублирование строк со знаком минус добавит в таблицу и все отрицательные действительные числа. Если теперь записать матрицу координат его точек по выражению (5) для их подсчета диагональным процессом Кантора [3, с.70], то полученная запись будет иметь вид:

0,0→0,1→0,2→0,3→0,4→... →0,0001 и так далее.

1,0→1,1→1,2→1,3→1,4→... →1,0001 и так далее.

2,0→2,1→2,2→2,3→2,4→... →2,0001 и так далее.

3,0→3,1→3,2→3,3→3,4→... →3,0001 и так далее.

...

10,0→10,1→10,2→10,3→10,4→... →10,0001 и так далее.

Нетрудно заметить, что такая запись содержит весь бесконечный ряд действительных чисел, причем слева (столбцом) и справа от запятой записаны независимые ряды в диапазонах значений от 0 до 1. Понятно, что ряд слева от запятой нужно читать справа налево, добавив в начале него 0 и запятую.

Такая трактовка этих последовательных числовых рядов позволяет присвоить значения их членов координатам точек квадрата, присвоить каждую пару этих чисел x, y каждой из точек квадрата со стороной 1 - без взаимных пропусков, то есть, обеспечить их полное биективное соответствие. Действительно, каждая точка квадрата на его некоторой, например, горизонтальной линии может быть пронумерована, как и точки линии, дробной частью x чисел представленного квадратного массива. Соответственно, каждой линии по вертикали так же может быть присвоен номер y, записанный инверсно, "задом наперед", то есть, и всё бесконечное множество горизонтальных линий квадрата будет пронумеровано всем рядом действительных чисел, меньших единицы. Теперь все точки квадрата в созданной матрице можно пересчитать диагональным процессом Кантора. Причем, отчетливо видно, что в представленной матрице первая строка номеров точек квадрата тождественна строке номеров точек линии (3) при y = 0. А это означает, что количество точек на линии в бесконечное число раз меньше количества точек на квадрате.

Следует признать, что нумерация точек квадрата диагональным процессом менее удобна, чем способ конвертации номеров (6). При конвертации мы легко можем по натуральному порядковому номеру N точки p(x,y) определить её координаты x, y и наоборот. Использование же в этих целях выражения (5) связано с заметными вычислительными трудностями.

Таким образом, приведенные рассуждения позволяют подвести итог и сделать однозначный вывод:

Вся бесконечная последовательность действительных чисел, континуум любого числа измерений являются счётными, все они могут быть пронумерованы натуральными числами.

Задача об "Отеле Гильберта"

Судя по всему, вопросы бесконечных множеств сложны не только для рядовых математиков. Иной раз в слабом их понимании можно заподозрить и величайших специалистов в этой области. Рассмотрим рассказ, который, как считается, предложил Гильберт где-то в третьем десятилетии 20 века [9, 8, 10; 3, с.70-71].

Представим себе гостиницу с бесконечным числом комнат. Комнаты пронумерованы натуральными числами от 1 до ∞. Однажды в гостиницу вошел человек и попросил снять комнату. К сожалению, для нового гостя не нашлось комнаты, так как отель был полностью заполнен бесконечным числом гостей, и не было ни одного свободного номера. Как предоставить новому гостю свободную комнату, не выселяя никого из постояльцев?

Несмотря на то, что по условиям задачи все номера заняты, утверждается, что, тем не менее, существует возможность выделить сколько угодно свободных комнат. Для этого необходимо переселить постояльца из первой комнату во вторую, постояльца из второй комнаты в третью и так далее. То есть, каждого постояльца из комнаты с номером n необходимо переселить в комнату с номером n+1, n→n+1. В результате этого освобождается комната с номером один, и в неё можно поселить нового гостя. Здесь неявно подразумевается, что переселение выселением не является.

Но это решение ошибочно. По условиям задачи определённо сказано, что свободных номеров нет! Следовательно, данный "парадокс" Гильберта является псевдо парадоксом [9], поскольку вместо подселения производится выселение. В предложенном решении производится подмена понятий. Состояние, стационарное, неизменное - заполненность всех номеров жильцами - подменяется процессом, динамическим, движением - переселением постояльцев из одного номера в другой.

Во-первых, этот процесс будет длиться вечно, во-вторых, в случае даже одного нового гостя, на всём протяжении процесса переселений один из постояльцев всегда будет без гостиничного номера, то есть, будет сидеть в коридоре, что является нарушением условий решения задачи. Иначе говоря, все постояльцы просто поделились своим временем проживания с новым жильцом как в пословице "с миру - по нитке".

Собственно математическая ошибка состоит в том, что за большим числом постояльцев как-то незаметно прячется суть задачи. Математической процедурой, манипуляцией с бесконечностями подменяется само содержание исходного тезиса: подселение в заполненный отель дополнительных постояльцев. Показать эту подмену можно, если взять противоположный предельный вариант: в отеле всего один номер, и он занят. Для того чтобы поселить нового, прежнего постояльца временно выселяют буквально в коридор под предлогом переселения. Здесь, как видим, и обнаруживается скрытая подмена понятий переселения и выселения. Вновь пришедшего гостя селят в освободившийся номер. Но прежнего постояльца тоже надо куда-то поместить. Поэтому вновь заселенного гостя опять выселяют, а на его место селят прежнего постояльца. И так по кругу. В конечном счете, каждый из них в номере проживает только половину времени, а вторую - на стуле в коридоре.

В таком варианте задача принципиально ничем не отличается от задачи с бесконечным числом комнат. Добавим ещё одну комнату и будем по кругу переселять теперь уже троих постояльцев. Можно добавить и четверную комнату и производить всё ту же процедуру "переселения-выселения". Дойдя до бесконечности, мы и получим парадокс отеля в исходном варианте. Однако в его минимальной конфигурации мы явно обнаруживаем: постояльцы, по сути, часть времени проводят на стуле возле комнаты. При бесконечном числе комнат и конечном числе новых постояльцев это время стремится к нулю. Отличие только в этом. Если же число постояльцев растет, как предлагается в расширенных версиях парадокса, то и время "на стуле около комнаты" также будет расти вплоть до той же исходной величины - половины времени проживания. Рассмотренные решения "парадоксов" нарушают главный принцип отелей: постоялец должен вселиться и жить в нем, пока сам не решит его покинуть.

Вместе с тем, обнаруженное нарушение можно отнести к слабому опровержению решения задачи. Более важным выводом из неё является заявленное доказательство несчетности всех действительных чисел. Но ошибочно и это доказательство.

Несостоявшаяся перепись

Парадокс отеля оказался настолько интересным и показательным, что он получил дальнейшее развитие, которое описано, например, в виде шутливого научно-фантастического рассказа от имени вымышленного персонажа:

"Из треста космических гостиниц пришел приказ составить заранее все возможные варианты заполнения номеров. Эти варианты потребовали представить в виде таблицы, каждая строка которой изображала бы один из вариантов. При этом заполненные номера должны были изображаться единицами, а пустые нулями. Например, вариант 101010101010... означал, что все нечетные номера заняты, а все четные пустые, вариант 11111111111... означал заполнение всей гостиницы, а вариант 000000000000... означал полный финансовый крах -- все номера пустовали" [9, с.70-71].

Этот фрагмент, цитата является продолжением рассказа об "Отеле Гильберта", для случая бесконечного числа отелей с бесконечным числом номеров и бесконечным множеством гостей. В продолжении рассмотрен еще один из вероятных парадоксов, возникающих в таком тресте отелей. Итак, форма отчета определена. Далее определяется способ его составления:

"Директор был перегружен работой и поэтому придумал простой выход из положения. Каждой дежурной по этажу было поручено составить столько вариантов заполнения, сколько номеров было в ее ведении. При этом были приняты меры, чтобы варианты не повторялись. Через несколько дней списки были представлены директору, и он объединил их в один список" [там же]

К сожалению, способ описан недостаточно четко, например, что представляют собой "принятые меры", поэтому с учетом предыдущей информации из книги проясним некоторые детали. Фраза определённо противоречива. Изначально под вариантом подразумевалось одно единственное двоичное число, каждый разряд которого относится только к одной комнате. Если же дежурный составляет много вариантов, то неясно, чем они могут отличаться друг от друга? Вернее, ясно, что все они - это один и тот же вариант, одно и то же число с битами - признаками занятости номеров. В дальнейшем же под вариантом явно подразумевается номер той или иной комнаты на этаже.

На каждом этаже у дежурной по определению должно быть бесконечное, счетное количество номеров. В противном случае вариантов в смысле номеров комнат у неё будет конечное количество, то есть, каждое двоичное число будет иметь вполне определенное число знаков. Например, 10¹⁶⁵ нулей и единиц. В этом случае задача имеет однозначное решение при бесконечном количестве гостиниц и этажей, поскольку любая счетная (потенциальная) бесконечность перекрывает любое конечное число вариантов.

Но, с другой стороны, если на этаже счетное, то есть, бесконечное количество номеров, то и в этом случае будет получен список вариантов, содержащий все возможные комбинации из бесконечного (счетного) числа нулей и единиц. То есть, и в этом случае задача решается однозначно, то есть, список вариантов будет единственным и полным.

"-- Могу ручаться, что список неполон. Я берусь указать вариант, который наверняка пропущен" [3, с.70-71].

Вполне ожидаема подмена понятий, но её следует показать непосредственно, явно.

"Мы заключили пари. Чтобы выиграть его, я предложил прибить каждый вариант на дверь того номера, которому он соответствовал..." [там же].

Сразу же возразим. Напомним читателю, что вариантов составлено столько, сколько номеров на этаже, а не в гостинице целиком. Список отсортирован по возрастанию, но это не имеет принципиального значения, поэтому просто отбросим варианты других этажей, поскольку и одного этажа окажется вполне достаточно.

"А потом я поступил очень просто. Подойдя к двери первого номера, я увидел, что соответствующий вариант начинается с цифры 0. Немедленно в блокноте появилась цифра 1; это и была первая цифра варианта, который мне хотелось составить" [там же].

Здесь заметна некоторая неопределенность. Гостиниц - бесконечное число (счетное). Можно также предположить, что, соответственно, этажей и комнат на каждом этаже также счетное (потенциально бесконечное) множество. В этом случае смысл первого номера становится неясен. Нумерация ведётся сквозная? Или в каждой гостинице есть свой первый номер? С этажами тоже не совсем ясно, хотя и проще, поскольку по принятой практике первая цифра номера комнаты равна номеру этажа. И вновь примем решение в пользу рассказчика: отбросим все номера кроме номеров на единственном этаже единственной гостиницы, а в номере комнаты отбросим цифры этажа. Следовательно, на каждом этаже каждой гостиницы будет комната с номером 0, причём под "вариантом", очевидно, подразумевается именно номер комнаты.

"Когда я подошел к двери второго номера, то первая цифра соответствующего варианта меня не интересовала, ведь первая цифра моего варианта была уже написана. Поэтому все внимание было обращено на вторую цифру. Увидев, что эта цифра 1, я записал в своем блокноте цифру 0. Точно так же, обнаружив, что третья цифра варианта, прибитого к двери третьего номера, тоже 1, я записал в блокноте цифру 0. Вообще, если я обнаруживал, что n-я цифра n-го варианта есть 0, то писал в своем блокноте на n-ом месте цифру 1, если же n-я цифра n-го варианта была 1, то я писал у себя 0. Когда я обошел все номера гостиницы, то в блокноте оказалась записанной последовательность нулей и единиц" [3, с.70-71].

Методика понятна и разумна, но верные ли выводы из неё делает рассказчик?

"-- Вот, полюбуйтесь на пропущенный вариант.

-- А откуда известно, что он пропущен?

-- Он не может быть первым, так как отличается от него первой цифрой, не может быть вторым, так как отличается от него второй цифрой, третьим, так как отличается от него третьей цифрой, и вообще n-м, так как отличается от него n-й цифрой" [там же].

Как видим, метод полностью совпадает с рассмотренным выше, поэтому также ведет к неверному выводу. В его списке номер начинается, например, с цифры 0. Но это всего-навсего первый разряд бинарного числа бесконечной длины. Можно уверенно заявить, что вся монотонная бесконечная последовательность нулей и единиц в точности содержит половину начинающихся с нуля. Например, пятизначное двоичное число:

00000, 00001, 00010, 00011, 00100 и так далее

содержит всего 32 числа, первые 16 из которых начинаются с нуля. Следовательно, если номер первой комнаты начинается с нуля, то номер второй комнаты тоже будет начинаться с нуля. И так на бесконечном количестве дверей. Поэтому в блокноте вторая цифра, как и первая, так же будет единицей. И третья. И четвертая. И так до бесконечности. Счетной.

Но как же так?! Получается, что все комнаты будут иметь один и тот же нулевой номер?! Нет, разумеется. Просто длина последовательности нулей и единиц такова, что прочитать последнюю цифру рассказчику не удастся никогда. Вернее, за бесконечное (счетное) количество времени.

"... стало ясно, что какое бы счетное множество вариантов ни взять, всегда найдется вариант, не вошедший в это множество... А это и значит, что множество всех вариантов заполнения гостиницы несчетно..." [3, с.70-71].

Как видим, вывод о несчетности вариантов явно ошибочен. Похоже, что этого не заметили и программисты или математики в тресте космических гостиниц, которые обязаны были предостеречь руководство от такого тривиального, бессмысленного задания. Бесконечное (счетное) число вариантов бинарных чисел даёт весь натуральный бинарный ряд чисел. Без пропусков и повторов. Каждый дежурный по этажу должен был составить список всех вариантов (то есть, номеров комнат) из бесконечной последовательности бинарных чисел. Неважно, что дежурных много, а гостиниц - вообще бесконечное (счетное) количество. Каждый из дежурных предоставит в точности один и тот же список вариантов (номеров).

По поводу "отсутствующего" номера комнаты добавим - этот номер в списке есть, но находится среди номеров второй половины бесконечного их количества. Заметим, что при таком способе "нахождения" не проходит и хитрость с отбрасыванием ведущих нулей, то есть:

0, 1, 10, 11, 110, 111, 1110, 1111, 11110 и так далее,

поскольку в этом случае у второй комнаты в номере отсутствует вторая цифра, у третьей - третья, у четвертой - четвертая и так далее.

Разрядность и количество чисел в массиве

Легко показать, что причина ошибки заключается в том, что при поиске отсутствующего числа по непонятной причине количество разрядов чисел (записей в блокноте) приравнивалось общему количеству всех чисел. В сущности, это очевидное и даже тривиальное некорректное допущение, и почему оно оказалось незамеченным, непонятно. Действительно, общее количество чисел, их основание и разрядность связаны простым соотношением

(7)

где

k - количество чисел разрядности n и основанием m;

m - основание чисел: десятичные, двоичные и т.д.;

n - разрядность чисел, числового ряда.

Например, общее количество чисел с основанием 10 (десятичные) и разрядностью 5 равно 100 000, то есть, от 00000 до 99 999. А количество чисел с основанием 2 (бинарных) и числом разрядов 16, соответственно, равно 2¹⁶ - или 65 536 чисел от 0000 0000 0000 0000 до 1111 1111 1111 1111. Точно такие же соотношения можно составить и для любых других оснований - шестнадцатеричного, восьмеричного и так далее.

Рассмотрим массив бинарных чисел, использованных в "блокнотном методе", и возможность метода определить число, номер, не использованный при нумерации комнат. Сначала вновь обратимся к примеру с массивом пятизначных чисел, теперь уже двоичных, бинарных.

Обобщённо в двоичном коде пятизначное число можно записать как nnnnn c диапазоном от 00000 до 11111. Количество этих чисел равно 2⁵ = 32. Поскольку их относительно мало, можем записать все их в виде таблицы 4х8 - слева направо, сверху вниз:

kantor

Теперь можно воспользоваться "блокнотным методом". Рассказчик и его герой в рассказе, а также все их последователи искали пропущенное число поразрядно, то есть, переходя от двери к двери комнат отеля, добавляли к записи в блокноте всё новый и новый разряд, полагая, что тем самым они просмотрели все возможные числа, номера комнат. Но на самом деле, как видно из соотношения, они переберут только количество чисел, равное их разрядности.

Мы, согласно традиции метода, предполагаем, что кому-то удалось пересчитать и перенумеровать все 32 числа в этой таблице. Попробуем доказать, что счётчик всё-таки пропустил, по меньшей мере, одно число. Итак, смотрим на первое число. Его первый разряд равен нулю, поэтому записываем в блокнот единицу: 1nnnn. Остальные четыре цифры нам пока неизвестны. Теперь смотрим на второе число, двигаясь по таблице сверху вниз. Видим, что вторая цифра второго числа равна единице, поэтому записываем в блокнот цифру 0 вторым разрядом нашего числа: 10nnn. Смотрим третье число и видим, что третья цифра равна нулю. Делаем запись в блокнот: 101nn. Таким же образом записываем и четвёртую цифру 1 в блокнот, заметив, что четвёртая цифра четвёртого числа в таблице равна нулю: 1011n. Последнее, пятое число в таблице берём рядом с предыдущим: последнее число в следующей колонке. В результате получаем в блокноте окончательно число 10110. Согласно "блокнотному правилу" наше число отличается от первого первой цифрой, от второго - второй, от третьего - третьей и так далее. Следовательно, мы должны сделать вывод, что счётчик не пронумеровал это число в процессе подсчёта, ведь оно отличается первым разрядом от первого числа... и так далее. Однако... это явно не так. Реально мы просмотрели только 5 (пять) чисел в колонках, хотя общее количество чисел равно 32 - в 6 раз больше. И это, якобы пропущенное число, в этой таблице точно есть. Находится оно в третьей строке в седьмой колонке. Заметим, что порядок просмотра номеров в таблице значения не имеет, просто будут получены разные "пропущенные" номера.

Еще раз отметим, что метод просматривает совсем даже не все числа, а только их количество, равное разрядности числа. Но ведь по условиям рассказа об отелях номеров на этаже - бесконечное количество, то есть, разрядность каждого числа также равна бесконечности. Тем не менее, это ровным счетом ничего не меняет, в этом случае герой рассказа точно так же просмотрит не все числа, а только их часть, и найденное им якобы отсутствующее число обязательно будет присутствовать среди чисел, до которых он просто никогда не дойдёт.

Как говорится, что-то пошло не так. А не так пошло использованное "блокнотное правило". Мы в рассматриваемом общем массиве чисел можем, имеем право просмотреть только 5 (пять!) чисел. Любое следующее число обязало бы нас приписать к "найденному" числу ещё один разряд, но в нашем массиве нет 6-разрядных чисел. Отношение разрядности чисел к их количеству (7) в массиве описывается простым уравнением:

kantor

Здесь n - это основание массива: в нашем случае бинарных чисел m = 2. Для десятичных чисел основание m = 10, для шестнадцатиразрядных hex-чисел m = 16. Соответственно, n - это разрядность чисел, в нашем случае n = 5, следовательно, N ~ 1/6. Используя это уравнение, мы можем определить соотношение N и для других, например, для 10-разрядных бинарных чисел:

kantor

Замечаем, что при увеличении разрядности чисел отношение уменьшается. В пределе, какой рассматривается в задаче об отеле Гильберта, разрядность чисел - номеров комнат в отелях стремится к бесконечности.

kantor

Это означает, что при бесконечном количестве комнат счётчик может просмотреть хотя и бесконечное их количество, но в общем количестве комнат это просмотренное количество эквивалентно нулю.

Получается, что доля просмотренных героем рассказа чисел от общего их количества равна нулю, поэтому нет ничего удивительного, что любое найденное им число обязательно будет присутствовать в их полном наборе. Собственно говоря, это тривиальный, очевидный факт: всё бесконечное множество чисел бесконечной разрядности содержит все возможные числа, то есть, это тождественно весь натуральный ряд чисел, поэтому "отсутствующих" чисел в нём быть не может просто по определению.

Такой же результат будет получен, если рассматривать не разрядность, а общее количество чисел.

kantor

Следовательно, каким бы большим ни был найденный им номер комнаты, якобы не получившей порядкового номера, номера всех комнат используют все без исключения числа от нуля до бесконечности, то есть, содержать все возможные порядковые номера, среди которых обязательно присутствует и "пропущенный" номер.

Таким образом, вывод о несчетности вариантов, номеров комнат является ошибочным. Похоже, что и в управлении космических гостиниц тоже не нашлось грамотного программиста или математика, которые могли бы объяснить директору ошибочность вывода о неполноте списка, и что пари выиграл именно он, директор.

Счетность всех мыслимых видов чисел

Теперь еще раз обратимся к утверждению о несчетности континуума. Действительные числа являются лишь частью ряда возможных чисел, включающих в себя вещественные, комплексные, кватернионы, гиперкомплексные, поличисла (коммутативно-ассоциативные гиперкомплексные числа), разнообразные многомерные и любые иные виды чисел. Здесь нас не должны интересовать алгебры этих чисел и их свойства. Единственное не обязательное условие - это конечная длина записи числа. То есть, запись числа в виде бесконечного ряда коэффициентов мы пока оставим без внимания, указав, что задача решается так же - предельным переходом.

Все мыслимые числа в общем виде можно записать, например, в следующем виде

где

α - любое вещественное число;

С - любой индекс, например, мнимая единица i.

Например, число может иметь вид a = 2,71828... -действительное число, или a = 3+2i - комплексное число, или a = 5+2i+3j+8k - кватернион. Правильно организованный способ подсчета этих чисел позволяет показать счетность всего их ряда. Вообще-то, такой результат является простым следствием принятого способа подсчета. На классический вопрос "сколько будет дважды два?" известен шутливый ответ: а сколько надо? По большому счету, всё сводится к спору о том, какой способ подсчета лучше или правильнее. Рассмотрим следующий способ записи всех действительных чисел: запишем после запятой все последовательные натуральные числа "задом наперед", а до запятой - в каждом ряду возрастающие натуральные числа на всём числовом диапазоне. Возникает, например, такой фрагмент последовательности действительных чисел:

0,699→0,799→0,899→0,999→0,0001 и так далее.

Последовательность чисел в таблице будет содержать все без исключения числа. Собственно правило формирования чисел имеет простое аналитическое выражение, подобное (3) или (6). Возьмем два натуральных числа m и n, изменяющиеся от 0 до бесконечности. Запишем с их помощью некоторое число в виде

(8)

Здесь запись {0,m} означает число, меньшее единицы, дробной частью которого является натуральное число m. Фактически при табличной записи чисел n является номером строки в таблице, а m - номером колонки. Например, в ячейке (n=3; m=5) будет находиться число:

а в ячейке (n=10; m=2021) будет находиться число

Для составления таблицы начнем перебирать, подсчитывать все получившиеся числа. Строки чисел будут иметь вид:

0,0+0,9+0,8...+0,1+0,90+0,89+0,88...+0,81+0,80+0,79 ... +0,12121...

1,0+1,9+1,8...+1,1+1,90+1,89+1,88...+1,81+1,80+1,79 ... +1,12121...

2,0+2,9+2,8...+2,1+2,90+2,89+2,88...+2,81+2,80+2,79 ... +2,71828...

3,0+3,9+3,8...+3,1+3,90+3,89+3,88...+3,81+3,80+3,79 ... +3,14159...

4,0+4,9+4,8...+4,1+4,90+4,89+4,88...+4,81+4,80+4,79 ... +4,12121...

Знаки плюс в таблице означают не суммирование, а используются как разделитель между числами. В связи с повторами, поскольку числа вида 0,1+0,10+0,100+0,1000 в использованном алгоритме считаются разными, общее количество чисел, видимо, окажется больше примерно на 10%. Конечно, мы можем повторяющиеся числа пропускать, не считать, но 10% погоды не делают. Если изобразить расположение чисел на графике, то график будет иметь вид пилы.

Для большей общности можно добавить еще одно условие: четные числа n будем делить на 2 и полученное число записывать согласно выбранному виду. Для следующего нечетного числа n запишем то же самое число, только со знаком минус. Очевидно, что в такой ряд легко включить и все вещественные и действительные, комплексные числа и даже кватернионы. Нумерация сформированных чисел соответствует нумерации членов любого числового ряда, то есть, каждое число из таблицы получит свой индивидуальный натуральный порядковый номер, будет пронумеровано при подсчёте. Каким бы ни было количество всех действительных чисел, наше движение по ряду не пропустит ни одного из них, и каждое из них получит свой индивидуальный натуральный номер. Таким образом, можно сделать вывод: континуум является счетным. Используя обратный метод индексации Кантора [3, с.77], мы можем корректно включить в этот континуум все мыслимые виды чисел. Как известно, метод Кантора формирует новое число из двух следующим образом:

kantor

У двух рациональных чисел x и y берутся цифры после запятой и поочередно вписываются после запятой третьего числа z. Мы проделаем обратную операцию, сформируем из одного числа несколько коэффициентов, например, для кватерниона. Возьмем из полученного ряда какое-либо число z и будем рассматривать его как составное, отбросив ноль и запятую:

Очевидно, что все составляющие число цифры гарантируют любую комбинацию, поскольку ряд чисел z бесконечен. Теперь составим из одноименных цифр новое число, кватернион:

Здесь в каждом коэффициенте показаны только четыре цифры, но, очевидно, их может быть любое количество. Также очевидно, что и самих коэффициентов может быть любое число: один коэффициент даёт действительное или вещественное число, два коэффициента дают комплексное число и так далее.

Понятно, что полученный ряд всех возможных чисел является счетным, каждое из исходных чисел имеет свой индивидуальный натуральный порядковый номер. Среди этих чисел обязательно окажутся и число е (2,71828...), и π (3,14159...), и константа пропорциональности С (0,76422...) Ландау - Рамануджана, и постоянная тонкой структуры α ≈ 1/137, причем с бесконечной точностью. Счетность ряда обеспечивается использованием метода квадратов, предложенного математиком-филателистом из рассказа об отелях с бесконечным числом номеров [3, с.57] являющегося эквивалентом диагонального процесса Кантора:

kantor

Метод мы будем использовать в точности, как в рассказе, поэтому числа из приведенной выше таблицы расположатся друг за другом и получат соответствующие номера примерно в следующей последовательности:

0,0+0,9+1,9+1,0+0,8+1,8+2,8+2,9+2,0...+0,1+1,1+2,1+3,1+3,8+...

Здесь знак плюс между числами также является простым разделителем, вместо пробела или запятой. Мы приводим только положительные числа, но, как отмечено выше, таблица содержит все вещественные, действительные и прочие числа. Порядок их подсчета соответствует правилу нумерации членов ряда, то есть, каждое число из таблицы получит свой индивидуальный порядковый номер, то есть, будет пронумеровано.

Здесь мы не можем не привести мнение ещё одного исследователя по поводу счетности членов множеств, мнение исследователя, с работой которого мы ознакомились уже после написания данной статьи:

"... мы собираемся доказать, что действительные числа несчетные, значит, иррациональные числа тоже не будут счетными. [12, с.103].

Это утверждение мы называем ошибочным. Для его доказательства цитируемый автор используется тот же метод, что и рассмотренный выше метод для определения непронумерованного номера в отеле Гильберта, то есть, метод некорректный, который по определению не может достичь конца даже конечного множества.

Таким же ошибочным является и следующее утверждение этого же автора:

"... целых чисел..., как и рациональных чисел, не больше, чем натуральных, несмотря на то что так может показаться на первый взгляд" [12, с.98].

Заметим, что все натуральные числа являются целыми по определению, а целые числа - это натуральные с добавлением к ним нуля и отрицательных чисел (Википедия). Следовательно, согласно этим определениям целых числе больше, чем натуральных, а приведённая цитата - ошибочна. Тем не менее, нет никаких противоречий в том, чтобы пересчитать все целые числа, то есть, перенумеровать их натуральными числами, присвоить каждому из них порядковый номер. Проблема счёта отсутствует в связи с невозможностью его завершения. Кроме того, наш метод формирования числовой последовательности включает все мыслимые виды чисел, пересчитать которые позволяет методы Кантора или математика-филателиста.

Признаемся, что дальнейшее чтение работы цитируемого автора мы прекратили, поскольку эти две ошибки ясно показали его позицию, приверженность ошибочным аргументам многих предшественников, аргументам, которые здесь мы подвергли развёрнутому анализу и критике.

О равномощности отрезка и квадрата

К таким же ошибочным выкладкам следует отнести и известное доказательство Кантора равной мощности точек в прямом отрезке и квадрата со стороной, равной этому отрезку. На самом деле мощность множества точек квадрата на отрезке имеет более высокий порядок, чем мощность множества точек отрезка. То есть, больше в бесконечное, счетное число раз.

Есть наглядный и предельно простой способ показать это: нужно отрезок просто наложить на квадрат. Под отрезком окажутся все тождественные ему точки квадрата. Остальные точки квадрата образуют отдельное бесконечное множество точек, очевидно, большей мощности. Если же отрезок длиннее стороны квадрата, то, казалось бы, можно найти такой квадрат, который будет содержать меньше точек, чем эта линия:

"Разумеется, можно разломать прямую линию на отрезки, длина которых равна стороне квадрата, и после этого каждый отрезок поместить в квадрат так, чтобы они не пересекались друг с другом" [3, с.59].

Это верно, но ломать линию совсем не обязательно. В доказательстве Кантора длина линии равна стороне квадрата. Однако, может быть, разлом линии в цитате предложен для того, чтобы завуалировать, спрятать фактическое опровержение этого доказательства? Действительно, если наложить отрезок на квадрат, то их точки будут отождествлены, причем, вопреки Кантору, у квадрата точек окажется несопоставимо больше, чем у линии. Как бы то ни было, в цитате отчетливо просматривается мысль, что линия содержит меньше точек, чем квадрат. По аналогии с таким разбиением возникло и обратное предположение:

"Но вдруг и квадрат можно как-то разбить на части, а потом эти части положить на прямую, чтобы они не задевали друг друга?" [3, с.59].

Алгебраически с учетом равной метрики, как показано выше, это возможно: вытянуть квадрат в линию. Такой способ совмещения, алгебраический сразу же высвечивает противоречивость решения Кантора. К сожалению, автор цитаты не стал развивать эту идею дальше.

Для сравнения двух множеств точек следует попытаться установить однозначное соответствие между этими точками, то есть, показать, что точки обоих этих множеств можно объединить, скажем, в пары (a, b), такие, что каждый элемент, каждая точка a принадлежит линии, а каждый элемент, точка b - квадрату, причем каждый из элементов a и b попал только в одну пару [3, с.59].

Согласно Кантору два бесконечных множества - точки линии и квадрата - имеют одинаковое количество элементов, если между этими элементами можно установить указанное однозначное соответствие. В математике обычно говорят о мощности множества, подразумевая под нею количество его элементов. Следовательно, отрезок и квадрат, построенный на нем, по Кантору имеют одинаковую мощность. Для доказательства этого он использует следующий метод. В системе координат x0y простроен квадрат ABCD, причем точка A совпала с началом координат, а точка B лежит на оси x. Не всякий способ позволяет установить взаимное однозначное соответствие между точками квадрата и отрезка:

"Проектирование точек квадрата на отрезок АВ здесь не помогает, ведь при проектировании в одну точку отрезка перейдет бесконечное множество точек квадрата (например, в точку А -- все точки отрезка DA)" [3, с.77].

Однако такое обоснование нас, разумеется, устроить не может, поскольку это решение верное, но оно все-таки отбрасывается. Координаты каждой точки квадрата можно представить в мнемоническом виде:

kantor

В этих записях каждый символ α, β представляет собой какую-либо цифру из 0...9. То есть, x и y - это просто два дробных числа, меньшие единицы. Здесь следует, кстати, выразить недоумение по поводу отождествления чисел вида 0,50000... и 0,499999....

"...например, 0,500000... и 0,49999999...-- это одно и то же число. Для определенности будем пользоваться записью с нулями" [3, с.73].

В частности, вопрос: отождествляются только такие числа? А, например, числа 0,550000... и 0,549999... не отождествляются по такому же принципу? Это правило, собственно говоря, не выдумка. Например, его использует офисная программа MS Excel, правда, с противоположной "определенностью". Там любое целое число в одном из представлений так и записывается: с множеством девяток в конце. Но в нашем случае мы рассматриваем числа в их абсолютном смысле. Поэтому число 0,5000...1 и число 0,5, число 0,4999999... или даже 0,4999...9998 - это совершенно разные числа. Если же вводить указанное правило (округление), то следовало бы и здесь дать веские обоснования, почему такой участи избежали числа 0,549999... или 0,22229999..... Чем они кардинально отличаются? Если же правило распространить и на них, то сразу же образуется счетная бесконечность чисел, отброшенных в результате безосновательного округления.

Итак, после тривиального преобразования координат точки квадрата в мнемоническую запись, с ними производится манипуляция, которая также не имеет веско аргументированного, рационального смысла. Перетасовыванием знаков двух чисел формируется новое число:

Обратим внимание на следующее интересное замечание и на приведенный далее способ отождествления:

"для простоты мы не берем точки квадрата, лежащие на его сторонах, а берем лишь внутренние точки... Нам надо теперь найти точку Q отрезка АВ, соответствующего точке Т" [3, с.78].

Для "простоты" - это, прямо скажем, - лукавство. Этим упрощением отбрасывается неразрешимое противоречие совпадения линии и стороны квадрата.

Точка T - это точка в квадрате с указанными координатами x и y. Координата точки отрезка выбирается по принципу Q = z. Далее делается ожидаемый вывод: точке T квадрата поставлена в соответствие точка Q отрезка [0, 1]. Следовательно, всем различным точкам квадрата соответствуют разные точки отрезка и тем самым установлено взаимно однозначное соответствие между точками квадрата и точками отрезка. Из этого также делается вывод, что множество точек квадрата имеет такую же мощность (количество), что и множество точек отрезка (их количество).

Такие выводы противоречат не только здравому смыслу, но и логике, поскольку налицо подмена понятий. Сначала обратим внимание на то, что же отождествляется. А отождествляется координата точки отрезка и некоторое комбинационное число, которое вообще-то координатой не является. Действительно, координатой чего мы можем признать сборку - число z? Какое отношение эта комбинация знаков имеет к координатам x, y точки квадрата? Координаты - это два числа (так сказать, две штуки), а z - это одно число (одна штука). По существу, число z является для координат x, y своеобразным индексом. Иными словами, мы здесь отождествили не две точки, а точку и некий индекс. Но индекс чего? Квадрат - это плоская фигура, следовательно, каждая его часть изначально должна рассматриваться как такая же плоская фигура, фигура с площадью. И мы фактически отождествили не две точки, а точку и площадку, бесконечно малый квадрат. Размеры точек на линии и точек, площадок на квадрате разные, хотя и те и те бесконечно малы.

Конечно, для отождествления это не является противоречием. Мы можем, например, отождествить 10 яблок и 10 уток. Или 200 кресел в кинотеатре и 200 зрителей. Но при этом следует помнить, что равны не они сами по себе, а их количества. В доказательстве Кантора, вроде бы, так и говорится, что равны мощности, равны количества. Однако преподносится это так, что создается впечатление, будто эти сравниваемые множества равны не только по своим количествам, мощности, но и равны буквально - точка на линии тождественно равна точке на квадрате. При таком подходе можно отождествить любые бесконечности, просто отбросив их качество и оставив лишь безликое количество. Все зависит только от искусства отождествителя. Приведём простой пример.

Точки любой линии на плоскости характеризуются двумя координатами. Точно так же и в рассмотренном примере все точки линии имеют две координаты, одна из которых просто равна нулю. Теперь становится ясным, почему мы обратили внимание на замечание "для простоты мы не берем". На самом деле в таком упрощении преследовалась цель упростить организацию подмены понятий. Ведь если у линии признать наличие имеющейся на самом деле второй координаты, то и для неё пришлось бы также формировать комбинированное число - индекс. Действительно, если вернуть в рассмотрение и стороны квадрата, то одна из них совпадет с отождествляемой линией. В этом случае надо было бы веско обосновать, почему координаты нижней стороны квадрата преобразуются в число z, а линия, полностью совпадающая с этой стороной, по-прежнему описывается одной координатой, хотя у неё однозначно имеется и вторая, нулевая?

Ясно, что разумные обоснования этого просто невозможны. Если же вернуть линии её законные права на вторую, нулевую координату, то все её собственные числа z будут начинаться с нулевого знака. То есть, с линией можно будет отождествить только одну единственную линию квадрата - его нижнюю сторону. Соответственно, мощность множества точек линии окажется меньше мощности точек квадрата в счетное число раз, то есть, в бесконечное. Мощность множества точек квадрата имеет более высокий порядок. Просто результат зависит от способа подсчета и может быть на любой вкус. Два способа мы уже увидели. Рассмотрим еще один.

Рассмотрим эти два объекта в единой метрической системе единиц, в которой размер точки квадрата равен размеру точки линии. Это естественное разумное предложение: бессмысленно приравнивать, скажем, два куска золота, размеры которых неизвестны. Длина стороны квадрата равна a, следовательно, метрически он содержит a² точек. Отрезок по этой же причине содержит a метрических точек. Другим словами, квадрат и линия метрически тождественны. Тогда линия длиной na будет содержать заведомо больше точек, чем квадрат, если n > a.

Такой же результат можно получить и иначе. Возьмем тот же квадрат и разделим его на 4 части. Нижний ряд, два вновь образовавшихся квадрата назовём условно линией. Пока эти два квадрата, понятно, на линию не похожи.

Теперь разделим эти 4 квадрата ещё на 4 части каждый. Нижний ряд из 4 квадратов по-прежнему будем считать линией. Затем вновь каждый квадрат разделим крестом на 4 части. Теперь уже нижний ряд из 8 мелких квадратов отдаленно напоминает некую линию. Посчитаем, отношение количества этих квадратиков в исходном квадрате к их количеству на прообразе линии. По пройденным шагам деления эти отношения равны: 2, 4, 8. Легко обнаружить, что эти отношения будут возрастать по мере дальнейшего деления квадратов по уравнению 2ⁿ× 2ⁿ. Каждый из сомножителей означает, соответственно, деление по вертикали и по горизонтали. Продолжим такое же деление до бесконечности: n → ∞.

Очевидно, что все квадратики станут бесконечно малыми, превратятся в точки и исчезнут из видимости. При этом и линия станет тем, чем мы её обычно и представляем - линией с нулевой толщиной. Что важно, в этом случае и квадрат и линия состоят из одинаковых точек. И количества этих точек будут для квадрата - 2ⁿ× 2ⁿ для линии- 2ⁿ. Отношение количеств или мощностей точек квадрата к точкам линии будет равно 2ⁿ. При увеличении числа шагов деления до бесконечности отношение также увеличится до бесконечности. Это значит, что мощность множества точек квадрата имеет более высокий порядок, чем мощность множества точек отрезка. Конечно, этот способ относится более к алгебре, чем к геометрии, но поэтому в нём и подмены с отождествлением скрыть труднее.

Наконец, можно рассмотреть и классический способ подсчета. Для этого возьмем одну из горизонтальных линий квадрата и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Поскольку координаты точек на отождествляемой линии совпадают с одноименными координатами линии квадрата, то будет пересчитывать одновременно и их: 1, 2, 3 и так далее. Очевидно, что мы получим два тождественных счетных множества. Вряд ли этому следует удивляться, физически и геометрически две линии тождественны. Следует отметить, что здесь мы пересчитываем не координаты, которые обозначаются действительными числами, необоснованно признанными несчетным множеством.

После завершения счета мы обнаруживаем, что одна единственная линия квадрата и отождествляемая с ним линия имеют равные мощности или количества точек. Но на квадрате таких линий - счетное множество (помним и отвергаем утверждение о несчётности действительных чисел). Следовательно, общее число точек на квадрате в счетное множество раз превышает число точек на любом его отрезке и отождествляемой линии.

Однако все рассмотренные отождествления, зависимые от способа счета, построены таким образом, что подсчет числа точек всегда приводит к результату либо большей, либо равной мощности множества точек квадрата по сравнению с множеством точек отрезка. Но можно подобрать и такое правило счета, что соотношение изменится на обратное: окажется, что число точек в отрезках является более мощным множеством. Для этого возьмем не один, а несколько одинаковых квадратов, просто выбрав в кубе несколько разных сечений, и одну линию с длиной ребра куба. Попробуем отожествить все точки этих квадратов с точками на линии. Вновь воспользуемся методикой нумерации точек, предложенной Кантором. Согласно ей, для того чтобы точки на квадратах можно было различить и из очевидных соображений мы обязаны признать, что квадраты имеют ещё одну координату. То есть, каждая точка квадрата в кубе в этом случае характеризуется тремя координатами:

kantor

Для простоты, что, вообще-то, усложняет наше опровержение, ослабляет его, возьмём значения этих координат в кратчайшем виде, в виде единственной цифры от 0 до 9 без последующих дополнительных нулей, что во много раз увеличит число таких комбинированных точек, принадлежащих каждому квадрату. Для определенности возьмем в кубе 10 сечений, причем имеющие точное значение координаты s = 0; 0,1; 0,2 ... 0,9. Теперь создадим по методу Кантора новые числа для точек каждого квадрата. Согласно этому методу каждая точка квадрата будет описываться новым числом - индексом. Исходные координаты задаём в следующем формате:

kantor

из которых формируем индекс:

Здесь символом ? обозначен номер квадрата или, что то же самое, его координата в исходном кубе. Например, точки квадрата с номером s = 0,5 будут описываться индексом:

Как видим, закономерно и оправданно все точки и, соответственно, скомбинированные числа отличаются друг от друга, а все точки этого квадрата расположатся на интервале 0,5...0,6 отождествляемой линии и, более того, на линии останется бесконечное число точек, которым не будет соответствовать ни одна точка этого квадрата. Это точки, для которых индекс должен был бы содержать вместо нулей в позициях, кратных трём, другие цифры. Ничего не изменится, если цифру координаты s ставить в тройках последней.

Такая же ситуация будет наблюдаться с индексами и других девяти квадратов. Легко обнаружить, что комбинированные числа каждого квадрата изменяются в диапазонах, соответственно, [0, 0.1), [0.1, 0.2), [0.2, 0.3) и так далее. Таким образом, мы разместили все точки десяти квадратов на одной линии [0, 1]. Получается, что мощность множества, количество точек квадрата имеет меньший порядок, чем мощность множества точек любой линии. В нашем случае - в десять раз. Но мы могли использовать и другое количество квадратов. Тогда и их точки оказались бы во взаимном однозначном соответствии с точками части отрезка. В этом случае соотношение мощностей станет еще больше и даже, по желанию, в любое число раз.

Очевидно, что такой принцип "сколько будет? а сколько надо?", к которому, по сути, сводится метод Кантора, не может служить основой для корректного математического приема. Но в чем же состоит хитрость, изюминка, так сказать, канторовского метода отождествления? По какой загадочной причине происходит такое противоестественное отождествление? В чем его тайный механизм? Ведь мы же четко видим, что каждой точке квадрата можно однозначно привязать каждую точку линии, причем ни одна из точек не останется без своей единственной пары. А тайна, в сущности, предельно проста. Покажем это на еще одном несколько отвлеченном, но подобном примере.

Возьмем для лучшей визуализации квадрат с бесконечным числом точек в количестве... 1000х1000. Конечно, это на самом деле не бесконечность, но число все-таки очень большое - миллион точек, пересчитать которые вручную будет весьма непросто.

Выберем на этом квадрате одну линию, нижнюю грань квадрата. Согласно методу Кантора присвоим какой-то точке квадрата индекс:

Здесь индекс z сначала представлен с разделительными точками, чтобы было видно, как он образован. Итак, мы получили число z, которое, видимо, точно имеется на отрезке [0, 999]. Правда, настораживает число нулей в этом индексе. Поэтому возьмем для уточнения другую точку на квадрате:

Что-то у нас, как видим, пошло не так. Сразу же можно сделать вывод: на линии [0, 999] такой точки точно нет. В чем же дело? Мы в точности следовали методу Кантора, просто используя отрезок не [0, 1], а более длинный [0, 999]. Принцип тот же, а размеры фигур явно не должны влиять на результат. Иначе получается противоречие: квадрат и линия размером [0, 1] тождественны по мощности, а квадрат и линия [0, 999] имеют уже разные мощности.

Однако именно в этом и состоит хитрость, а по сути подмена понятий в методе Кантора. В нашем случае мы можем попытаться решить проблему такой же дополнительной хитростью. Просто добавим в нашем индексе... запятую. В этом случае подозрительно большое количество нулей сразу превращается в нужное количество:

Вот теперь-то каждая из этих точек уже обязана найти своё соответствие на линии. Но возникает другое противоречие. Координаты всех точек квадрата и линии - целые натуральные числа. А здесь мы получили числа дробные, поэтому отождествлять эти индексы с точками линии мы не имеем права. Зато мы обнаруживаем ту самую загадку метода Кантора для отрезка [1, 0]. Фактически индекс формируется методом, схожим с умножением двух чисел. В нашем случае это соответствие должно выглядеть примерно так:

и для второго примера:

Для сравнения приведем и третий пример:

Как видим, оба метода - умножение и перетасовка цифр - дают числа одного и того же порядка с разрядностью площади квадрата (миллион). При этом можно догадаться, что количество разных произведений координат ровно в два раза меньше, чем количество пар сомножителей, поскольку они могут меняться местами. Действительно, пар сомножителей ровно миллион, следовательно, и произведений тоже ровно миллион. Поскольку существуют симметричные пары сомножителей, то их произведения равны. Следовательно, число уникальных произведений равно полумиллиону. Мы полагаем, что произведение разных чисел дают разные результаты.

При перетасовках цифр смешиваемых пар также ровно миллион, следовательно, и результирующих чисел с перетасованными цифрами также будет миллион. Но в этом случае, что довольно странно, среди них не будет одинаковых. Иначе говоря, при умножении пар какие-то значения в ряду из миллиона чисел будут отсутствовать. Это легко обнаружить: при перетасовке пар может быть получено число 999 999, но при умножении пар такое число получено быть не может - максимальное значение произведения равно 998 001. И таких "отсутствующих" произведений пар - ровно полмиллиона.

Несомненная выгода метода Кантора в том, что каждая точка получит свой индивидуальный, уникальный индекс. Однако остаётся проблема: таких индексов заведомо больше, чем элементов в строке, следовательно, и в отождествляемой линии. Искусственно введенная запятая сжимает эти числа до интервала отрезка [0, 999], но множество из них сразу же становятся дробными, то есть, объективно также не могут этому отрезку принадлежать. Увеличение до бесконечности дискретности квадрата и линии сохранит эту тенденцию без отождествления точек квадрата и линии.

А что же с исходным методом Кантора для единичного отрезка? Там, как видим, произведена точно такая же замена умножения двух чисел на перетасовку их цифр, позволившая получить нужное количество индексов. Порядок чисел при умножении и перетасовке по-прежнему один и тот же. Однако индексы или произведения координат имеют больший порядок дискретности, чем каждая из координат, в том числе, и точки отождествляемой линии. И здесь происходит всё та же подмена понятий при подсчете числа элементов в ряду, что и при подсчете числа четных чисел в натуральном ряду. Только здесь каждой точке линии соответствует бесконечное число индексов точек квадрата. И вот почему.

Понятно, что в числах с бесконечным числом знаков разглядеть это весьма непросто, тем более что все они выглядят одинаково, поскольку одинаково начинаются - с нуля и запятой после него. Сравнивая числа - координату линии (q) и координатный индекс z(x, y), например, для q=x=y=0,1 (точное значение), мы находим z=0,11. Дискретность z в этом случае в 10 раз выше, чем дискретность q. То есть, между двумя дискретными значениями q=0,1...0,2 поместится десять подобных индексов. Если q=x=y=0,12345, то z=0,1122334455 и дискретность z уже в 100000 раз больше дискретности q. Следовательно, между точками q=0,11223...0,11224 (это точные значения) поместится 100000 индексов с дискретностью z. Другими словами, беря две координаты с некоторой дискретностью (числом знаков после запятой), мы получаем индекс с удвоенной дискретностью и степенным увеличением их количества. Сравнивая координаты линии и индексы, мы сравниваем фактически не их значения, которые предельно скрыты от нас и не могут быть равны, а их порядковые номера, которые для счетных множеств, разумеется, всегда найдут соответствие.

Описать этот процесс однозначно и максимально развернуто крайне сложно. Поэтому рассмотрим ещё один пример. Пусть отрезок [0, 1] состоит из миллиарда (10⁹) точек, а соответствующий ему квадрат, следовательно, содержит 10¹⁸ точек. Эти числа являются так же и количествами их порядковых номеров, эквивалентами мощностей этих множеств. Сразу же обнаруживаем, что на линии точек меньше, чем в квадрате. Если постоянно удваивать количество точек вплоть до бесконечности, это отношение будет только возрастать.

Если для отождествления мы возьмём произвольную точку указанного квадрата, то её координатный индекс будет содержать 10¹⁸ знаков после запятой. И мы не имеем никакого права отождествлять этот индекс с точкой на линии, поскольку на ней допустимы только числа с 10⁹ знаков после запятой, точек с такой дискретностью на линии просто нет. При увеличении дискретности квадрата и линии это расхождение будет расти по квадратичному закону.

Кстати, здесь мы наглядно обнаруживаем абсурдность сравнивания количества чисел натурального ряда и его части. Мы можем диагональным процессом Кантора тривиально перенумеровать точки линии и точки квадрата, даже не формируя для них индексы, и получим при этом равенство их количества. Однако мы только что увидели, что такое равенство противоречиво, а попросту его нет. Следовательно, и сравнивание количества членов множеств путем их раздельного пересчитывания - это опасный, ошибочный, некорректный метод, позволяющий получить любой желаемый результат, и которым следует пользоваться предельно продуманно.

Действительно, мы можем сравнивать точки линии и точки квадрата таким же простым раздельным пересчетом, получив в обоих случаях бесконечность. Но это разные бесконечности, бесконечности разной мощности. Напротив, возьмем какую-либо y-линию на квадрате и начнем пересчитывать на ней точки: 1, 2, 3 и так далее. Одновременно с этими точками будем пересчитывать и точки на линии: 1, 2, 3 и так далее. Мы тем самым однозначно отождествим все точки линии со всеми точками на одной из линий квадрата. Остальные линии квадрата, с другими координатами, разумеется, останутся без номеров. Это самый правильный способ пересчета и отождествления.

Итак, даже при ослаблении нашей аргументации мы приходим к выводу, который противоречит выводу Кантора об их равенстве. Два способа нумерации, основанных тождественно на одном и том же методе, приводят к несовместимым, противоположным выводам. Поэтому этот метод Кантора логически неверен, ошибочен. И вновь возникает риторический вопрос, какой же в этом случае метод верный? Методов группировки может быть сколько угодно, поэтому верным является только один метод - без группировки, то есть, сравнивать можно только равнозначные объекты - линию с линией. В этом случае вывод однозначный - множества точек линии и квадрата не равномощны. Самым простым и наглядным способом определения этого является простое наложение линии на квадрат и отождествление соприкоснувшихся точек.

Практически такая же противоречивая ситуация возникает и при отождествлении двух противоположных сторон квадрата: верхней и нижней, либо любых двух средних линий квадрата. Возникает совершенно противоестественная ситуации: эти пары линий вообще нельзя отождествить, поскольку нумерация их точек не имеет одинаковых значений. Верхняя сторона квадрата должна иметь по Кантору значения первой цифры после запятой всех точек, начинающиеся с 9, а нижняя - с 0, а средние, например, с 3 и 5. Две явно одинаковые линии оказываются несопоставимыми.

Стереографическая проекция

В заключение отметим, что один из истоков или примеров отождествления бесконечностей разной мощности можно обнаружить в механизме стереографической проекции, также фактически отождествляющей точку и отрезок. Рассмотрим соотношение между размерами двух отрезков, которые затем сожмем в точки:

kantor

Рис.3. Стереографическая проекция отождествляет отрезок и точку

Мы не описываем сущность стереографической проекции, её описание можно найти в литературе. Каждая проекционная линия, прямая делится проецируемой точкой окружности между полюсом и проекционной плоскостью на две части, например, l₁ и l₂. Возьмем частный случай, когда отрезок делится пополам, то есть, l₁ = l₂ = l. Проведем ещё одну проекционную линию под углом ? к исходной линии. В этом случае на окружности образуется дуга, а на плоскости - отрезок. Проведем из проецируемой точки пересечения дополнительный отрезок между проекционными лучами параллельно плоскости из проецируемой точки. Обозначим полученный отрезок через b, а проекцию на плоскости - через a. Из подобия треугольников следует, что

kantor

Здесь знак неточного равенства взят из предположения, что отрезок b приблизительно равен длине дуги. Это не точное равенство, но в средней части окружности отрезок и дуга отличаются друг от друга незначительно, в конечное число раз. Теперь найдем предел этого отношения, когда угол между двумя проецирующими прямыми стремится к нулю:

kantor
(9)

Это очевидный и аналитически достоверный предел. Но при этом возникает вопрос: что же означает это отношение 2? Две проекционные прямые слились в одну, и эта прямая пересекает и окружность и плоскость в одной точке каждую. Что же означает это соотношение для двух разных точек? Если считать, что точка - это то, что не имеет частей, то ответ становится совершенно туманным. Выходит, что точки не имеют частей, но в разном количестве. В любом случае для утверждения, что точка на окружности спроектировалась в единственную тождественную точку на плоскости, четких, бесспорных оснований уже нет.

Однако это соотношение мы нашли для конкретного, среднего угла. А что если пару прямых, проектирующих лучей повернуть ближе к горизонтальному направлению? То есть, устремить к нулю не только угол между проецирующими прямыми, но и их средний угол к плоскости. В этом случае мы увидим, что отношение будет стремиться к бесконечности:

kantor

Вопрос о смысле этого отношения становится еще более острым. Если две точки - исходная, проецируемая и её проекция - отождествляются, тогда что означает это отношение? Изначально оно составлялось как отношение длины проецируемого отрезка и проекции, которые в дальнейшем уменьшением угла до нуля были преобразованы в точки. Хотя точка и не имеет частей, но величина соотношения определенно выглядит как количество проецируемых точек в проекции. Звучит весьма странно: проецирующий луч создаёт проекцию, имеющую явно не нулевые, не точечные размеры. Можно сколько угодно с этим не соглашаться, но как можно иначе рационально объяснить это соотношение?

Обычно бесконечно малые величины в алгебре характеризуются параметром порядка малости. Если две величины имею отношение конечной величины, то они считаются величинами одного порядка малости. Если отношение стремится к бесконечности, то величины имеют разный порядок малости. С учетом этого следует предположить, что стереографическая проекция окружности на плоскость некорректна, а проекциями её точек фактически являются плоские фигуры, отрезки.

Рассмотрим эту же ситуацию с другой точки зрения, не отождествляя дугу окружности и прямой отрезок. Для этого нам понадобится следующее интересное соотношение, теорема. Если к отрезку дуги провести по два луча из центра окружности (рис.4) и из любой точки окружности, кроме точек этой дуги, то угол между лучами в первом случае будет в два раза больше угла между лучами во втором случае. Приведем краткое доказательство этой теоремы.

kantor

Рис.4. Теорема об углах на дуге окружности

Итак, возьмем на окружности рис.4 некоторую произвольную дугу CB и проведем к ней две пары лучей - из центра и из полюса О. Проведем далее вспомогательный диаметр BD и линию CD. Обозначим одинаковыми буквами равные углы в равносторонних треугольниках у равных сторон. По условиям задачи нам задан некий центральный угол a. Докажем, что а = 2x. Из построений на рисунке видим:

kantor

Угол при вершине штрихового треугольника:

Углы при основании равностороннего треугольника.

kantor

Углы при основании равностороннего треугольника с искомым углом:

Составляем баланс углов в треугольнике с искомым углом x:

Подставляем условно известное значение угла f:

Раскрываем скобки

kantor

Подставляем значение заданного угла а

kantor

Упрощаем выражение

kantor

Что и требовалось доказать.

Согласно этой теореме, на рис.3 длина дуги окружности в пределах угла α равна 2αR, поскольку угловая величина дуги равна 2α. Длину линии проекции a в основании проекционного угла найдем как разницу сторон двух прямоугольных треугольников:

kantor

Отсюда находим величину а:

kantor

Как и выше, найдем отношение длины отсекаемой на окружности дуги к длине этого отрезка:

kantor

Найдем предел этой величины, когда каждый из углов стремится к нулю. В этом случае обе проекционные линии сблизятся до слияния, а их средняя линия будет стремиться к горизонтальному положению:

kantor

В общем случае мы получаем неопределенность, поскольку к нулю стремятся и числитель и знаменатель. Поэтому мы поступим следующим образом. Найдем эти пределы для нескольких конкретных значений среднего проекционного угла φ. В этом случае неопределенность не устраняется, но мы табличным методом построим соответствующие графики, которые визуально продемонстрируют наличие конечных пределов. Табличные значения сходятся удовлетворительно быстро, поэтому в пределах точности приложения Excel были получены следующие значения пределов для произвольно взятых значений угла φ:

Как видим, пределы существуют для любого значения проецирующей линии, угла проецирования. Поскольку вычисление предела функции неочевидно, приведём геометрический способ его вычисления для частного значения угла, рассмотренного на рис.3, значение которого определяется из геометрических соображений и равно 45^о. Увеличим до бесконечности масштаб фрагмента рисунка в точке пересечения проецирующей прямой и окружности:

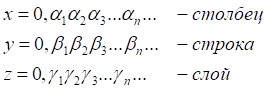kantor

Рис.5. Увеличенный фрагмент рисунка 3

На рисунке угол φ =45^о, а угол α → 0. Как видим на рисунке, фрагмент проецируемой окружности выглядит вертикальной прямой, а две проецирующие прямые - параллельны. Следовательно, отрезки b - на окружности и параллельный проецирующей плоскости оказываются перпендикулярными и образуют равносторонний прямоугольный треугольник. Отсюда и следует значение предела lim = 0,5 в третьей строке таблицы пределов и в выражении (9). Очевидно, что геометрическое вычисление предела несложно сделать и для других углов проецирующего луча. Напротив, определить это значение аналитически, вычислением предела выражения:

kantor
(10)

довольно сложно. Подставим значение угла φ

kantor

Как видим, под знаком предела находится разность двух бесконечно больших величин, причем это не просто равномощные бесконечности, они тождественны. Действительно, в пределе α → 0 мы имеем:

kantor

Что и можно записать как тождество

kantor

Это довольно интересное обстоятельство: две бесконечности равны, однако, тем не менее, дают разность 2. В общем-то, это свойство не уникально. Его легко показать на другом примере: n +2 = n, если n →∞. Здесь также две равные бесконечности, но при вычитании одной из другой мы получаем конечное число. Значение предела (10) нам известно, он равен 2, то есть при α → 0 мы имеем

kantor

Получается, что тангенс в знаменателе, меньший единицы на бесконечно малую величину, вносит в значение бесконечно большой величины весьма существенный вклад, увеличивая её ровно на 2. Прямое вычисление выражения (10) в приложении Excel при уменьшении угла α до величины 10^-9 дало устойчивое стремление значения предела к 2 с погрешностью 10^-8. Дальнейшее уменьшение угла не имеет смысла ввиду ограниченной точности вычисления функций приложением.

Таким образом, можно достаточно уверенно заявить, что стереографическое проецирование, преобразование фактически отождествляет точку и линию. И только единственная - вертикальная - проекция отождествляет точку на сфере с точкой на плоскости - это точка их касания. Верхняя точка, полюс проецируется фактически в линию бесконечной длины.

Здесь мы рассматривали проецирование круга. Очевидно, что точка сферы проецируется не в отрезок, а в плоскую фигуру. В этом случае явно напрашивается предположение о форме самого проецирующего луча, который теперь уже формально может и даже обязан иметь некое сечение: круглое, квадратное, в форме звезды и так далее.

Вместе с тем, вполне ожидаемо может возникнуть возражение: а почему, собственно, мы рассматривали две проецирующие линии? В традиционном варианте линия всегда одна, поэтому, казалось бы, проекцией каждой точки может быть только точка. Сразу же можно заметить, что это весомый довод в пользу формализма Кантора, который весьма схожим способом отождествил множество точек линии с множеством точек плоской фигуры - квадрата.

Ответ достаточно простой. Рассмотренный способ показывает, что любые две смежные бесконечно близкие точки окружности (сферы) на проекционной плоскости позволяют поместить между ними некоторое количество, вплоть до бесконечности, таких же точек. Если рассматривать дискретное пространство, вплоть до планковских размеров, то появление на проекции дополнительных элементов практически неразрешимая проблема. Единичный проекционный луч просто делает эту проблему незаметной.

С другой стороны, стремление к нулю угла между рассмотренными проецирующими лучами отождествляет их, превращает в одну линию, единый луч. И в этом случае возникает важный встречный вопрос: что же тогда означают вычисленные пределы? Какой математический, физический и даже философский смысл имеют эти величины? Ответ очевиден: это скрытное канторовское отождествление точки и линии, того, что не имеет частей, с тем, что может делиться на части.

Литература

Ссылки проверены и исправлены 15.05.21

1. Бесконечность, Википедия, URL: https://ru.wikipedia.org/wiki/Бесконечность

2. Виленкин А., Мир многих миров: Физики в поисках параллельных вселенных Алекс Виленкин, пер. с англ. А. Сергеева. -- М.: ACT: Астрель : CORPUS, 2010. -- 303, [1] с. -- (ЭЛЕМЕНТЫ)

3. Виленкин Н.Я., В поисках бесконечности.-- М.: Наука, 1983. 160 с.

4. Горелик Г.Е., Почему пространство трехмерно? М.: Наука, 1982, 168 с.

5. Крейг У., Самое начало. Происхождение Вселенной и существование Бога, URL: http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml

6. Линде А.Д., Инфляция, квантовая космология и антропный принцип. Перевод Карпова С., URL: https://arxiv.org/abs/hep-th/0211048

7. Новиков И. Д., Черные дыры и Вселенная. -- М.: Мол. гвардия, 1985. -- 190 с., ил.-- (Эврика).

8. Парадокс Гильберта, URL: http://pikabu.ru/story/paradoks_gilberta_1962200 (статья и фильм отсутствуют, осталисть только комментарии)

9. Парадокс Гильберта, URL: http://traditio.wiki/Парадокс_Гильберта (текст статьи изменён)

10. Парадокс Гильберта 'Гранд-отель', Википедия, URL:
https://ru.wikipedia.org/wiki/Парадокс_'Гранд-отель' (текст изменён)

11. Путенихин П.В. Логика противоречий. - Саратов: "АМИРИТ", 2017. - 133 с., илл., URL:
https://www.elibrary.ru/item.asp?id=42733187
https://www.twirpx.org/file/3089642/

12. Ченг Ю. Математический беспредел: от элементарной математики к возвышенным абстракциям / Юджиния Ченг; [перевод с английского А. Шмид]. - Санкт-Петербург [и др.] : Питер, 2019. - 332 с. : ил., табл.; 21 см.; URL: https://www.klex.ru/xuq

Путенихин Петр Васильевич Правила счета элементов бесконечного множества

Путенихин Петр Васильевич
Правила счета элементов бесконечного множества