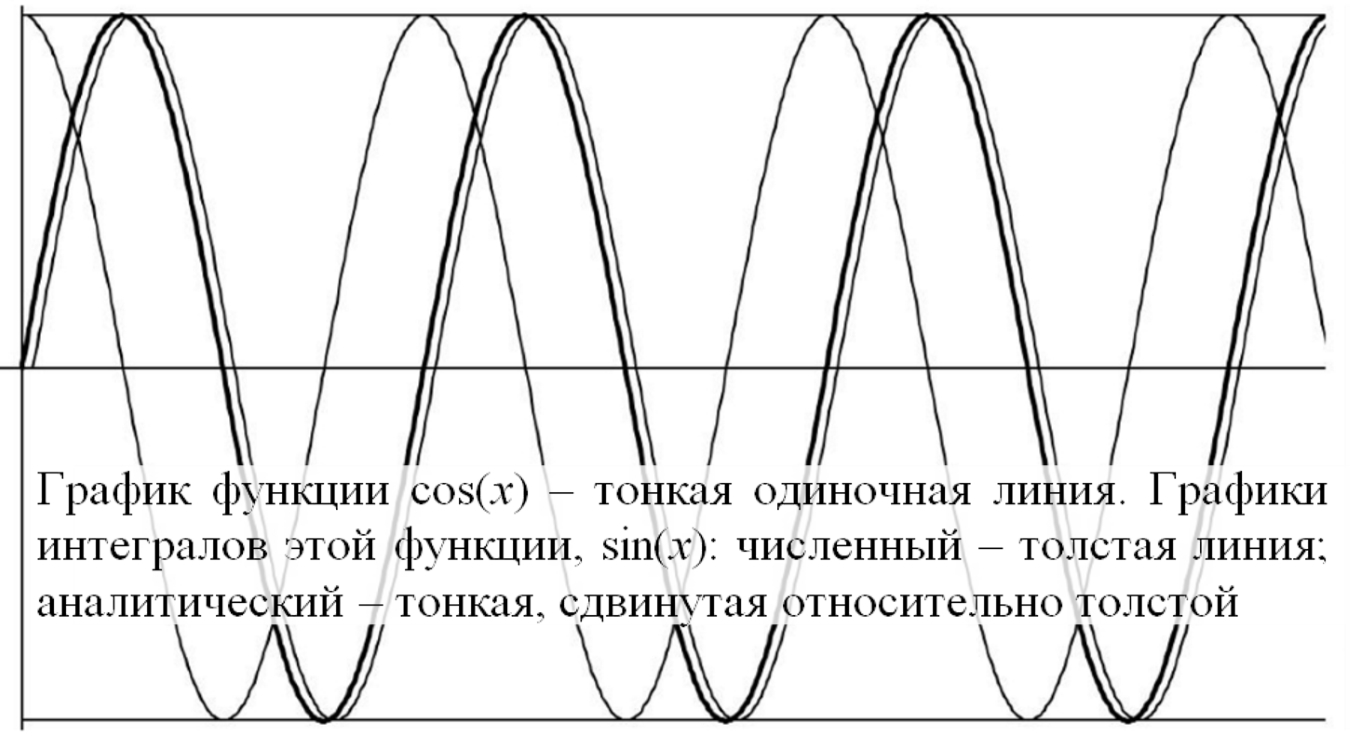
Рис.1.1. Числовой интеграл функции cos(x)

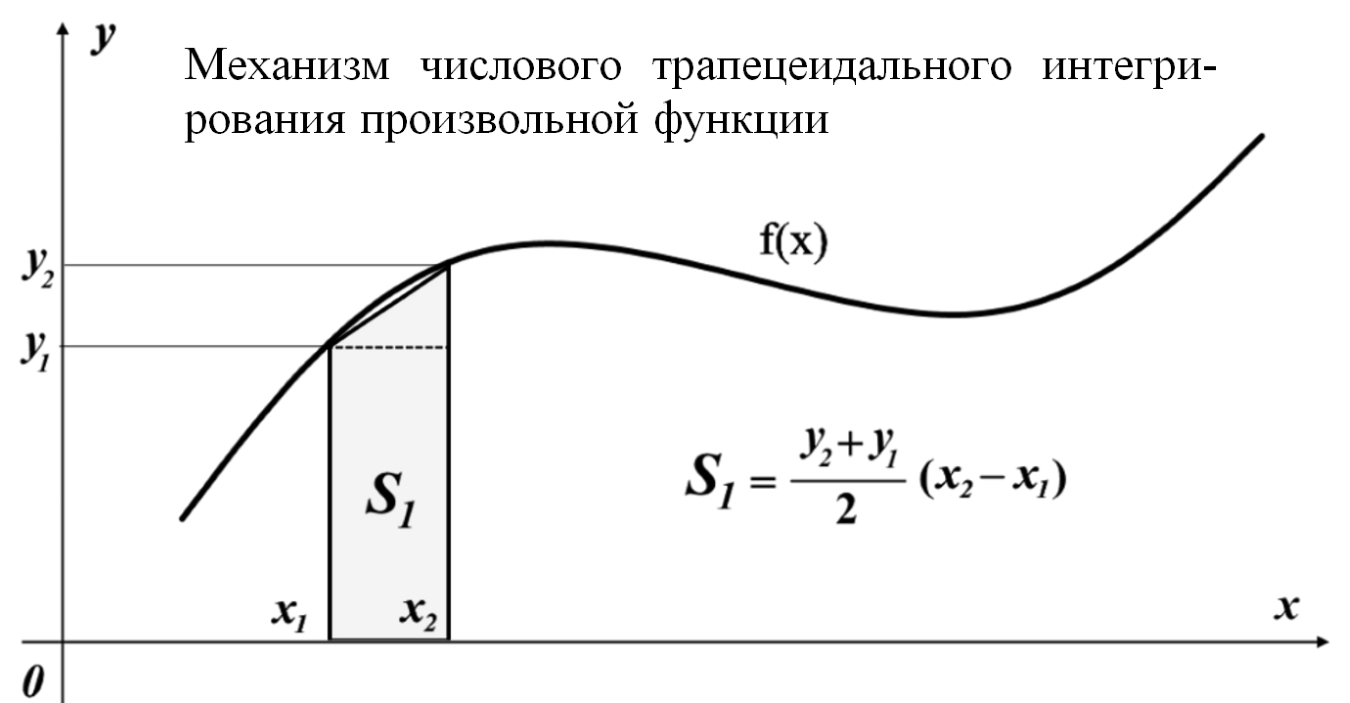
Рис.1.2. Площадь интегральной трапеции

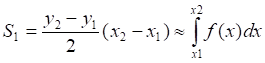
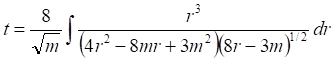
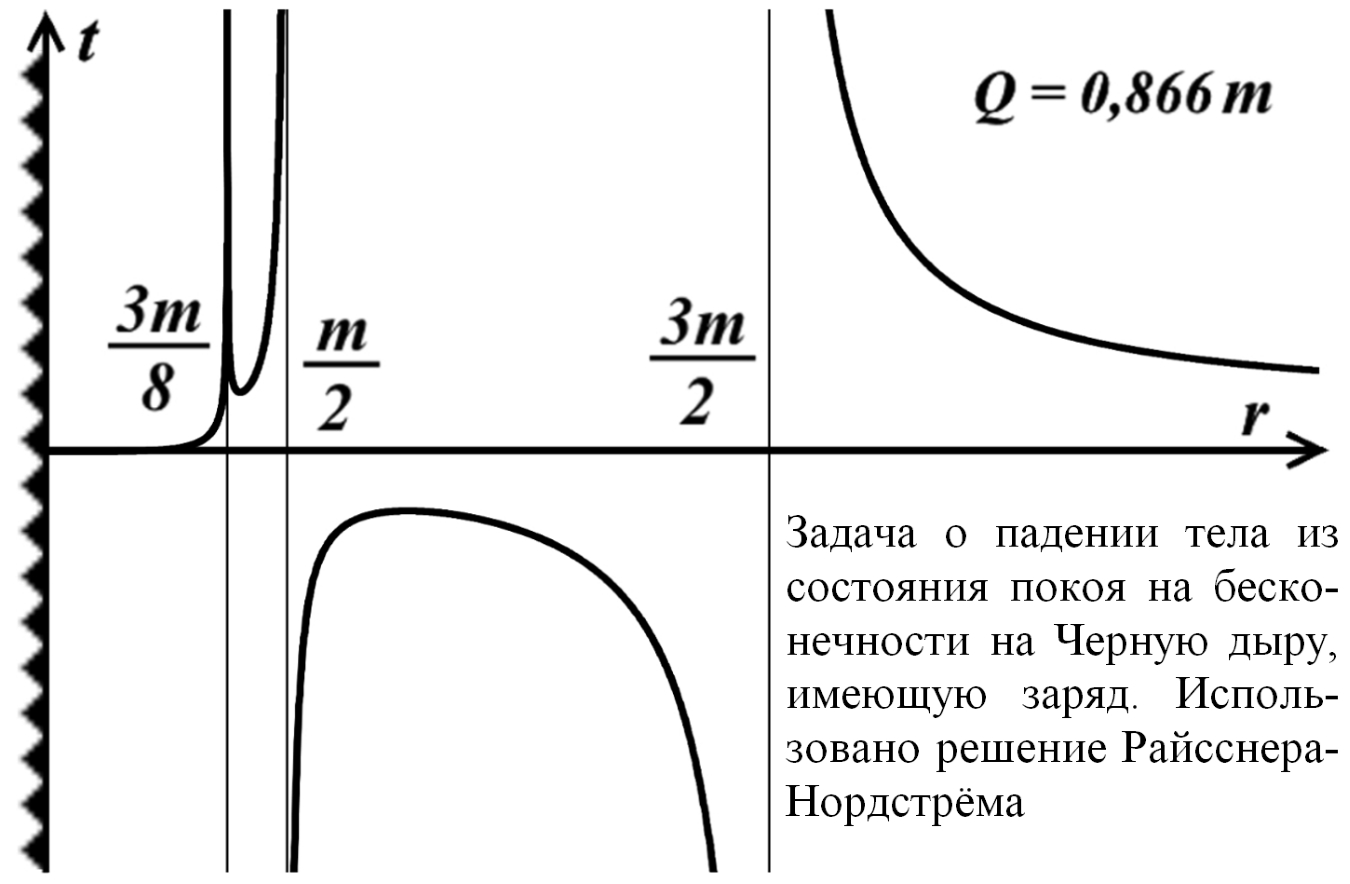
Рис.1.3. График подынтегральной функции [1, с.255, рис.4.32]

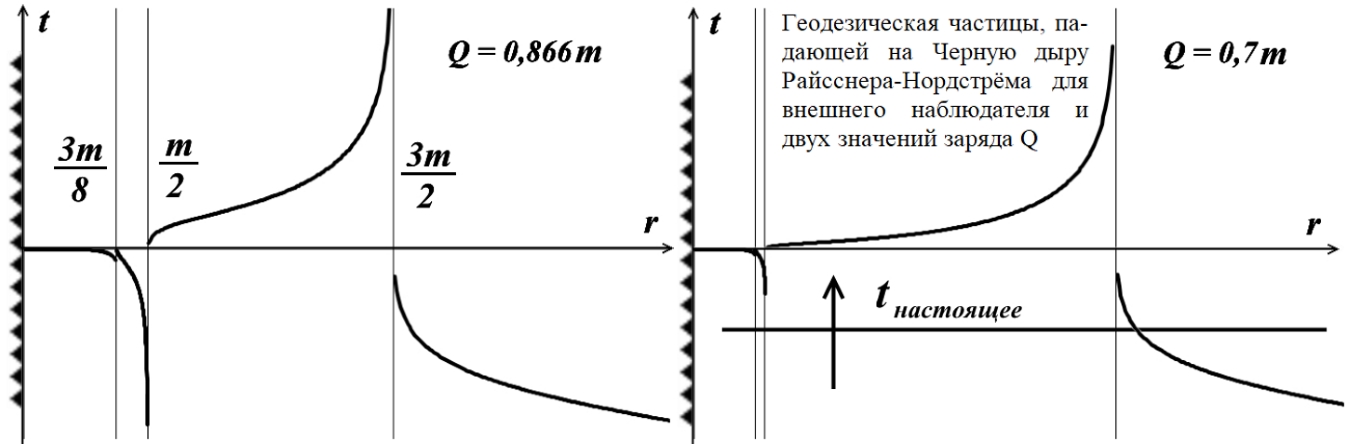
Рис.1.4. Геодезическая частицы, падающей на Чёрную дыру Райсснера-Нордстрёма для внешнего наблюдателя и двух значений заряда Q [1, с.257, рис.4.33]

Рис.1.5. Условный график числа π

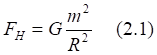
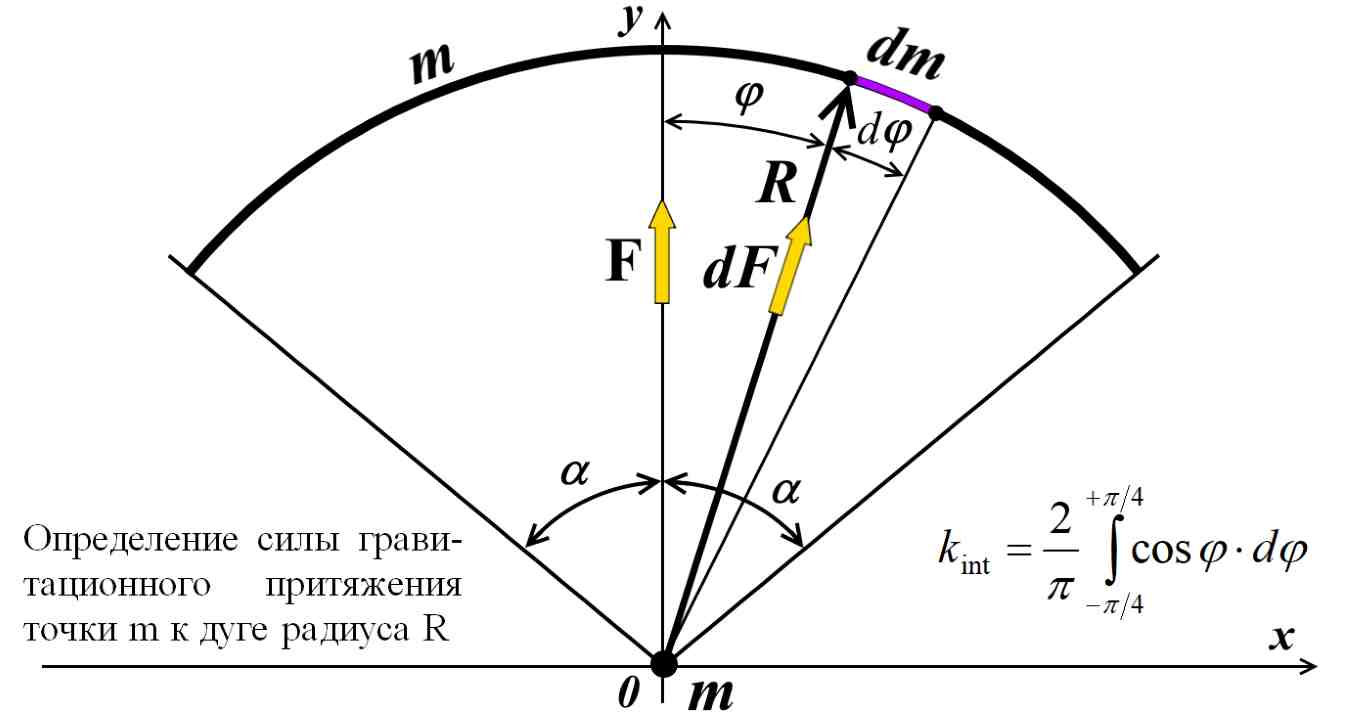
Рис.2.1. Притяжение точки к дуге

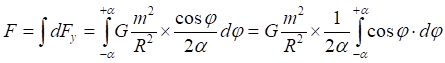
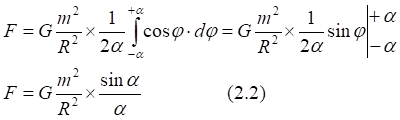
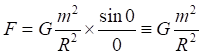
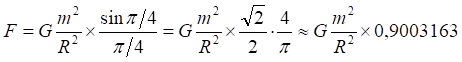
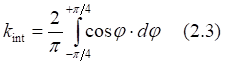
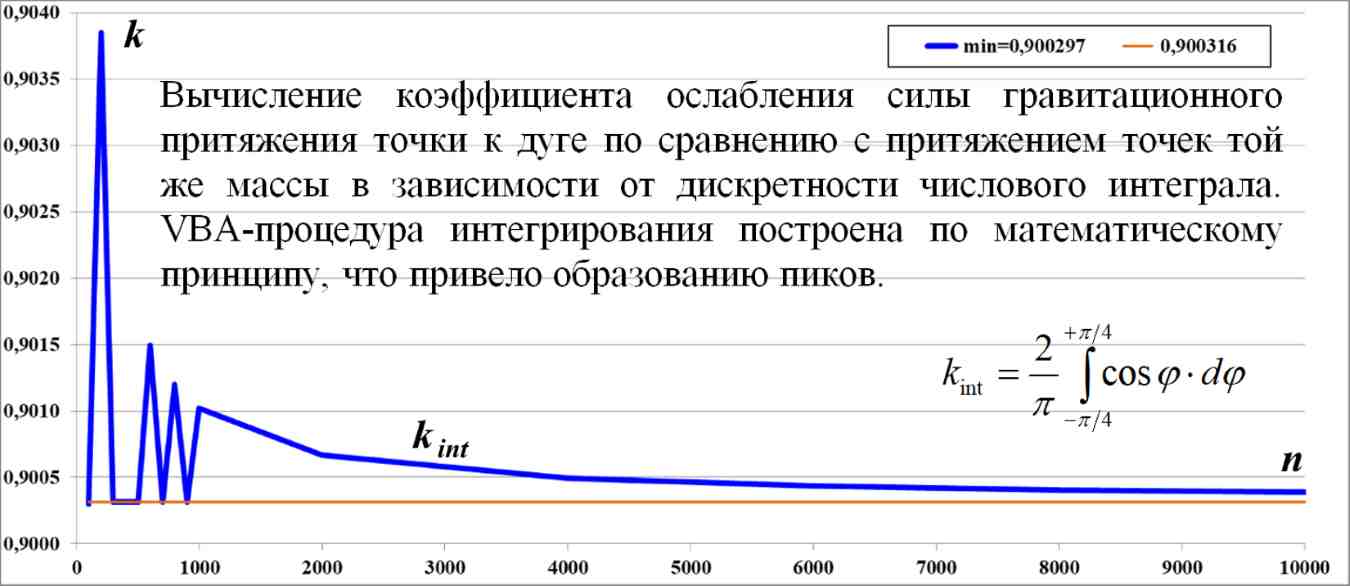
Рис.2.2. Численное интегрирование с разным числом дискрет

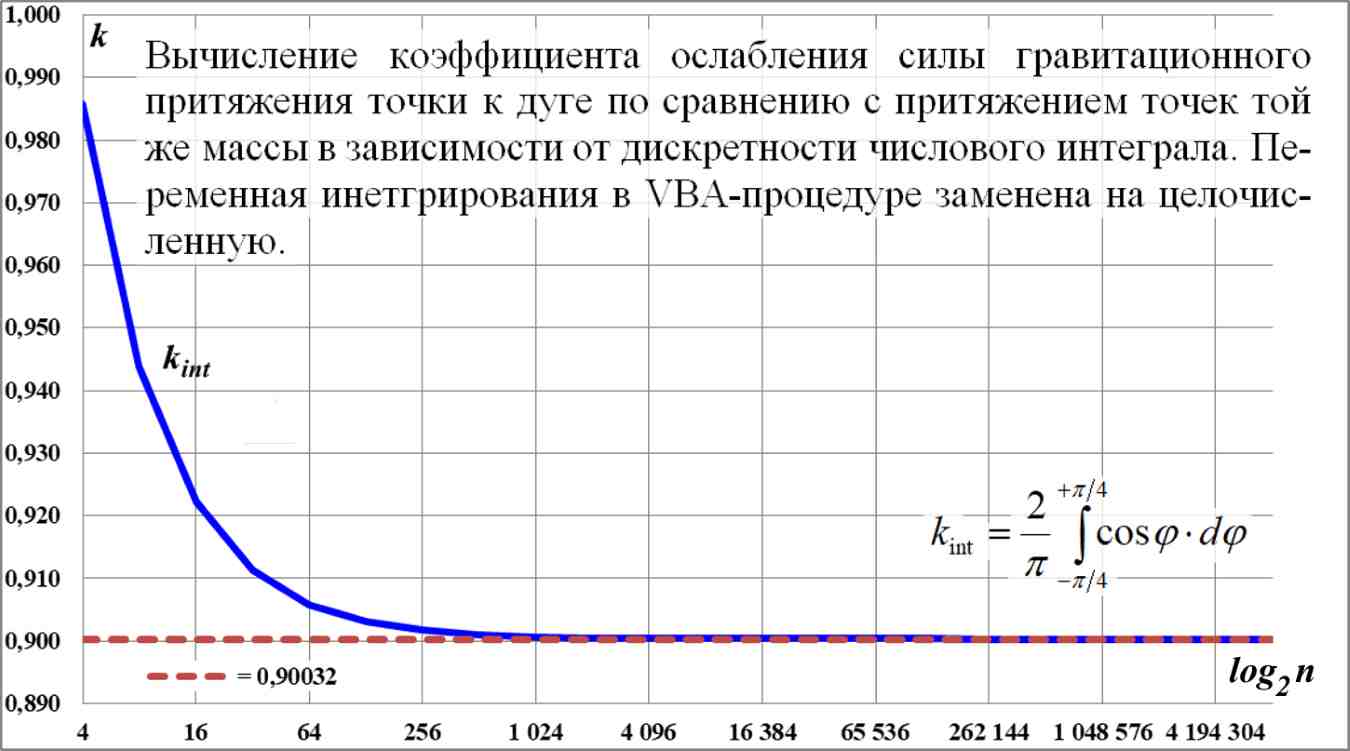
Рис.2.3. Численное интегрирование с разным числом дискрет на предельно большом интервале дискретизации

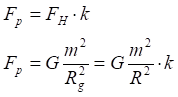
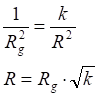
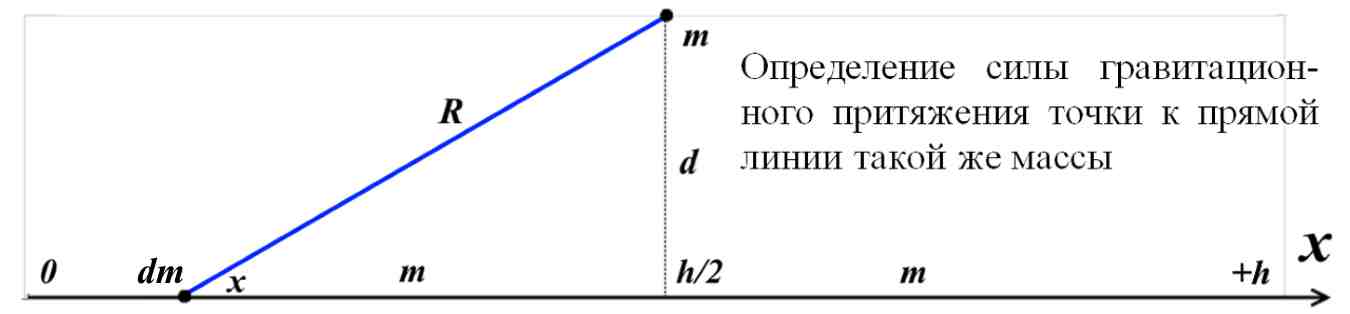
Рис.3.1. Гравитационное притяжение точки к линии

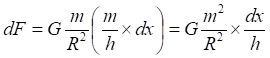
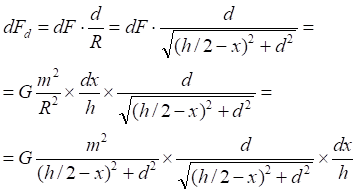
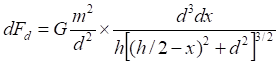
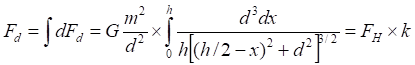
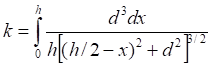
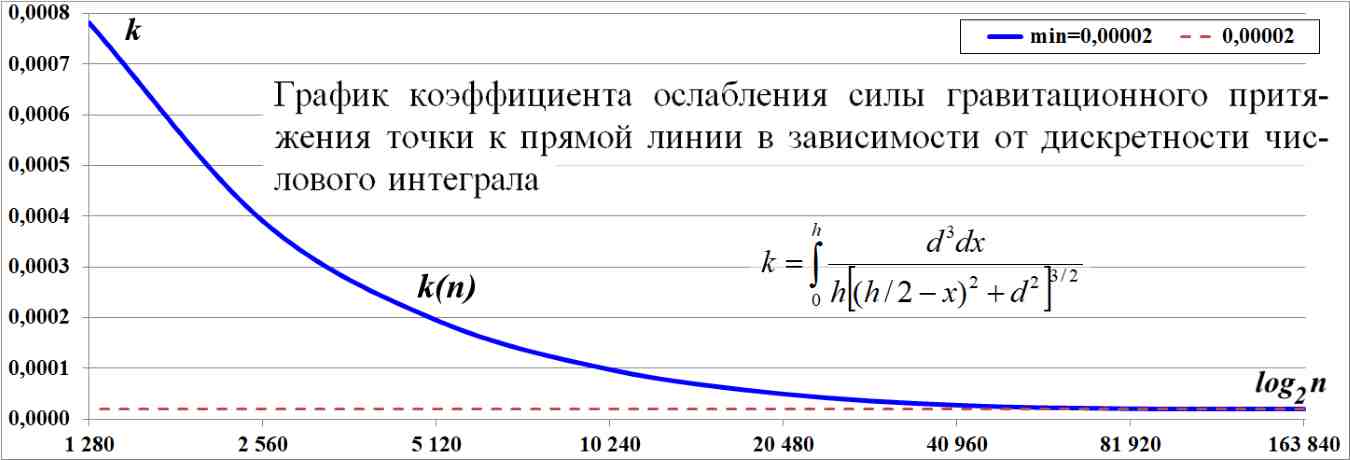
Рис.3.2. Величина коэффициента уменьшения силы притяжения точки к линии в зависимости от дискретности численного интеграла

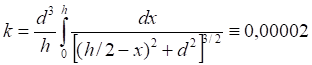
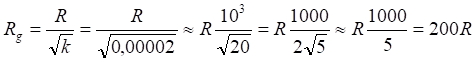
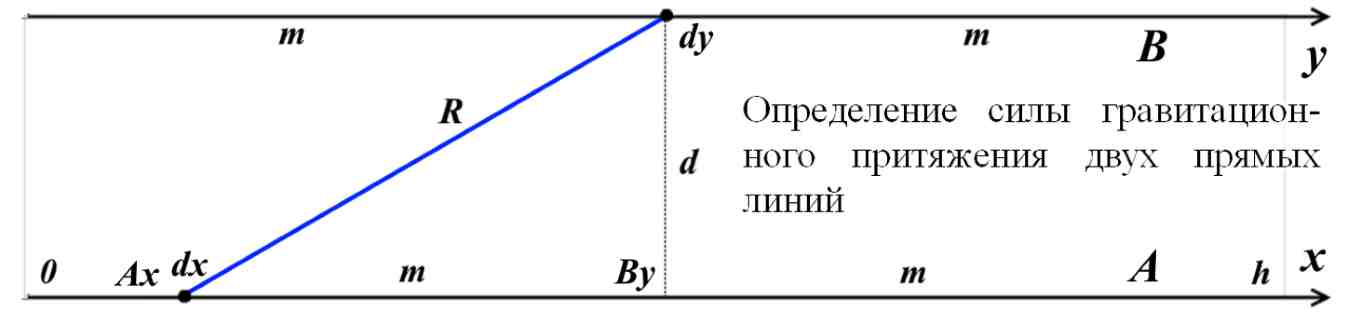
Рис.4.1. Гравитационное притяжение двух линий

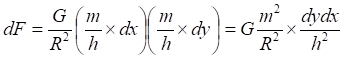
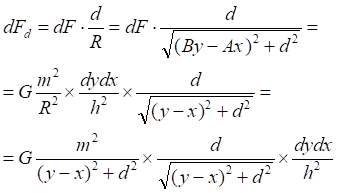
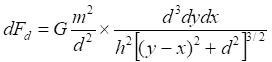
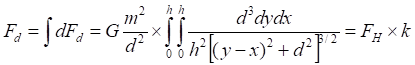
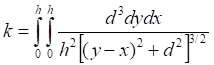
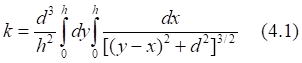
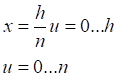
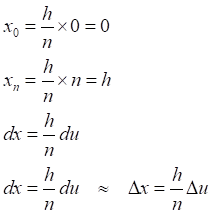
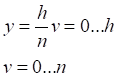
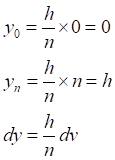
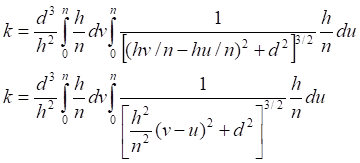
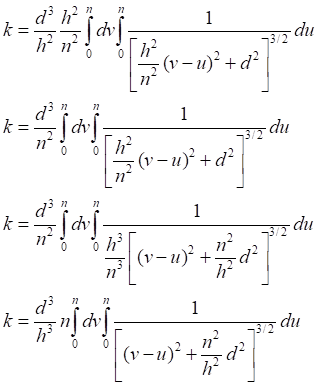
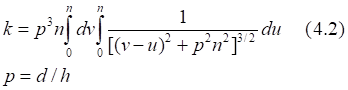
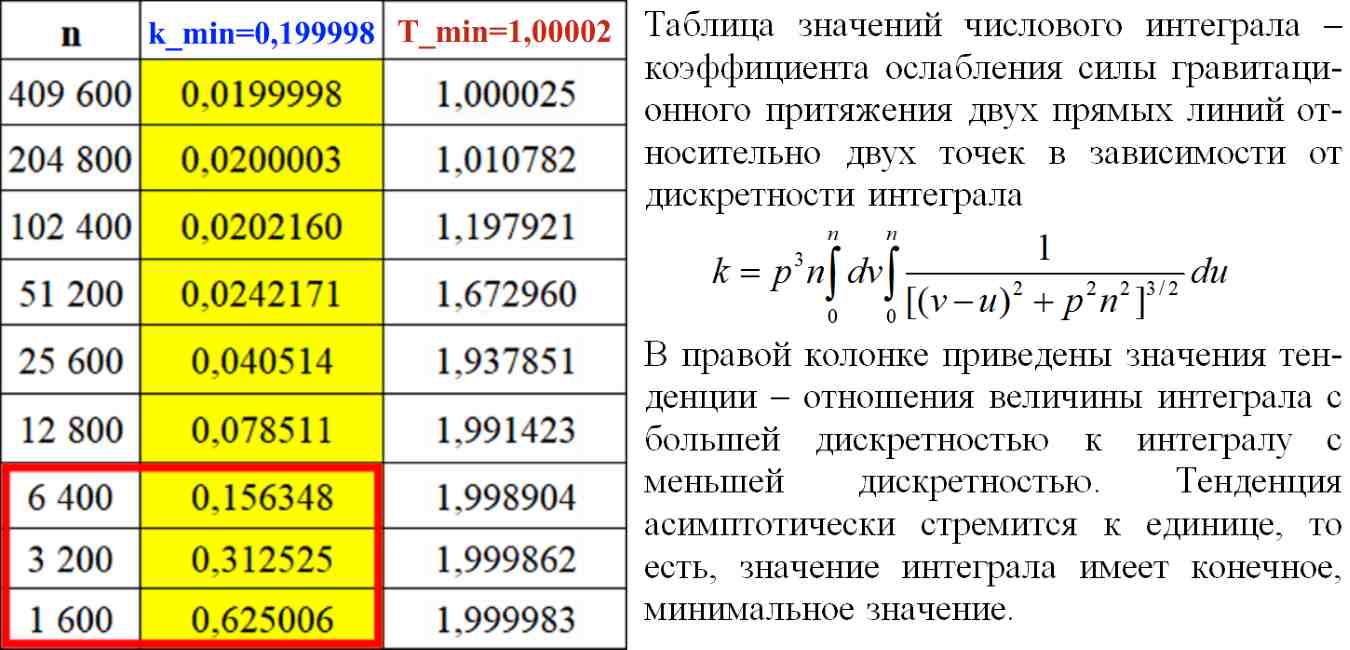
Таб.4.1. Таблица значений числового интеграла (4.2)

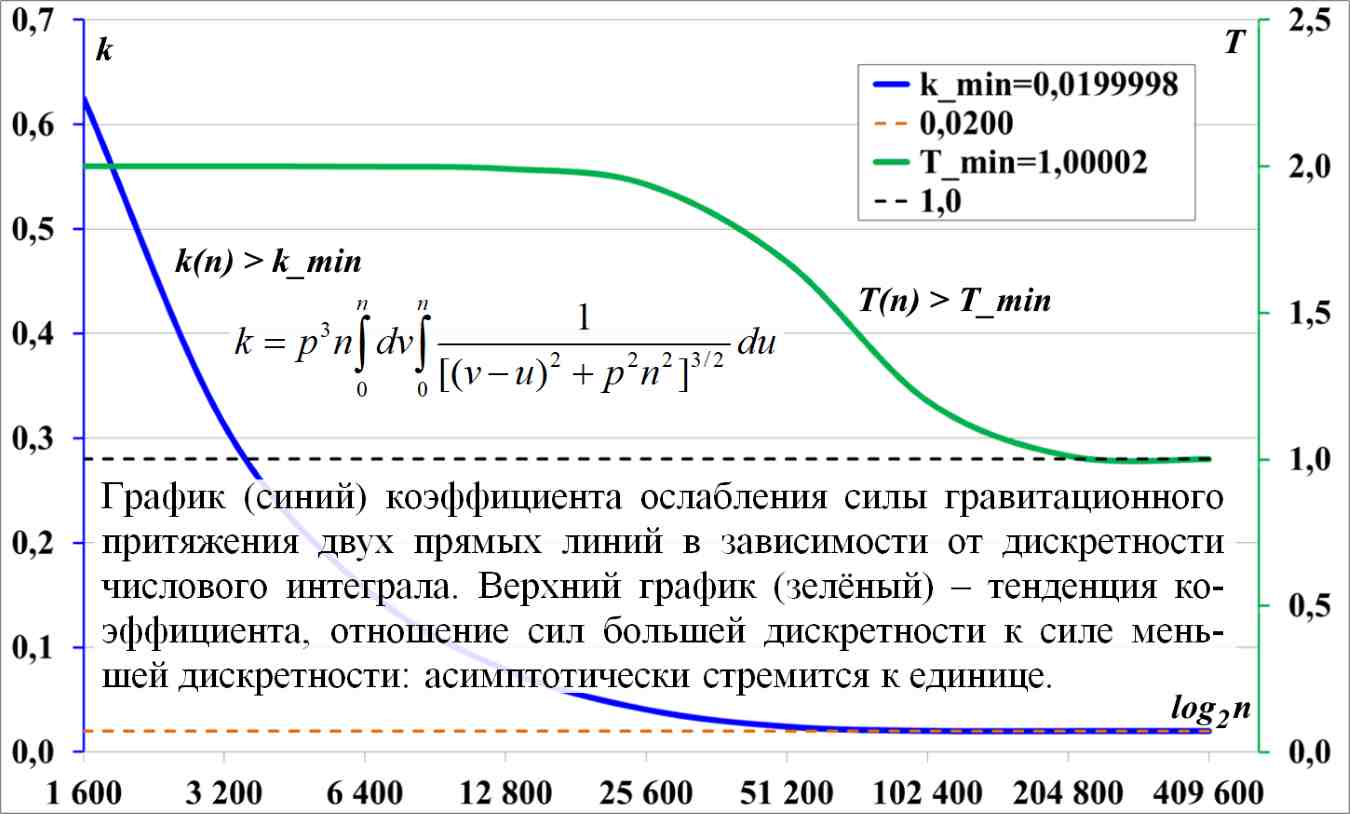
Рис.4.2. График зависимости коэффициента (синий) от дискретности интеграла и график тенденции (зелёный) его уменьшения

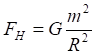
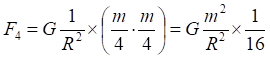
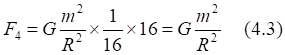
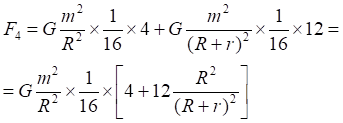
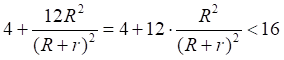
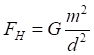
Рис.5.1. Сила гравитационного притяжения элементарных площадок на двух зеркалах

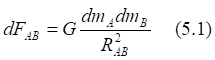
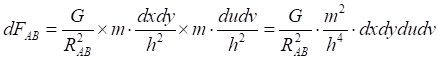
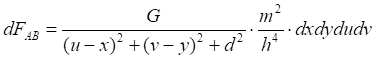
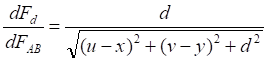
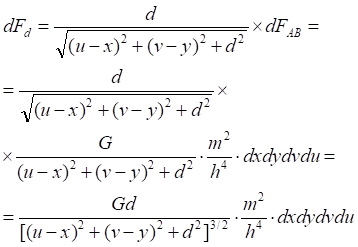
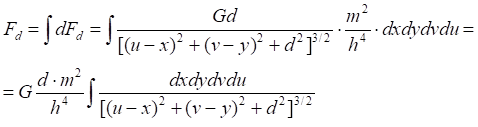
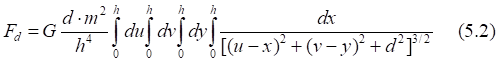
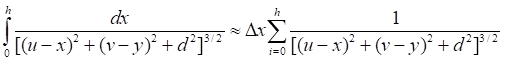
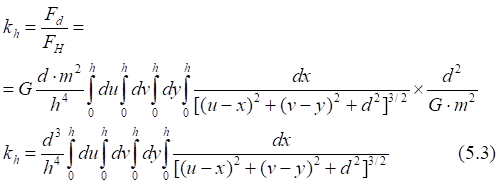
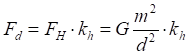
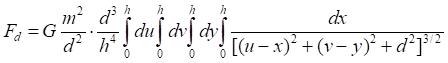
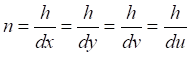
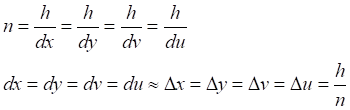
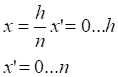
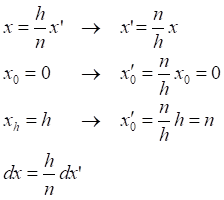
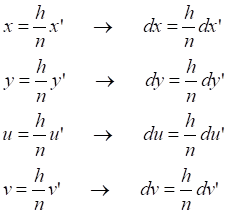
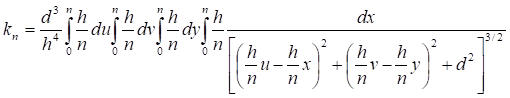
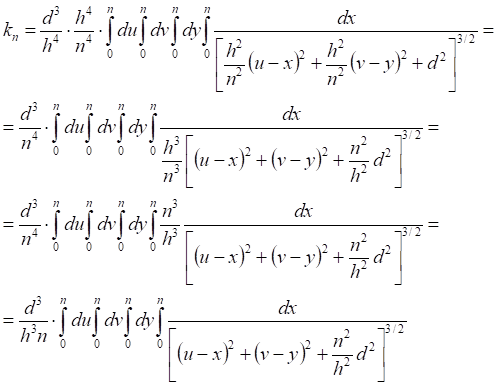
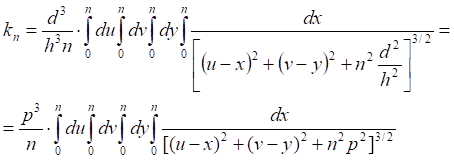
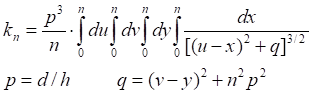
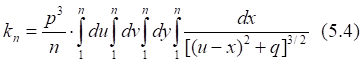
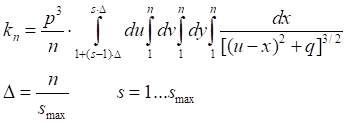
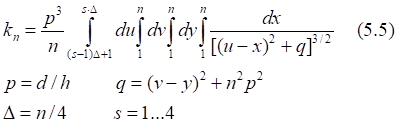
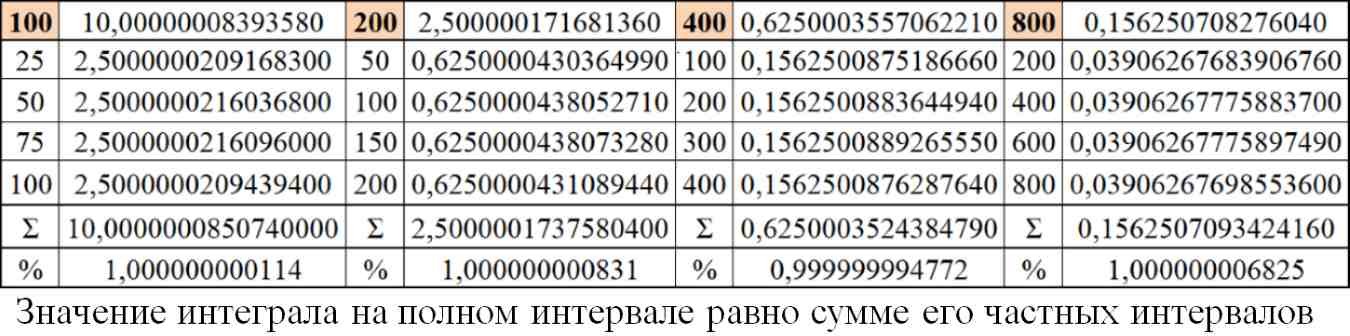
Таб.5.1. Значение интеграла (5.5) на полном интервале равно сумме его частных интервалов

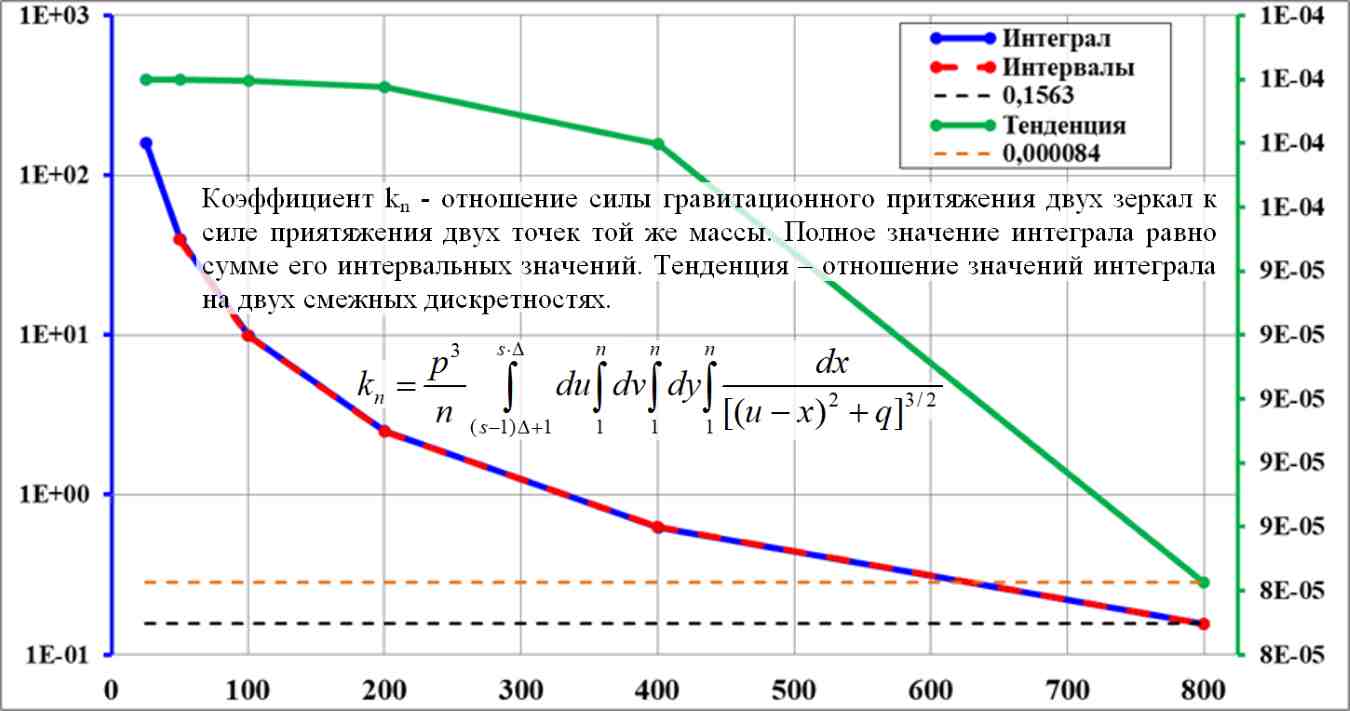
Рис.5.2. Интеграл на полном интервале равен сумме интервальных интегралов

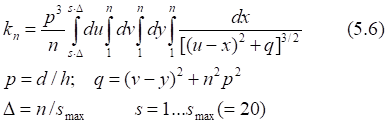
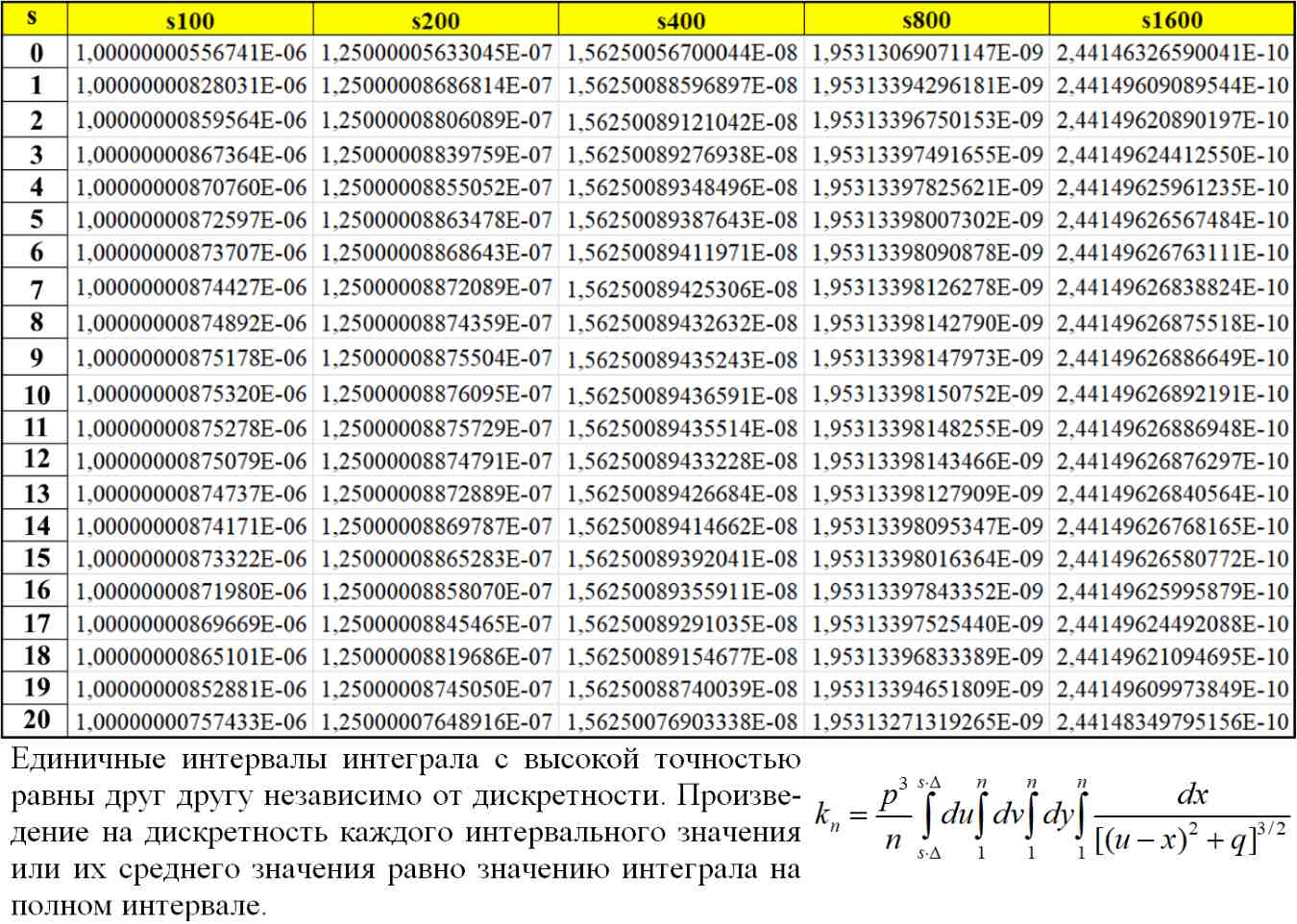
Таб.5.2. Единичные интервалы интеграла (5.6) с высокой точностью равны друг другу

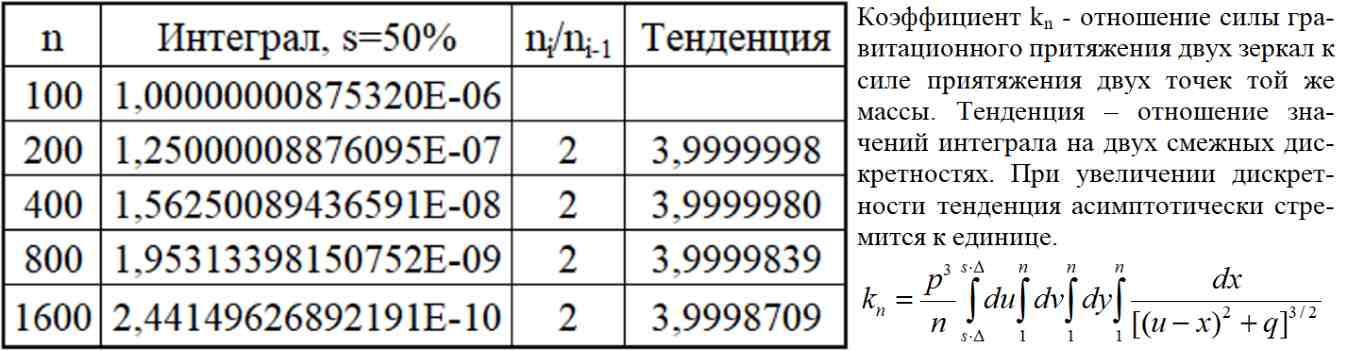
Таб.5.3. При увеличении дискретности отношение двух смежных значений интеграла (5.6) стремится к единице

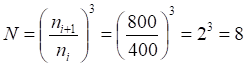
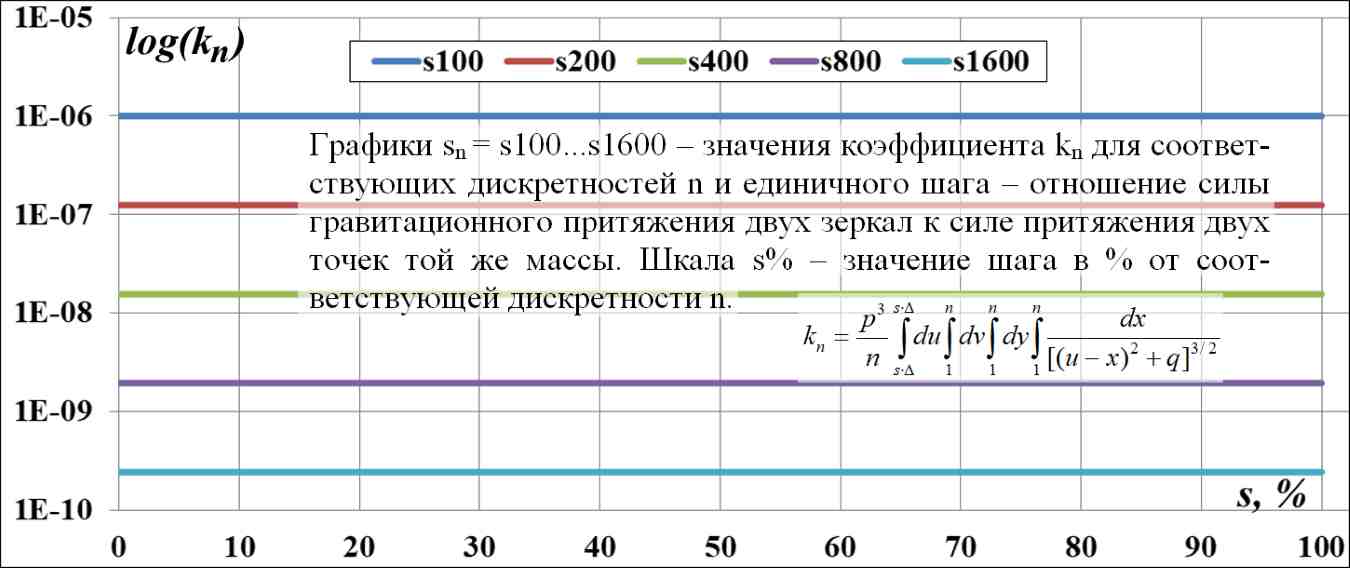
Рис.5.3. Диаграммы k(n) для дискретностей n = 100...1600 и единичных интервалов s% от дискретности. Шкала k(n) логарифмическая

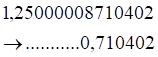
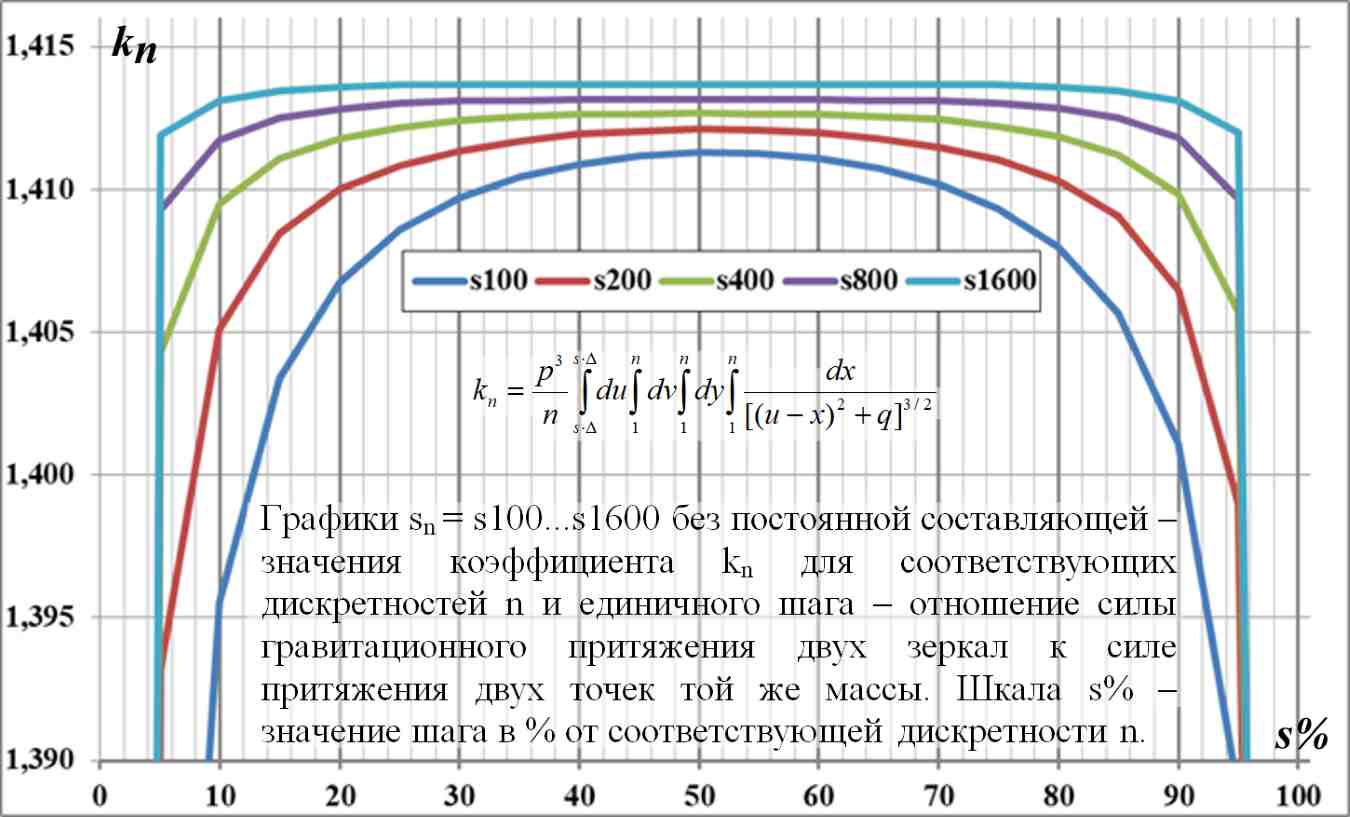
Рис.5.4. Диаграммы k(s%) без постоянной составляющей

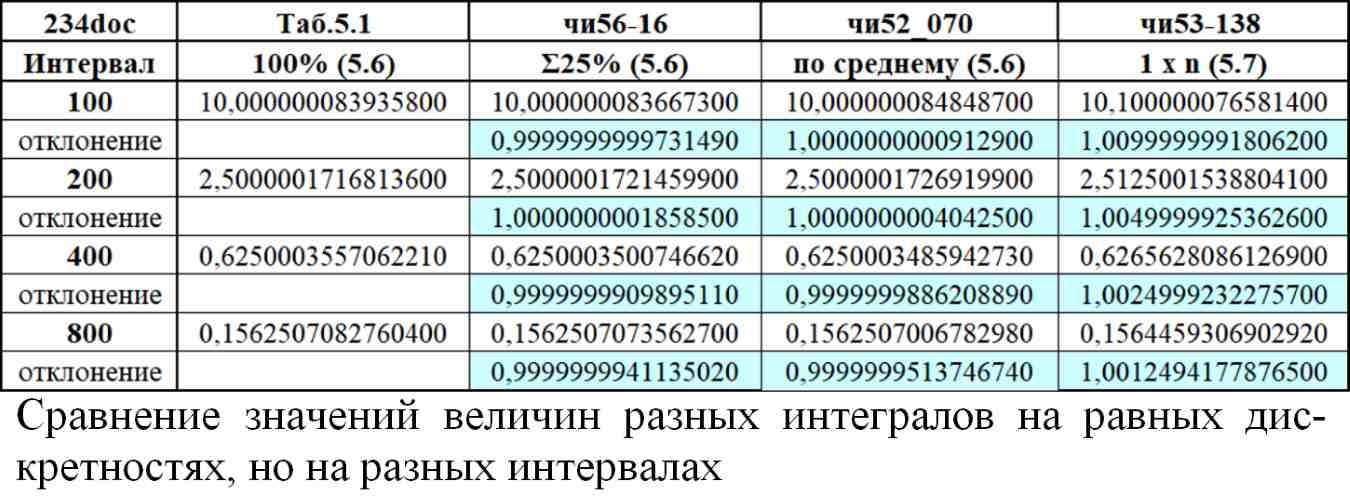
Таб.5.4. Сравнение значений величин разных интегралов

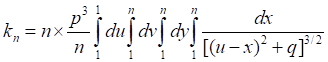
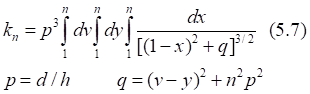
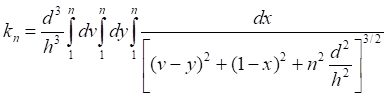
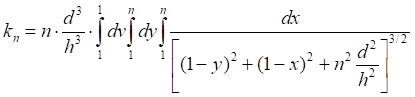
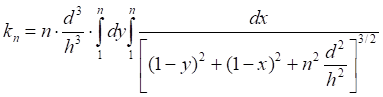
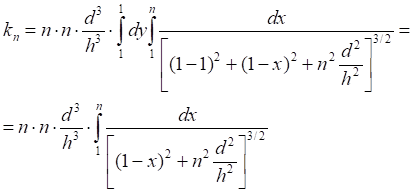
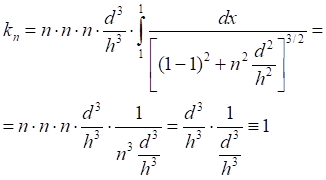
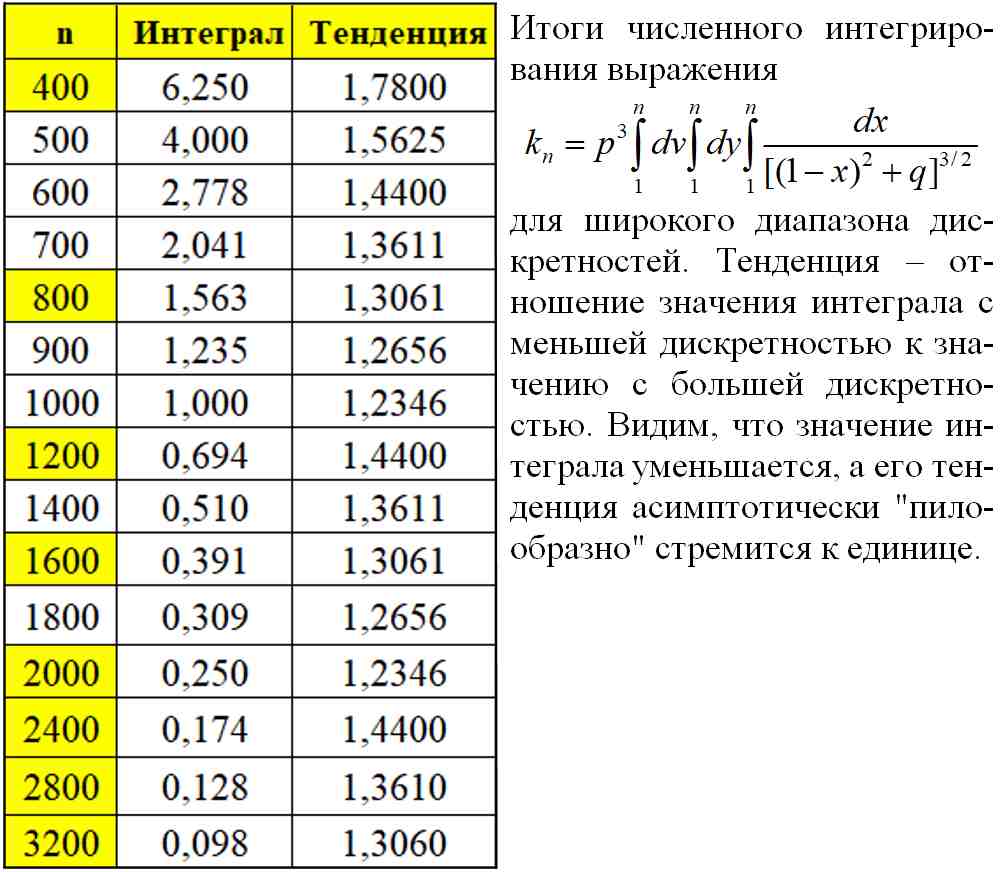
Таб.5.5. Вычисленные значения интеграла (5.7) уменьшаются, а его тенденция асимптотически "пилообразно" стремится к единице

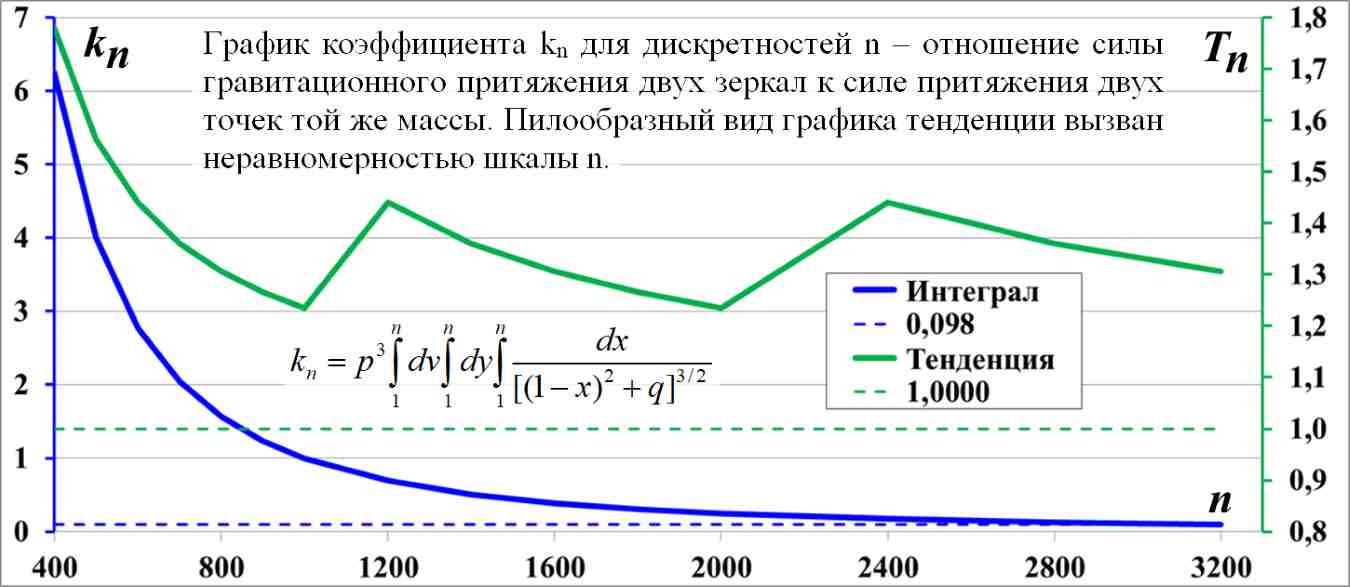
Рис.5.5. Диаграмма к таблице таб.5.5

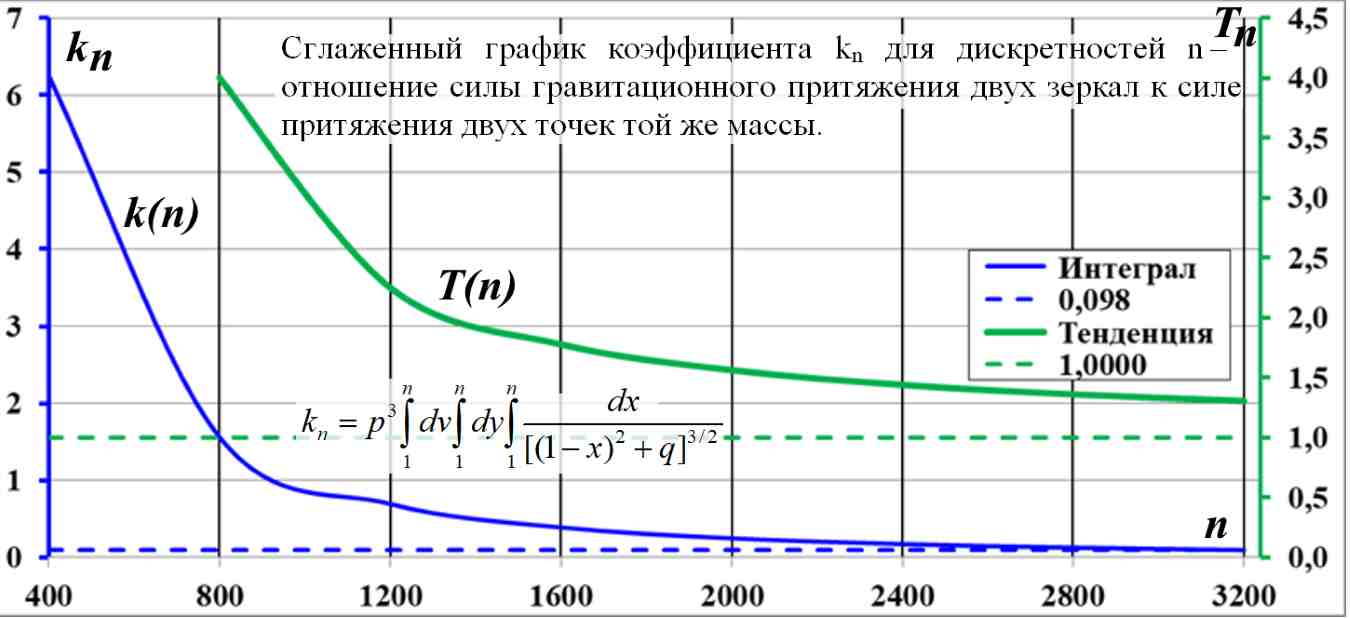
Рис.5.6. Сглаженные диаграммы к таб.5.5

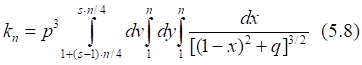
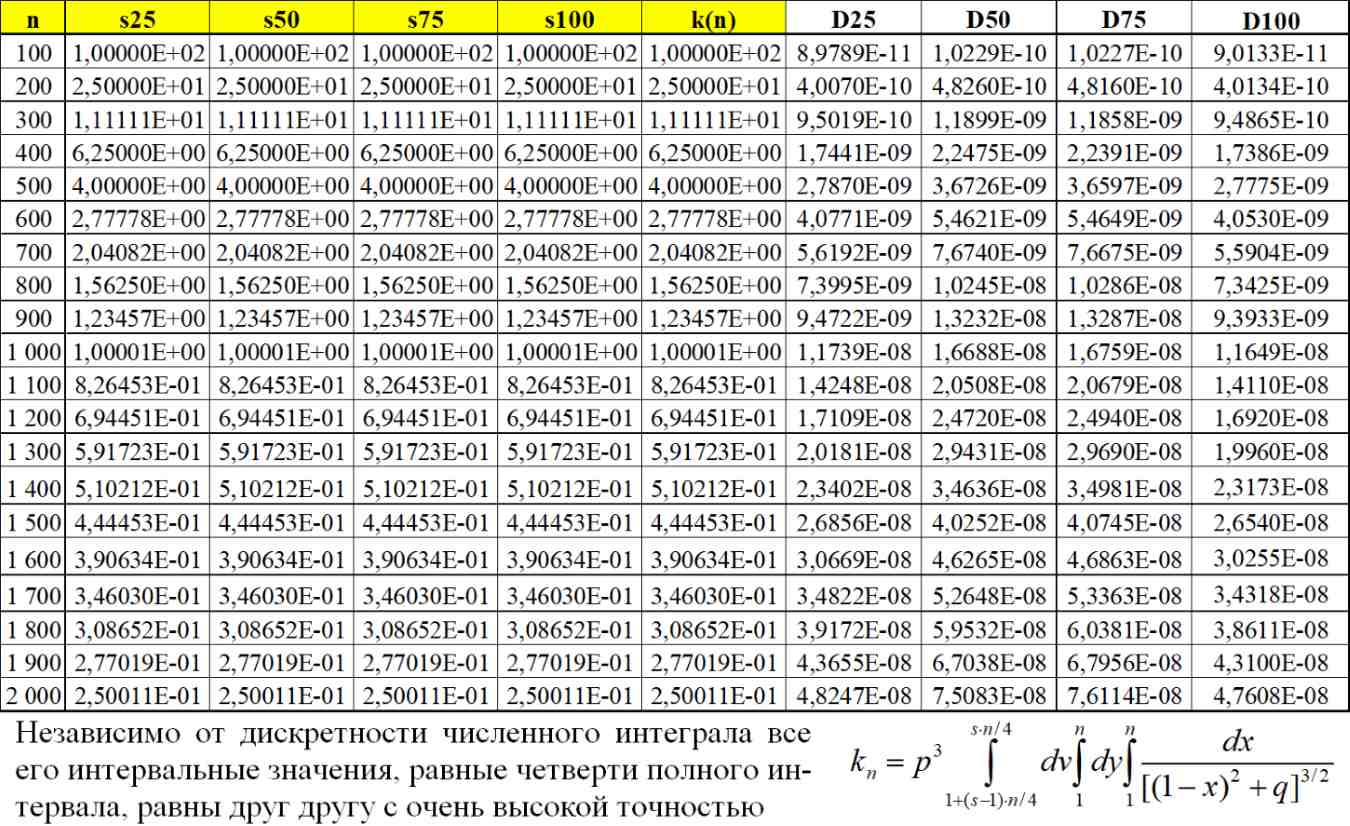
Таб.5.6. Интервальные значения интеграла (5.8) равны друг другу независимо от дискретности

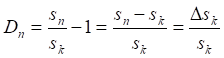
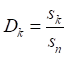
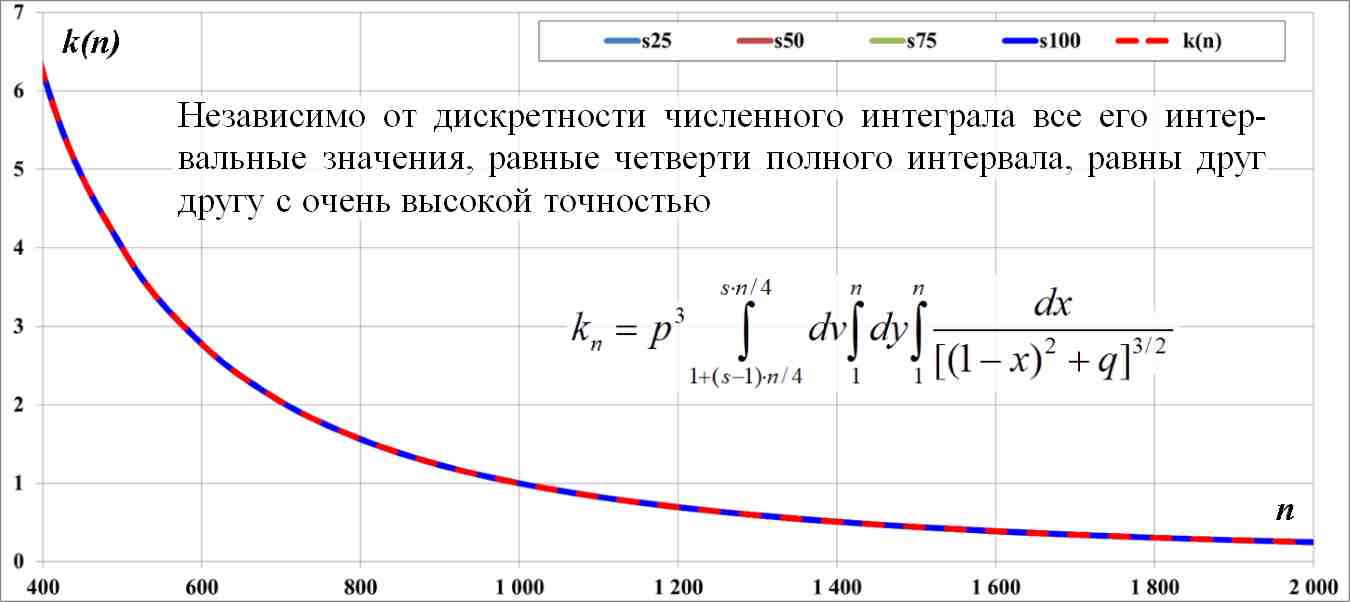
Рис.5.7. Независимо от дискретности численного интеграла (5.8) все его интервальные значения равны друг другу

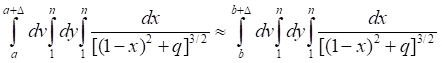
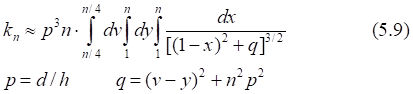
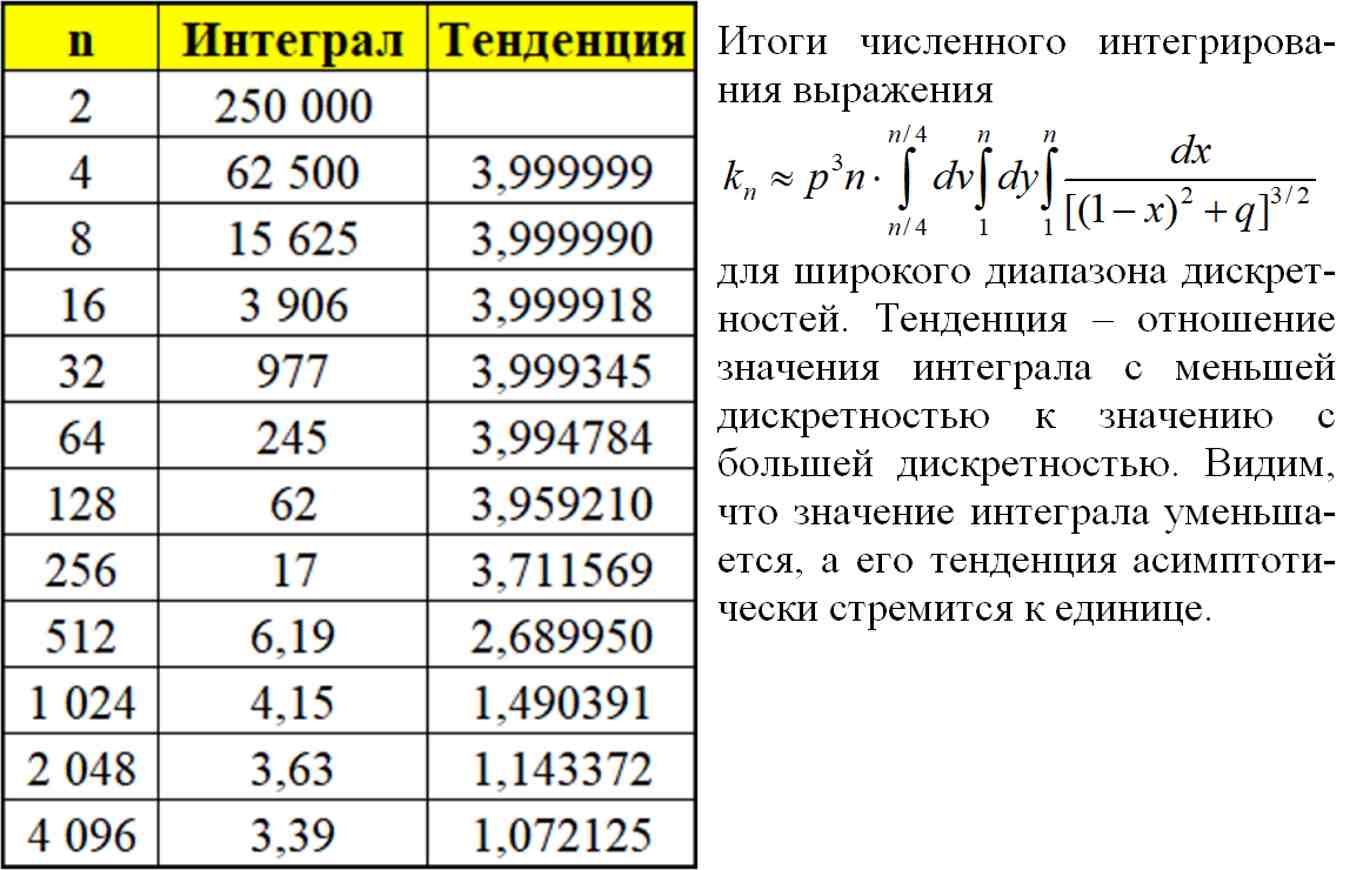
Таб.5.7. Вычисленные значения числового интеграла (5.9) уменьшаются, а его тенденция асимптотически стремится к единице.

Рис.5.8. Графики интеграла и тенденции, полученные числовым интегрированием выражения (5.9). Графики асимптотически стремятся к минимальным значениям.

Рис.5.9. Начальный, растущий этап численного вычисления интеграла (5.9), до появления скачка

Рис.5.10.  В момент прохождения точки скачка интеграл (5.10) и тенденция скачкообразно меняют значения, которые в дальнейшем практически не меняются.

Таб.5.8. Таблица значений интеграла k_n для разных дискретностей n = 400...204'800 и заданных точек скачка Δ = n%.

Рис.5.11. Компиляция диаграмм значений численного интегрирования выражения k_n для дискретности n = 51'200 и заданных точек скачка Δ.

Рис.5.12. Процесс численного интегрирования выражения k_2'048 для дискретности 204'800 и c заданным значением скачка Δ = 2'048. В момент прохождения точки скачка интеграл и тенденция скачкообразно меняют значения, которые в дальнейшем практически не меняются.

Рис.5.13. При увеличении дискретности рост погрешности замедляется

Рис.5.14. При любой дискретности погрешность растёт с уменьшением величины скачка

Таб.5.9. Таблица значений коэффициента k(d), интеграла (5.10) в зависимости от скачка

Рис.5.15. Итог численного интегрирования выражения (5.10) для всего диапазона дискретностей и со значением скачка Δ = n/100. Интеграл достиг своего предельного, минимального значения.

Рис.5.16. Использование границы функции и функциональной асимптоты

Рис.6.1. Притяжение к шару точки, находящейся на удалении от его поверхности, равном радиусу шара

Таб.6.1. Притяжение к шару точки, находящейся над его поверхностью на высоте, равной радиусу шара

Рис.6.2. Диаграмма тенденции и коэффициента силы притяжения к шару точки, находящейся над его поверхностью на высоте, равной его радиусу

Таб.6.2. Притяжение к шару точки, лежащей на его поверхности

Рис.6.3. Диаграмма тенденции и силы притяжение к шару точки, лежащей на его поверхности

Таб.6.3. Притяжение к шару точки, находящейся над его поверхностью на высоте, равной пяти радиусам шара

Рис.6.4. Диаграмма тенденции и коэффициента силы притяжение к шару точки, находящейся над его поверхностью на высоте, равной пяти его радиусам

Рис.6.5. Притяжение к шару справа точки, являющейся центром другого шара (слева) и находящейся на некотором удалении от его поверхности

Рис.7.1. Расчёт силы гравитационного притяжения двух дисков

Таб.7.1. Таблица численного интегрирования выражения (7.4)

Рис.7.2. Итоги численного вычисления интеграла (7.5).

Рис.7.3. Определение силы гравитационного притяжения точки к диску

Рис.7.4. Сравнение численным интегрированием силы притяжения диск-точка и двух точек

Рис.7.5. Притяжение к диску точки, находящейся над плоскостью диска на его оси

Рис.7.6. Сравнение относительной силы притяжения точки к диску

Рис.8.1. Гравитационное притяжение двух стержней

Рис.8.2. Сравнения сил притяжения стержней и точек. Аналитический и интегральный графики

Рис.8.3. Зависимость гравитационного радиуса от длины стержней

Рис.8.4. Сравнение силы гравитационного притяжения двух стержней с силой притяжения двух точек такой же массы и на таком же удалении

Рис.8.5. Сила притяжения двух параллельных стержней

Рис.8.6. Рост относительной силы притяжения двух параллельных стержней при уменьшении их длины

Рис.9.1. Сила притяжения площадки на верхнем зеркале к полоске на нижнем в зависимости от её положения

Рис.П1. Скриншот рабочего стола