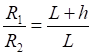
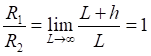
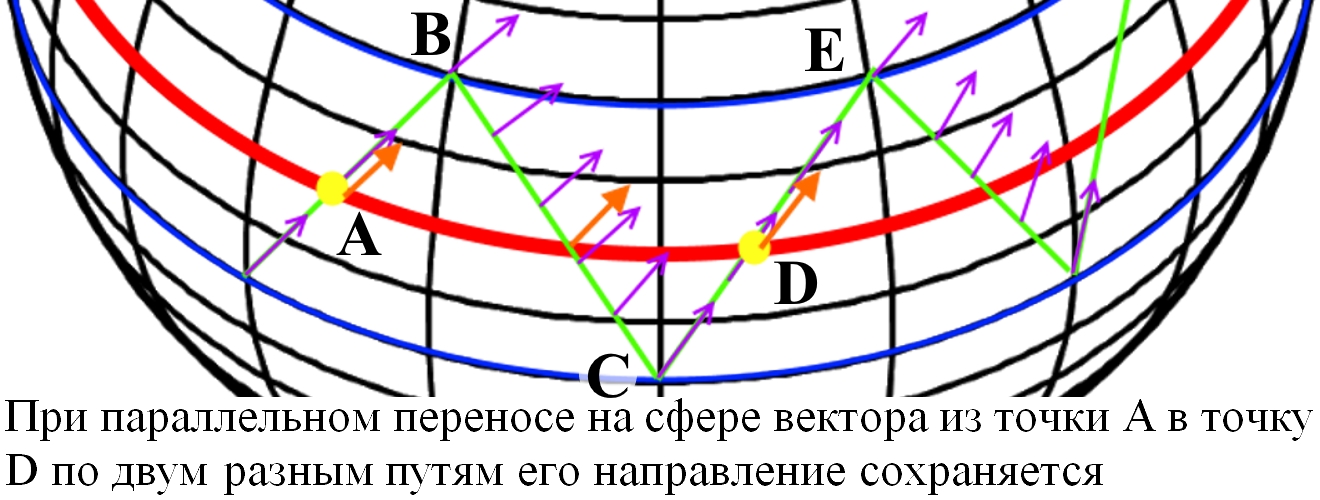
Рис.1.
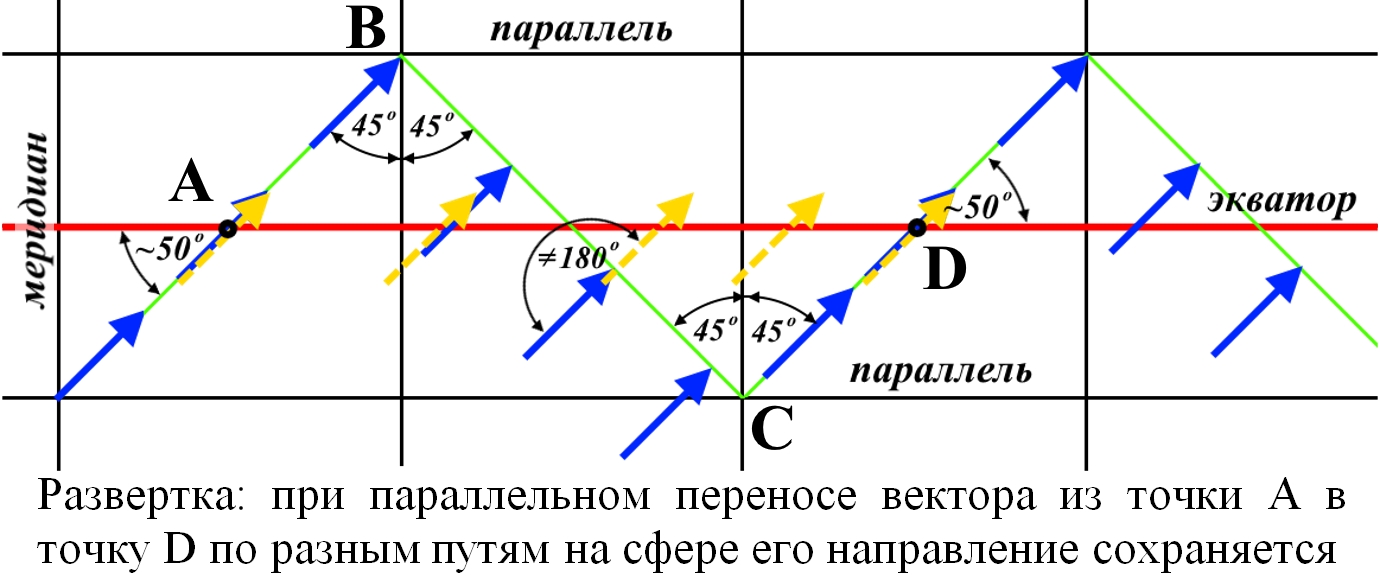
Рис.2.
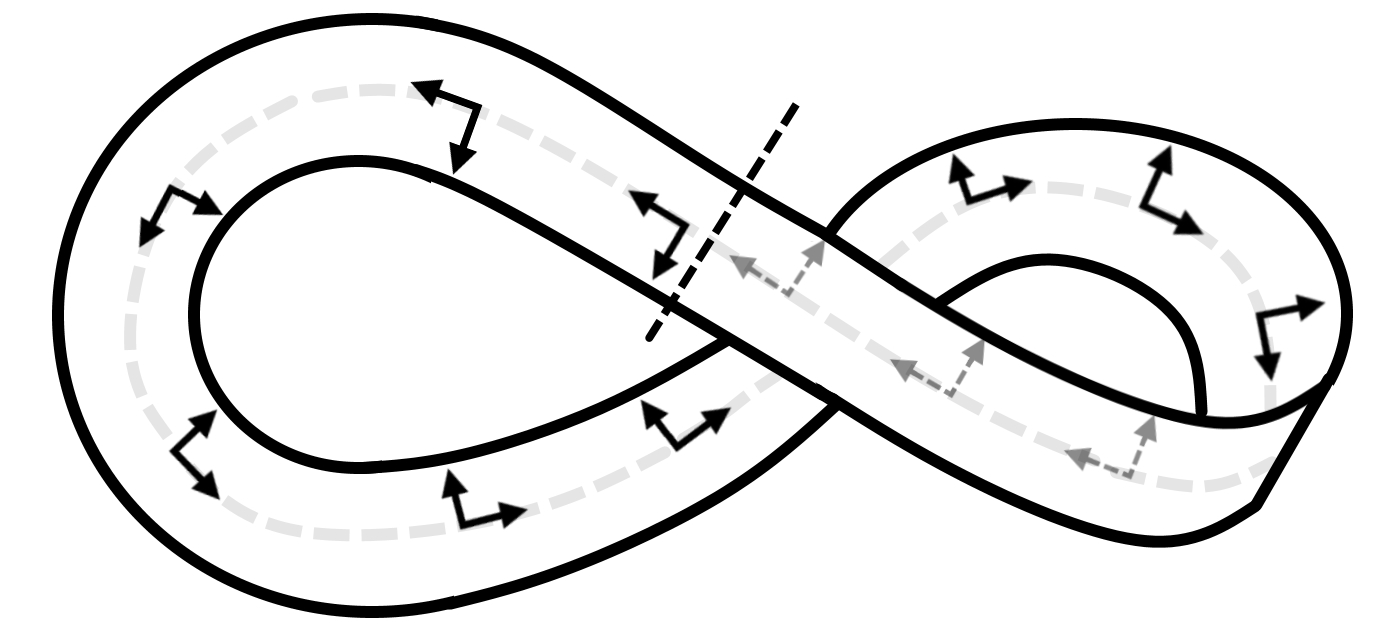
Рис.3. Рисунок 9.3 из работы [5, с.195]
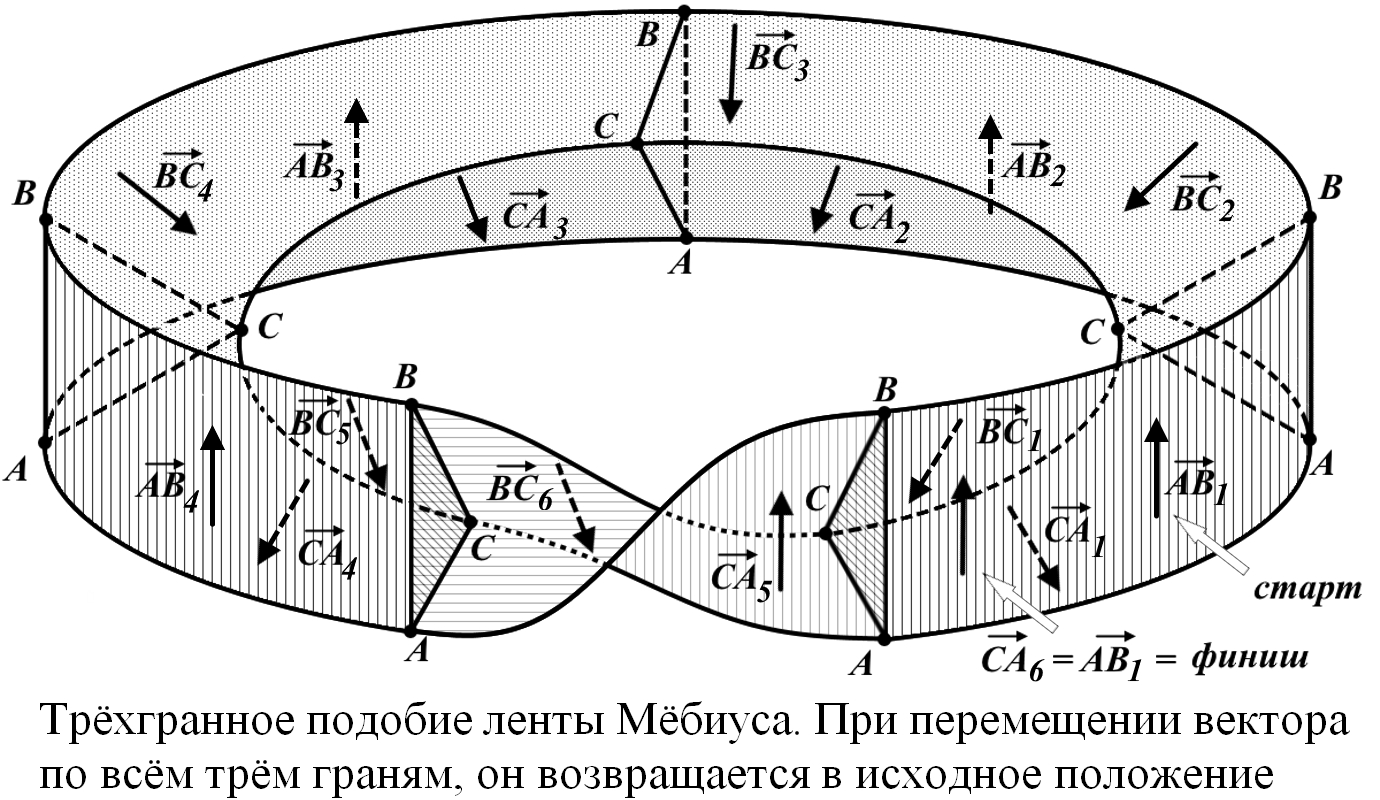
Рис.4.
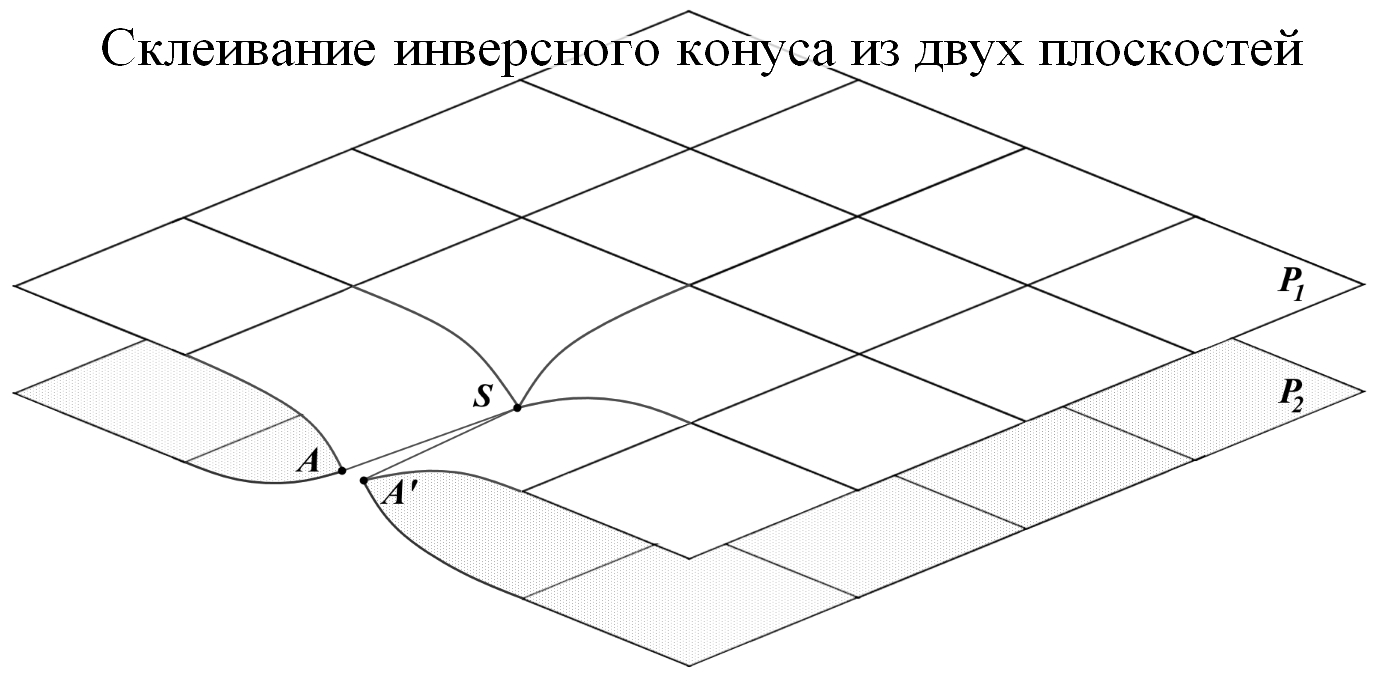
Рис.5.
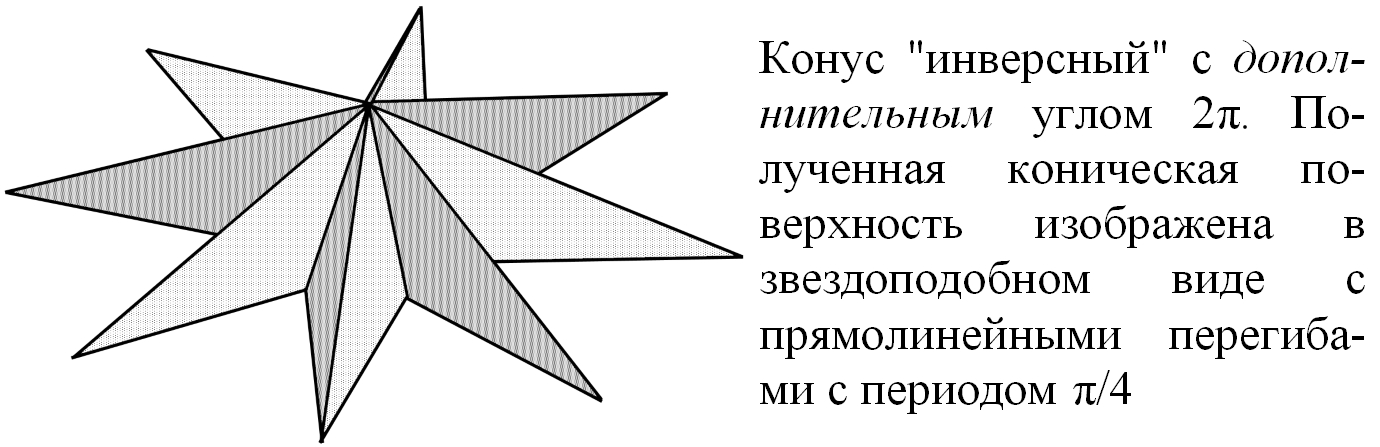
Рис.6.
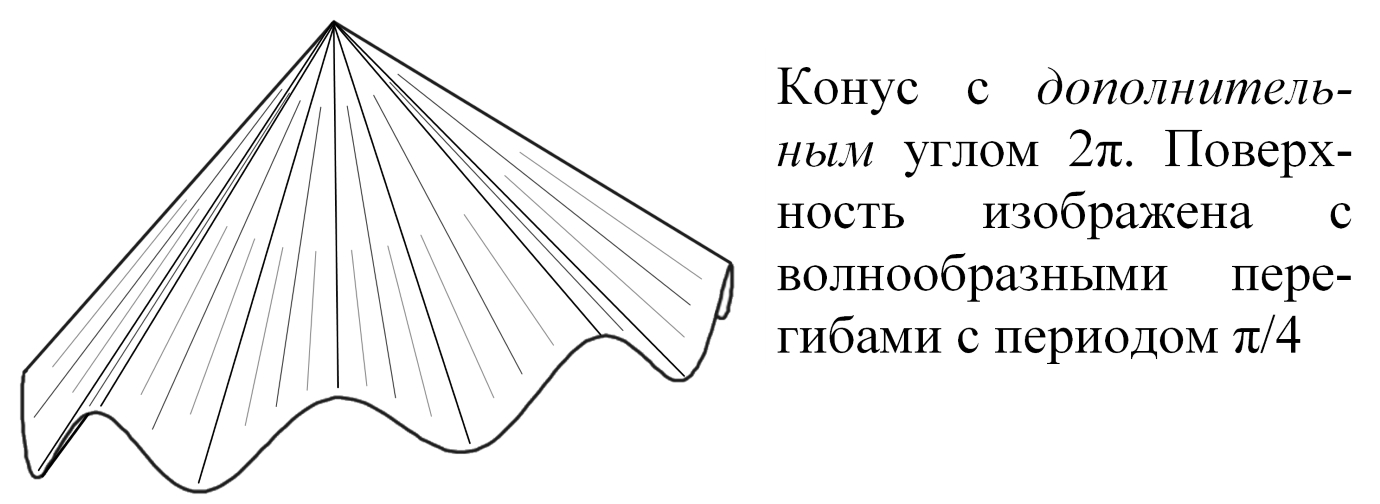
Рис.7
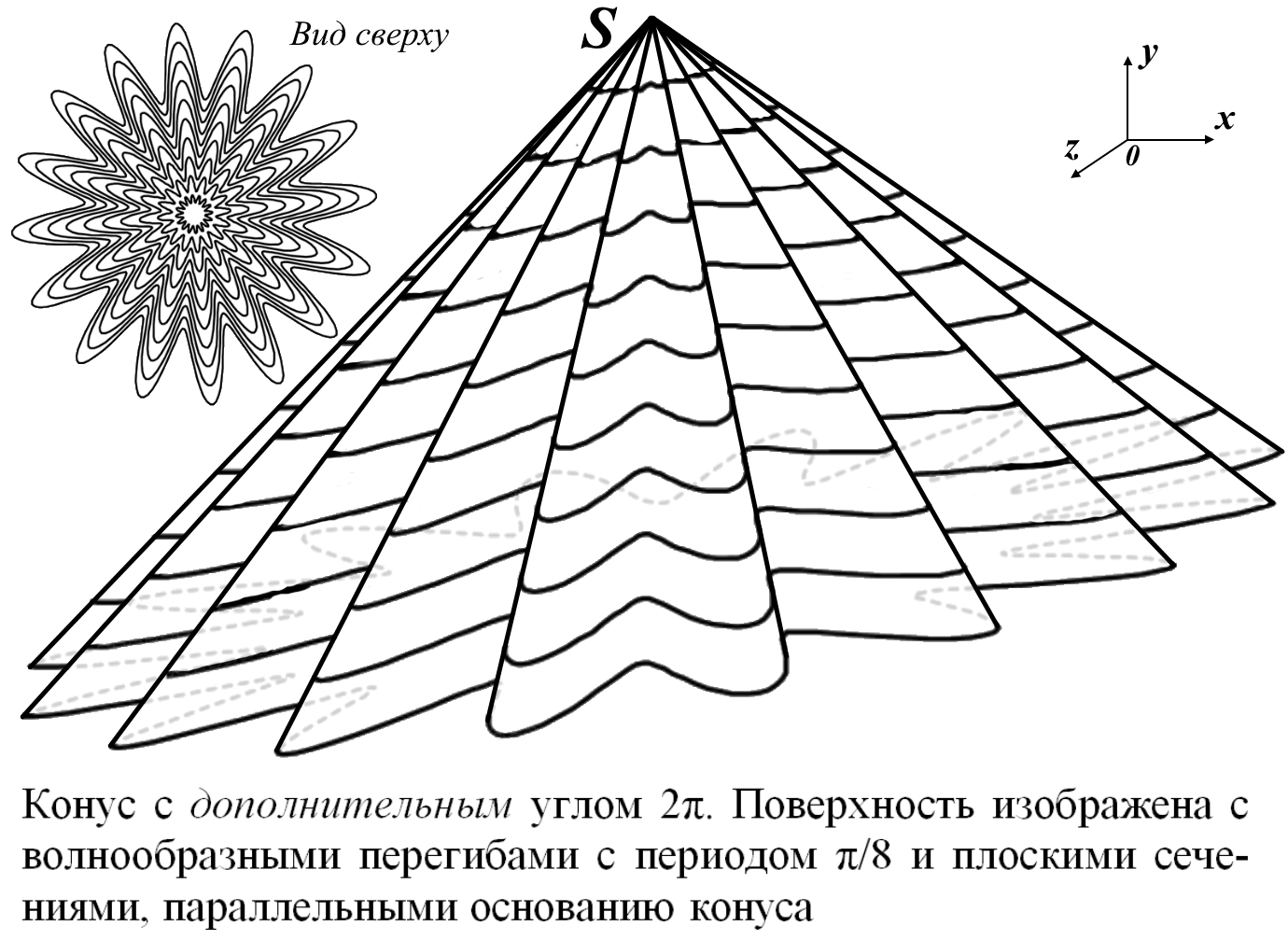
Рис.8.
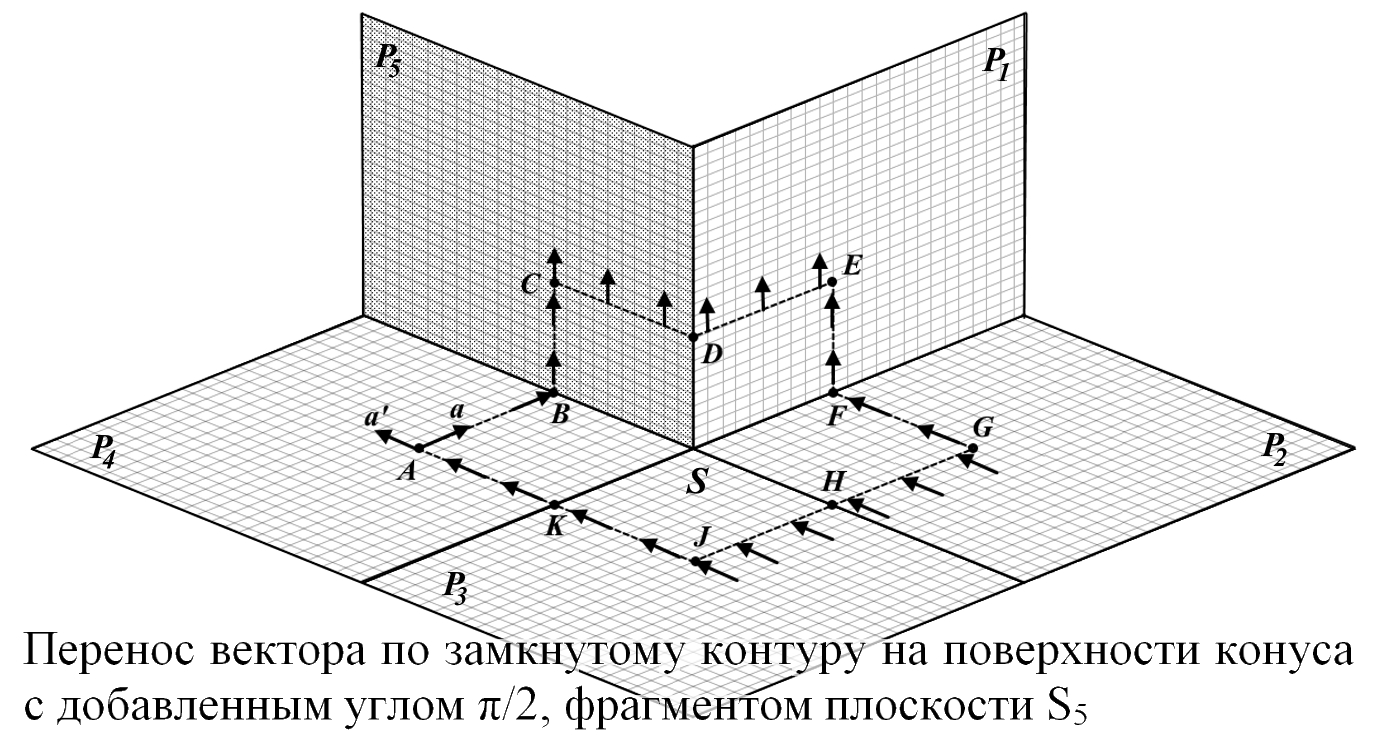
Рис.9.
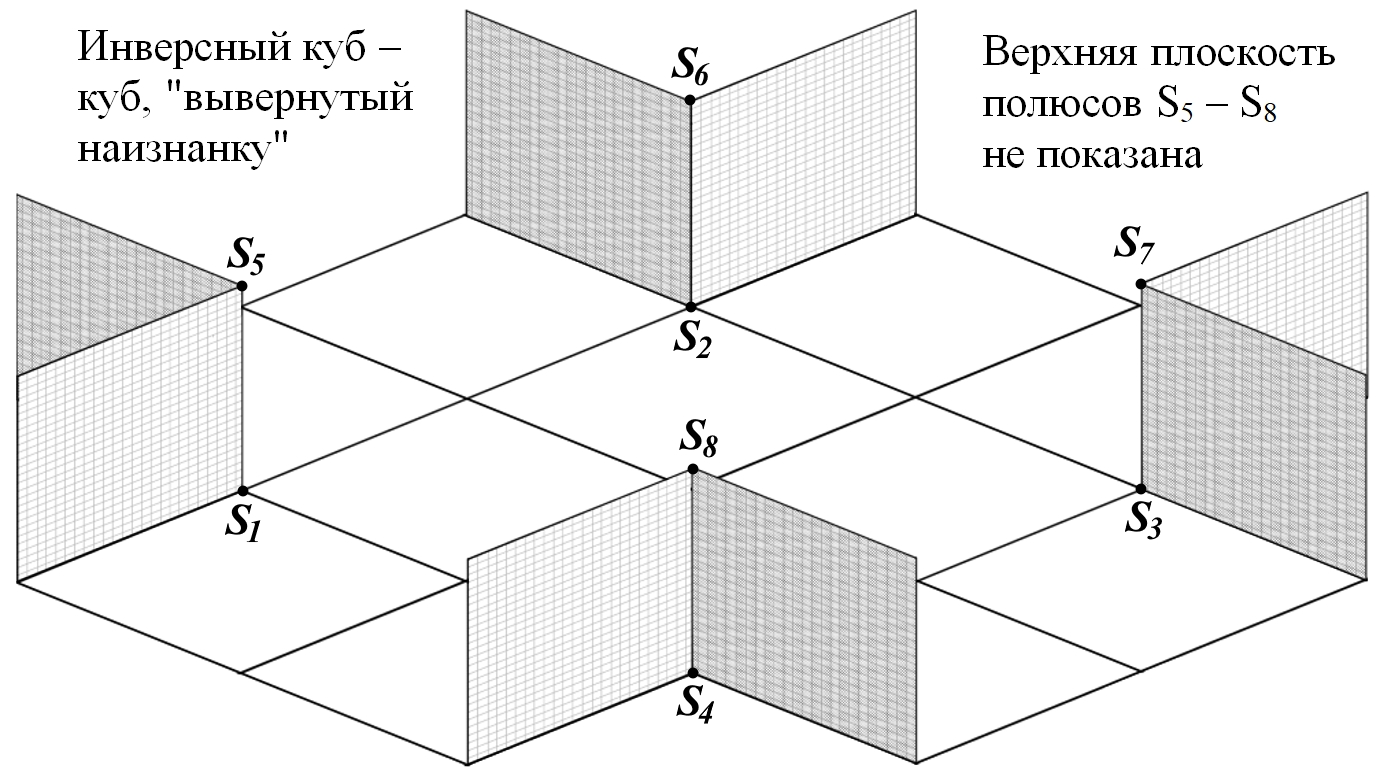
Рис.10.
14.08 - 26.09.2021
|
| |
|
Конус формируется из плоскости с вырезанным "дефицитным" углом. Если вместо вырезания добавить к плоскости клин, то при сворачивании образуется конус инверсный. Конус можно рассматривать как производную поверхность для некоторых геометрических тел с плоской поверхностью, в том числе, инверсных. Считается, что параллельный перенос вектора в 2-мерном пространстве является индикатором его искривлённости. В искривлённом пространстве перенос вектора по разным путям или по замкнутой траектории приводит к изменению его направления. Это утверждение в общем случае ошибочно. The cone is formed from a plane with a "deficient" corner cut out. If, instead of cutting, add a wedge to the plane, then an inverse cone is formed during folding. A cone can be considered as a derived surface for some geometric bodies with a flat surface, including inverse ones. It is believed that in a curved space the parallel transfer of a vector leads to a change in its direction. This assertion in the general case is erroneous. | |
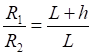
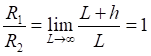

Рис.1.

Рис.2.

Рис.3. Рисунок 9.3 из работы [5, с.195]

Рис.4.

Рис.5.

Рис.6.

Рис.7

Рис.8.

Рис.9.

Рис.10.
14.08 - 26.09.2021
|
|